苏科版物理九年级上册课课练:11.5 机械效率 第1课时 机械效率的概念及简单计算(含答案)
文档属性
| 名称 | 苏科版物理九年级上册课课练:11.5 机械效率 第1课时 机械效率的概念及简单计算(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 156.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-24 00:00:00 | ||
图片预览



文档简介
[第十一章 五、 机械效率 第1课时 机械效率的概念及简单计算]
一、选择题
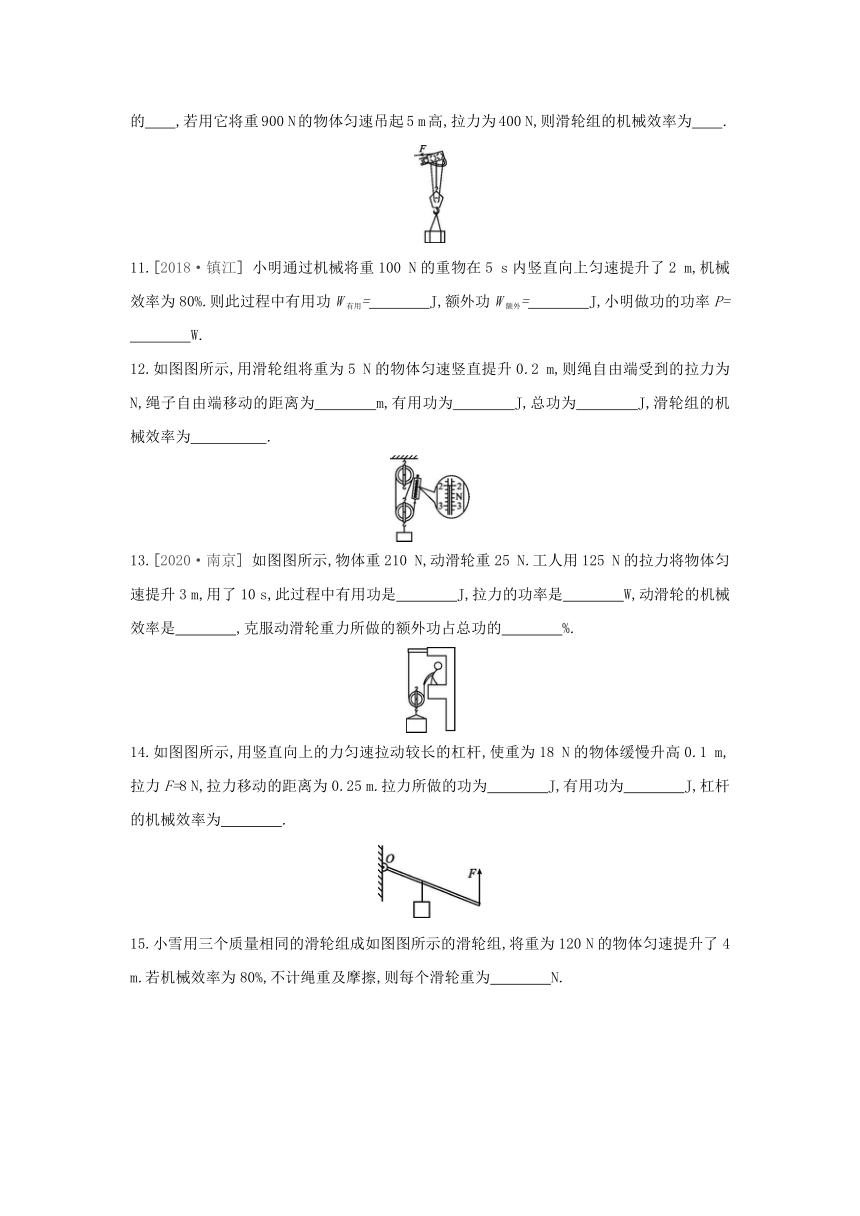
1.如图图所示,陈明同学用滑轮组提升摩托车的过程中,所做的有用功是 ( )
A.克服滑轮摩擦所做的功 B.克服摩托车重力所做的功
C.克服摩托车重力和动滑轮重力所做的功 D.克服绳子的重力所做的功
2.下列关于机械效率的说法中正确的是 ( )
A.越省力的机械,机械效率越高
B.做功越少的机械,机械效率越低
C.做功越慢的机械,机械效率越低
D.总功相同,所做有用功越多的机械,机械效率越高
3.甲、乙两种机械的效率分别是70%和50%,下列说法中正确的是 ( )
A.使用甲机械省力
B.使用甲机械做功快
C.在相同的时间内,使用甲机械完成的功多
D.使用乙机械所做的额外功在总功中占的比例大
4.小文同学采用如图图所示的两种不同的方式将同一货物搬运到同一辆汽车上,下列说法中正确的是 ( )
A.甲种方法对货物做功比较多 B.乙种方法更省力
C.两种方法机械效率相等 D.两种情况下,甲的机械效率小于乙的机械效率
5.[2019·南通] 如图图所示,用滑轮组将重为12 N的物体匀速提升0.2 m,作用在绳端的拉力F为5 N,不计绳重和摩擦.利用以上信息不能求解的物理量是 ( )
A.拉力的功率 B.动滑轮的重力
C.滑轮组的额外功 D.滑轮组的机械效率
6.[2020-2021学年靖江市校级期中] 如图图所示,重12 N的物体G在竖直向上、大小为8 N的拉力F的作用下上升了0.2 m,绳子自由端移动的速度是0.1 m/s.这一过程中,能得到的结论是 ( )
A.力F做功的时间为2 s
B.该动滑轮的机械效率为80%
C.克服动滑轮重力所做的额外功一定小于0.8 J
D.拉力F做功的功率为0.4 W
7.如图图所示,在大小为150 N的拉力F作用下,物体A在水平桌面上以0.2 m/s的速度向右匀速运动了2 m,已知A的重力为2000 N,桌面对A的摩擦力为360 N,则下列说法中正确的是 ( )
A.有用功为4000 J
B.拉力做的功为90 J
C.滑轮组的机械效率为80%
D.拉力做功的功率为30 W
二、填空题
8.利用机械工作时,因为额外功是不可避免的,故总功总是 有用功,所以机械效率总是 1.(均选填“大于”“小于”或“等于”)
9.某人从深为5 m的井中直接将一桶水提出井口,已知桶重20 N,桶中水重80 N.若此人的目的是提水,则有用功为 ,总功为 ,额外功为 ,机械效率为 ;若此人的目的是捞桶,则有用功为 ,总功为 ,额外功为 ,机械效率为 .
10.[2020·徐州] 如图图所示,塔式起重机上的滑轮组既可以 ,又可以改变施力的 ,若用它将重900 N的物体匀速吊起5 m高,拉力为400 N,则滑轮组的机械效率为 .
11.[2018·镇江] 小明通过机械将重100 N的重物在5 s内竖直向上匀速提升了2 m,机械效率为80%.则此过程中有用功W有用= J,额外功W额外= J,小明做功的功率P=
W.
12.如图图所示,用滑轮组将重为5 N的物体匀速竖直提升0.2 m,则绳自由端受到的拉力为 N,绳子自由端移动的距离为 m,有用功为 J,总功为 J,滑轮组的机械效率为 .
13.[2020·南京] 如图图所示,物体重210 N,动滑轮重25 N.工人用125 N的拉力将物体匀速提升3 m,用了10 s,此过程中有用功是 J,拉力的功率是 W,动滑轮的机械效率是 ,克服动滑轮重力所做的额外功占总功的 %.
14.如图图所示,用竖直向上的力匀速拉动较长的杠杆,使重为18 N的物体缓慢升高0.1 m,拉力F=8 N,拉力移动的距离为0.25 m.拉力所做的功为 J,有用功为 J,杠杆的机械效率为 .
15.小雪用三个质量相同的滑轮组成如图图所示的滑轮组,将重为120 N的物体匀速提升了4 m.若机械效率为80%,不计绳重及摩擦,则每个滑轮重为 N.
三、解答题
16.[2020·泰州] 小明利用如图图所示的滑轮组,将质量为90 kg的物体在1 min内匀速提升5 m,竖直向上的拉力为360 N.求:(g取10 N/kg)
(1)物体的重力.
(2)拉力做功的功率.
(3)滑轮组的机械效率.
17.[2020·南通] 如图图所示,塔式起重机上的滑轮组将重为1.2×104 N的重物匀速吊起2 m时,滑轮组的机械效率为80%,g取10 N/kg.
(1)求提升重物做的有用功.
(2)求绳端的拉力.
(3)若动滑轮的质量为40 kg,求克服摩擦力和钢丝绳重力所做的功.
18.一名建筑工人要把建筑材料运送到楼上,他使用了如图图所示的装置进行升降,已知吊篮的质量为m1,建筑材料的质量为m2,人对绳子的拉力为F,吊篮在拉力的作用下匀速上升了h,不计绳重和摩擦.下列表述正确的是 ( )
A.有用功为m2 gh,动滑轮的重力为2F-(m1+m2)g
B.有用功为m2 gh,滑轮组的机械效率为×100%
C.有用功为(m1+m2)gh,滑轮组的机械效率为×100%
D.额外功为(2F-m1 g-m2 g)h,绳端移动的距离为2h
答案
1.B 有用功是对人们有用的功,用滑轮组提升摩托车的过程中,目的是将摩托车提升到高处,故克服摩托车重力所做的功就是有用功.
2.D
3.D 机械效率高是指做的功中有用功占总功的比例大,与使用机械是否省力无关,故A错误;功率是表示做功快慢的物理量,而功率与机械效率没有必然的联系,故B错误;机械效率高是指做的功中有用功占总功的比例大,与做功的多少无关,故C错误;乙的机械效率较低,说明使用乙机械做功时,有用功占总功的比例小,额外功占总功的比例大,故D正确.
4.D 根据W=Gh可知,不管用哪种方法,克服货物重力做的功,即对货物做的功都是一样的,故A错误;乙方法是直接搬货物,所以人用的力就等于货物的重力,甲方法是利用斜面来搬运货物,而斜面是省力、费距离的一种机械,故甲方法更省力,故B错误;机械效率是有用功占总功的比值,而使用机械(甲方法中的斜面就是一种机械)与不使用机械(乙方法)相比,多了机械带来的额外功,所以甲方法的机械效率较低,故C错误;由C项的分析可知,甲的机械效率比乙低,故D正确.
5.A 绳端移动的距离:s=nh=3×0.2 m=0.6 m,拉力做的功:W总=Fs=5 N×0.6 m=3 J,由于没有做功时间,则不能求解拉力的功率,故A符合题意;不计绳重和摩擦,拉力F=(G+G动),动滑轮的重力:G动=3F-G=3×5 N-12 N=3 N,故B不符合题意;有用功:W有用=Gh=12 N×0.2 m=2.4 J,额外功:W额外=W总-W有用=3 J-2.4 J=0.6 J,故C不符合题意;滑轮组的机械效率:η=×100%=×100%=80%,故D不符合题意.
6.C 由图知,n=2.
绳端移动的距离:s=nh=2×0.2 m=0.4 m,由v=可得,力F做功的时间:t===4 s,故A错误;
拉力做的总功:W总=Fs=8 N×0.4 m=3.2 J,有用功:W有用=Gh=12 N×0.2 m=2.4 J,则动滑轮的机械效率:η=×100%=×100%=75%,故B错误;
额外功W额外=W总-W有用=3.2 J-2.4 J=0.8 J,因实际上需要克服摩擦和绳重做一部分额外功,所以克服动滑轮重力所做的额外功一定小于0.8 J,故C正确;
拉力F做功的功率:P===0.8 W,故D错误.
7.C
8.大于 小于
9.400 J 500 J 100 J 80% 100 J 500 J 400 J 20%
为了提水,则对水做的功为有用功,对桶做的功为额外功.W有用=G水h=80 N×5 m=400 J,W额外=G桶h=20 N×5 m=100 J,则W总=W有用+W额外=500 J,η=×100%=×100%=80%.为了捞桶,则对桶做的功为有用功,对水做的功为额外功.W有用'=G桶h=20 N×5 m=100 J,W额外'=G水h=80 N×5 m=400 J,W总'=W有用'+W额外'=100 J+400 J=500 J,则η'=×100%=×100%=20%.
10.省力 方向 75% (1)在图中的滑轮组中,使用下面的动滑轮可以省力,使用上面的定滑轮可以改变用力的方向,所以使用图中的滑轮组,既可以省力,也可以改变施力的方向.
(2)拉力做的有用功:
W有用=Gh=900 N×5 m=4500 J;
由图知,承担物重的绳子段数n=3,拉力端移动的距离:s=3h=3×5 m=15 m,
拉力做的总功:
W总=Fs=400 N×15 m=6000 J,
滑轮组的机械效率:
η=×100%=×100%=75%.
11.200 50 50 此过程中有用功:W有用=Gh=100 N×2 m=200 J;根据η=×100%可知,总功:W总===250 J;额外功:W额外=W总-W有用=250 J-200 J=50 J;小明做功的功率:P===50 W.
12.2 0.6 1 1.2 83.3%
本题装置中承重的绳子段数为3,所以绳自由端移动的距离为物体上升高度的3倍,即s=3h=3×0.2 m=0.6 m.有用功为克服物体重力做的功,W有用=Gh=5 N×0.2 m=1 J,拉力做的总功为W总=Fs=2 N×0.6 m=1.2 J,所以机械效率:η=×100%=×100%≈83.3%.
13.630 75 84% 10 (1)拉力做的有用功:W有用=Gh=210 N×3 m=630 J.
(2)由图知,n=2,拉力端移动的距离:s=2h=2×3 m=6 m,拉力做的总功:
W总=Fs=125 N×6 m=750 J,
拉力做功的功率:P===75 W.
(3)动滑轮的机械效率:η=×100%=×100%=84%.
(4)提升动滑轮做的额外功:
W额1=G动h=25 N×3 m=75 J,
克服动滑轮重力所做的额外功占总功的比例:η'===0.1=10%.
14.2 1.8 90%
有用功为克服物体重力做的功,W有用=Gh=18 N×0.1 m=1.8 J;拉力做的总功为W总=Fs=8 N×0.25 m=2 J;所以机械效率η=×100%=×100%=90%.
15.30 由题图知,n=3,η=×100%=×100%=×100%,则F===50 N;不计绳重和摩擦,F=,即50 N=,则G动=30 N.
16.(1)物体的重力:
G=mg=90 kg×10 N/kg=900 N.
(2)由图知,n=3,
拉力端移动的距离:s=3h=3×5 m=15 m,
拉力做的总功:W总=Fs=360 N×15 m=5400 J,
拉力做功的功率:P===90 W.
(3)拉力做的有用功:W有用=Gh=900 N×5 m=4500 J,
滑轮组的机械效率:η=×100%=×100%≈83.3%.
17.(1)提升重物做的有用功:W有用=Gh=1.2×104 N×2 m=2.4×104 J.
(2)由η=×100%可得,拉力做的总功:W总===3×104 J;由图可知,n=3,绳子自由端移动的距离:s=nh=3×2 m=6 m;由W=Fs可得,拉力F===5000 N.
(3)克服动滑轮重力、摩擦力和钢丝绳重力所做的额外功:W额外=W总-W有用=3×104 J-2.4×104 J=6000 J,提升动滑轮做的额外功:W额1=G动h=m动gh=40 kg×10 N/kg×2 m=800 J,克服摩擦力和钢丝绳重力所做的额外功:W额2=W额外-W额1=6000 J-800 J=5200 J.
18.A 由图知作用在动滑轮上的绳子有2段,则绳端移动的距离为2h,
有用功为W有用=Gh=m2gh,
总功为W总=Fs=F·2h=2Fh,
机械效率为η=×100%=×100%=×100%;
额外功为W额外=W总-W有用=2Fh-m2 gh=(2F-m2g)h,
对吊篮做的功为W1=G1h=m1gh,
对动滑轮做的功为W动=W额外-W1=(2F-m2g)h-m1gh=(2F-m2g-m1g)h;
动滑轮的重力为G动===2F-(m1+m2)g.
一、选择题
1.如图图所示,陈明同学用滑轮组提升摩托车的过程中,所做的有用功是 ( )
A.克服滑轮摩擦所做的功 B.克服摩托车重力所做的功
C.克服摩托车重力和动滑轮重力所做的功 D.克服绳子的重力所做的功
2.下列关于机械效率的说法中正确的是 ( )
A.越省力的机械,机械效率越高
B.做功越少的机械,机械效率越低
C.做功越慢的机械,机械效率越低
D.总功相同,所做有用功越多的机械,机械效率越高
3.甲、乙两种机械的效率分别是70%和50%,下列说法中正确的是 ( )
A.使用甲机械省力
B.使用甲机械做功快
C.在相同的时间内,使用甲机械完成的功多
D.使用乙机械所做的额外功在总功中占的比例大
4.小文同学采用如图图所示的两种不同的方式将同一货物搬运到同一辆汽车上,下列说法中正确的是 ( )
A.甲种方法对货物做功比较多 B.乙种方法更省力
C.两种方法机械效率相等 D.两种情况下,甲的机械效率小于乙的机械效率
5.[2019·南通] 如图图所示,用滑轮组将重为12 N的物体匀速提升0.2 m,作用在绳端的拉力F为5 N,不计绳重和摩擦.利用以上信息不能求解的物理量是 ( )
A.拉力的功率 B.动滑轮的重力
C.滑轮组的额外功 D.滑轮组的机械效率
6.[2020-2021学年靖江市校级期中] 如图图所示,重12 N的物体G在竖直向上、大小为8 N的拉力F的作用下上升了0.2 m,绳子自由端移动的速度是0.1 m/s.这一过程中,能得到的结论是 ( )
A.力F做功的时间为2 s
B.该动滑轮的机械效率为80%
C.克服动滑轮重力所做的额外功一定小于0.8 J
D.拉力F做功的功率为0.4 W
7.如图图所示,在大小为150 N的拉力F作用下,物体A在水平桌面上以0.2 m/s的速度向右匀速运动了2 m,已知A的重力为2000 N,桌面对A的摩擦力为360 N,则下列说法中正确的是 ( )
A.有用功为4000 J
B.拉力做的功为90 J
C.滑轮组的机械效率为80%
D.拉力做功的功率为30 W
二、填空题
8.利用机械工作时,因为额外功是不可避免的,故总功总是 有用功,所以机械效率总是 1.(均选填“大于”“小于”或“等于”)
9.某人从深为5 m的井中直接将一桶水提出井口,已知桶重20 N,桶中水重80 N.若此人的目的是提水,则有用功为 ,总功为 ,额外功为 ,机械效率为 ;若此人的目的是捞桶,则有用功为 ,总功为 ,额外功为 ,机械效率为 .
10.[2020·徐州] 如图图所示,塔式起重机上的滑轮组既可以 ,又可以改变施力的 ,若用它将重900 N的物体匀速吊起5 m高,拉力为400 N,则滑轮组的机械效率为 .
11.[2018·镇江] 小明通过机械将重100 N的重物在5 s内竖直向上匀速提升了2 m,机械效率为80%.则此过程中有用功W有用= J,额外功W额外= J,小明做功的功率P=
W.
12.如图图所示,用滑轮组将重为5 N的物体匀速竖直提升0.2 m,则绳自由端受到的拉力为 N,绳子自由端移动的距离为 m,有用功为 J,总功为 J,滑轮组的机械效率为 .
13.[2020·南京] 如图图所示,物体重210 N,动滑轮重25 N.工人用125 N的拉力将物体匀速提升3 m,用了10 s,此过程中有用功是 J,拉力的功率是 W,动滑轮的机械效率是 ,克服动滑轮重力所做的额外功占总功的 %.
14.如图图所示,用竖直向上的力匀速拉动较长的杠杆,使重为18 N的物体缓慢升高0.1 m,拉力F=8 N,拉力移动的距离为0.25 m.拉力所做的功为 J,有用功为 J,杠杆的机械效率为 .
15.小雪用三个质量相同的滑轮组成如图图所示的滑轮组,将重为120 N的物体匀速提升了4 m.若机械效率为80%,不计绳重及摩擦,则每个滑轮重为 N.
三、解答题
16.[2020·泰州] 小明利用如图图所示的滑轮组,将质量为90 kg的物体在1 min内匀速提升5 m,竖直向上的拉力为360 N.求:(g取10 N/kg)
(1)物体的重力.
(2)拉力做功的功率.
(3)滑轮组的机械效率.
17.[2020·南通] 如图图所示,塔式起重机上的滑轮组将重为1.2×104 N的重物匀速吊起2 m时,滑轮组的机械效率为80%,g取10 N/kg.
(1)求提升重物做的有用功.
(2)求绳端的拉力.
(3)若动滑轮的质量为40 kg,求克服摩擦力和钢丝绳重力所做的功.
18.一名建筑工人要把建筑材料运送到楼上,他使用了如图图所示的装置进行升降,已知吊篮的质量为m1,建筑材料的质量为m2,人对绳子的拉力为F,吊篮在拉力的作用下匀速上升了h,不计绳重和摩擦.下列表述正确的是 ( )
A.有用功为m2 gh,动滑轮的重力为2F-(m1+m2)g
B.有用功为m2 gh,滑轮组的机械效率为×100%
C.有用功为(m1+m2)gh,滑轮组的机械效率为×100%
D.额外功为(2F-m1 g-m2 g)h,绳端移动的距离为2h
答案
1.B 有用功是对人们有用的功,用滑轮组提升摩托车的过程中,目的是将摩托车提升到高处,故克服摩托车重力所做的功就是有用功.
2.D
3.D 机械效率高是指做的功中有用功占总功的比例大,与使用机械是否省力无关,故A错误;功率是表示做功快慢的物理量,而功率与机械效率没有必然的联系,故B错误;机械效率高是指做的功中有用功占总功的比例大,与做功的多少无关,故C错误;乙的机械效率较低,说明使用乙机械做功时,有用功占总功的比例小,额外功占总功的比例大,故D正确.
4.D 根据W=Gh可知,不管用哪种方法,克服货物重力做的功,即对货物做的功都是一样的,故A错误;乙方法是直接搬货物,所以人用的力就等于货物的重力,甲方法是利用斜面来搬运货物,而斜面是省力、费距离的一种机械,故甲方法更省力,故B错误;机械效率是有用功占总功的比值,而使用机械(甲方法中的斜面就是一种机械)与不使用机械(乙方法)相比,多了机械带来的额外功,所以甲方法的机械效率较低,故C错误;由C项的分析可知,甲的机械效率比乙低,故D正确.
5.A 绳端移动的距离:s=nh=3×0.2 m=0.6 m,拉力做的功:W总=Fs=5 N×0.6 m=3 J,由于没有做功时间,则不能求解拉力的功率,故A符合题意;不计绳重和摩擦,拉力F=(G+G动),动滑轮的重力:G动=3F-G=3×5 N-12 N=3 N,故B不符合题意;有用功:W有用=Gh=12 N×0.2 m=2.4 J,额外功:W额外=W总-W有用=3 J-2.4 J=0.6 J,故C不符合题意;滑轮组的机械效率:η=×100%=×100%=80%,故D不符合题意.
6.C 由图知,n=2.
绳端移动的距离:s=nh=2×0.2 m=0.4 m,由v=可得,力F做功的时间:t===4 s,故A错误;
拉力做的总功:W总=Fs=8 N×0.4 m=3.2 J,有用功:W有用=Gh=12 N×0.2 m=2.4 J,则动滑轮的机械效率:η=×100%=×100%=75%,故B错误;
额外功W额外=W总-W有用=3.2 J-2.4 J=0.8 J,因实际上需要克服摩擦和绳重做一部分额外功,所以克服动滑轮重力所做的额外功一定小于0.8 J,故C正确;
拉力F做功的功率:P===0.8 W,故D错误.
7.C
8.大于 小于
9.400 J 500 J 100 J 80% 100 J 500 J 400 J 20%
为了提水,则对水做的功为有用功,对桶做的功为额外功.W有用=G水h=80 N×5 m=400 J,W额外=G桶h=20 N×5 m=100 J,则W总=W有用+W额外=500 J,η=×100%=×100%=80%.为了捞桶,则对桶做的功为有用功,对水做的功为额外功.W有用'=G桶h=20 N×5 m=100 J,W额外'=G水h=80 N×5 m=400 J,W总'=W有用'+W额外'=100 J+400 J=500 J,则η'=×100%=×100%=20%.
10.省力 方向 75% (1)在图中的滑轮组中,使用下面的动滑轮可以省力,使用上面的定滑轮可以改变用力的方向,所以使用图中的滑轮组,既可以省力,也可以改变施力的方向.
(2)拉力做的有用功:
W有用=Gh=900 N×5 m=4500 J;
由图知,承担物重的绳子段数n=3,拉力端移动的距离:s=3h=3×5 m=15 m,
拉力做的总功:
W总=Fs=400 N×15 m=6000 J,
滑轮组的机械效率:
η=×100%=×100%=75%.
11.200 50 50 此过程中有用功:W有用=Gh=100 N×2 m=200 J;根据η=×100%可知,总功:W总===250 J;额外功:W额外=W总-W有用=250 J-200 J=50 J;小明做功的功率:P===50 W.
12.2 0.6 1 1.2 83.3%
本题装置中承重的绳子段数为3,所以绳自由端移动的距离为物体上升高度的3倍,即s=3h=3×0.2 m=0.6 m.有用功为克服物体重力做的功,W有用=Gh=5 N×0.2 m=1 J,拉力做的总功为W总=Fs=2 N×0.6 m=1.2 J,所以机械效率:η=×100%=×100%≈83.3%.
13.630 75 84% 10 (1)拉力做的有用功:W有用=Gh=210 N×3 m=630 J.
(2)由图知,n=2,拉力端移动的距离:s=2h=2×3 m=6 m,拉力做的总功:
W总=Fs=125 N×6 m=750 J,
拉力做功的功率:P===75 W.
(3)动滑轮的机械效率:η=×100%=×100%=84%.
(4)提升动滑轮做的额外功:
W额1=G动h=25 N×3 m=75 J,
克服动滑轮重力所做的额外功占总功的比例:η'===0.1=10%.
14.2 1.8 90%
有用功为克服物体重力做的功,W有用=Gh=18 N×0.1 m=1.8 J;拉力做的总功为W总=Fs=8 N×0.25 m=2 J;所以机械效率η=×100%=×100%=90%.
15.30 由题图知,n=3,η=×100%=×100%=×100%,则F===50 N;不计绳重和摩擦,F=,即50 N=,则G动=30 N.
16.(1)物体的重力:
G=mg=90 kg×10 N/kg=900 N.
(2)由图知,n=3,
拉力端移动的距离:s=3h=3×5 m=15 m,
拉力做的总功:W总=Fs=360 N×15 m=5400 J,
拉力做功的功率:P===90 W.
(3)拉力做的有用功:W有用=Gh=900 N×5 m=4500 J,
滑轮组的机械效率:η=×100%=×100%≈83.3%.
17.(1)提升重物做的有用功:W有用=Gh=1.2×104 N×2 m=2.4×104 J.
(2)由η=×100%可得,拉力做的总功:W总===3×104 J;由图可知,n=3,绳子自由端移动的距离:s=nh=3×2 m=6 m;由W=Fs可得,拉力F===5000 N.
(3)克服动滑轮重力、摩擦力和钢丝绳重力所做的额外功:W额外=W总-W有用=3×104 J-2.4×104 J=6000 J,提升动滑轮做的额外功:W额1=G动h=m动gh=40 kg×10 N/kg×2 m=800 J,克服摩擦力和钢丝绳重力所做的额外功:W额2=W额外-W额1=6000 J-800 J=5200 J.
18.A 由图知作用在动滑轮上的绳子有2段,则绳端移动的距离为2h,
有用功为W有用=Gh=m2gh,
总功为W总=Fs=F·2h=2Fh,
机械效率为η=×100%=×100%=×100%;
额外功为W额外=W总-W有用=2Fh-m2 gh=(2F-m2g)h,
对吊篮做的功为W1=G1h=m1gh,
对动滑轮做的功为W动=W额外-W1=(2F-m2g)h-m1gh=(2F-m2g-m1g)h;
动滑轮的重力为G动===2F-(m1+m2)g.
同课章节目录
- 第十一章 简单机械和功
- 1 杠杆
- 2 滑轮
- 3 功
- 4 功率
- 5 机械效率
- 第十二章 机械能和内能
- 1 动能 势能 机械能
- 2 内能 热传递
- 3 物质的比热容
- 4 机械能和内能的相互转化
- 第十三章 电路初探
- 1 初识家用电器和电路
- 2 电路连接的基本方式
- 3 电流和电流表的使用
- 4 电压和电压表的使用
- 第十四章 欧姆定律
- 1 电阻
- 2 变阻器
- 3 欧姆定律
- 4 欧姆定律的应用
- 第十五章 电功和电热
- 电能表与电功
- 电功率
- 电热器 电流的热效应
- 家庭电路与安全用电
- 第十六章 电磁转换
- 磁体与磁场
- 电流的磁场
- 磁场对电流的作用 电动机
- 安装直流电动机模型
- 电磁感应 发电机
- 第十七章 电磁波与现代通信
- 信息与信息传播
- 电磁波及其传播
- 现代通信 走进信息时代
- 第十八章 能源与可持续发展
- 能源利用与社会发展
- 核能
- 太阳能
- 能量转化的基本规律
- 能源与可持续发展
