18.1一元二次方程(第1课时)
图片预览






文档简介
课件17张PPT。18.1一元二次方程授课人:李贤武第一课时你还认识“老朋友”吗?1、你还记得什么叫方程?什么叫方程的解吗?
2、什么是一元一次方程?它的一般形式是怎样的?
一般形式:ax+b=0 (a≠0)
3、我们知道了利用一元一次方程可以解决生活中的一些实际问题,你还记得利用一元一次方程解决实际问题的步骤吗?
◆1.审;2.设;3.列;4.解;5.验;6.答。回顾与复习问题情境1 问题1:某地为增加农民收入,需要调整农作物种植结构,计划2007年无公害蔬菜的产量比2005年翻一翻,要实现这一目标,2006年和2007年无公害蔬菜产量的年平均增长率应是多少?
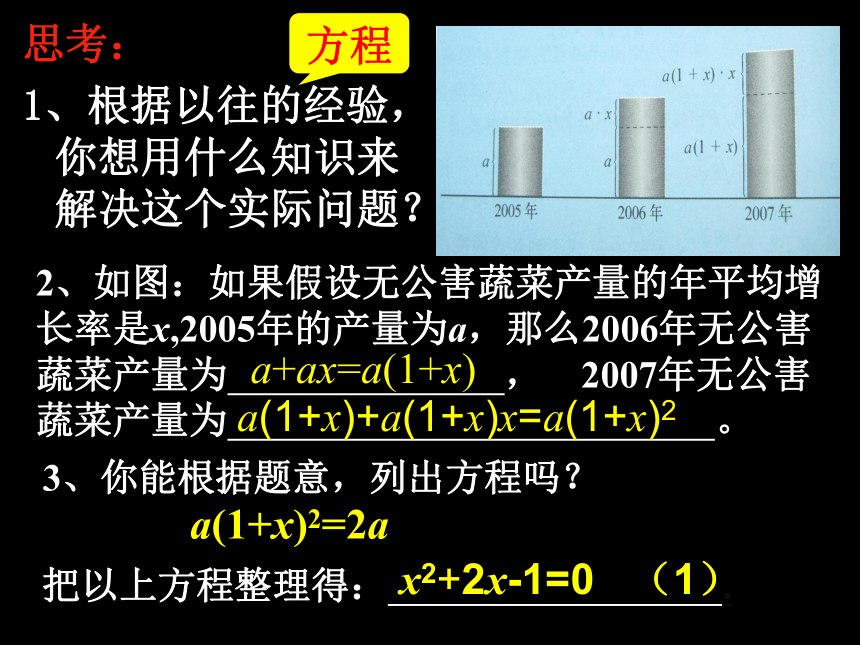
思考:
1、根据以往的经验,你想用什么知识来解决这个实际问题?2、如图:如果假设无公害蔬菜产量的年平均增长率是x,2005年的产量为a,那么2006年无公害蔬菜产量为 ,2007年无公害蔬菜产量为 。 a+ax=a(1+x)a(1+x)+a(1+x)x=a(1+x)23、你能根据题意,列出方程吗?a(1+x)2=2a把以上方程整理得: .x2+2x-1=0 (1)方程
问题2: 在一块宽20m、长32m的矩形空地上,修筑宽相等的三条小路(两条纵向,一条横向,纵向与横向垂直),把矩形空地分成大小一样的六块,建成小花坛。如图要使花坛的总面积为570 m2 ,问小路的宽应为多少?问题情境2 1、若设小路的宽是xm,那么横向小路的面______m2,纵向小路的面积是 m2,两者重叠的面积是 m2. 由于花坛的总面积是 570 m2 ,32x2、你能根据题意,列出方程吗?整理以上方程可得:思考:2×20x32×20-(32x+2×20x)+2x2=5702x2x2-36x+35=0 (2)(20-x)(32-2x)=570想一想:还有其它的列法吗?试说明原因。32-2x20-2x类比发现,探索新知:仔细观察,你会发现什么规律?写出你的结论1、请观察下面两个方程并回答问题:
x2+2x-1=0 x2-36x+35=0
(1)它们是一元一次方程吗?
(2)与一元一次方程有何异同?
(3)通过比较你能归纳出这类方程的特点吗? 1、等号两边都是整式
2、只含有一个未知数
3、未知数的最高次数是2
特点: 一般地,任何一个关于x 的一元二次方程都可以化为 的形式,我们把
(a,b,c为常数,a≠0)称为一元二次方程的一般形式。 为什么要限制a≠0,b、c可以为零吗?想一想: a x 2 + b x + c = 0(a ≠ 0)二次项系数一次项系数常数项(4)通过与一元一次方程的对比,你能给这类方程取个合理的名字吗? ? 例题讲解[例1]判断下列方程是否为一元二次方程?
(1)
(2)
(3)
(4) 例题讲解 将方程(3x-2)(x+1)=8x-3 化为一元二次方程的一般形式,并写出二次项系数、一次项系数及常数项。解:去括号,得3x2+3x-2x-2=8x-3移项,合并同类项得3x2-7x+1=0所以得到一元二次方程的一般形式为:3x2-7x+1=0 其中二次项系数为3,一次项系数为-7,常数项为1。(1)列表填空:4x2-3x=0x2-2x-8=0x2-x-6=04-301-2-81-1-62、做一做:(2)下列方程中哪些是一元二次方程,并说明理由?x+2=5x-3x2=42x2-4=(x+2)2(3)方程(2a- 4)x2 -2bx+a=0在什么条件下为一元二次方程?3、议一议: 通过以上习题的练习的情况,你认为在确定一元二次方程的各项系数及常数项的时候,需要注意哪些?(1)在确定一元二次方程的二次项系数、一次项系数和常数项时必须把方程化为一般形式才能进行。(2)二次项系数、一次项系数以及常数项都要连同它前面的符号。(3)二次项系数a ≠ 0归纳小结 反思提高 本节课学习了哪些内容,有什么收获和体会?布置作业 分层落实拓展题:从前有一天,一个醉汉拿着竹竿进屋,横拿竖拿都进不去,横着比门框宽4尺,竖着比门框高2尺,另一个醉汉教他沿着门的两个对角斜着拿竿,这个醉汉一试,不多不少刚好进去了.你知道竹竿有多长吗?请根据这一问题列出方程.基础题:教材P41习题19.1第1、2题
2、什么是一元一次方程?它的一般形式是怎样的?
一般形式:ax+b=0 (a≠0)
3、我们知道了利用一元一次方程可以解决生活中的一些实际问题,你还记得利用一元一次方程解决实际问题的步骤吗?
◆1.审;2.设;3.列;4.解;5.验;6.答。回顾与复习问题情境1 问题1:某地为增加农民收入,需要调整农作物种植结构,计划2007年无公害蔬菜的产量比2005年翻一翻,要实现这一目标,2006年和2007年无公害蔬菜产量的年平均增长率应是多少?
思考:
1、根据以往的经验,你想用什么知识来解决这个实际问题?2、如图:如果假设无公害蔬菜产量的年平均增长率是x,2005年的产量为a,那么2006年无公害蔬菜产量为 ,2007年无公害蔬菜产量为 。 a+ax=a(1+x)a(1+x)+a(1+x)x=a(1+x)23、你能根据题意,列出方程吗?a(1+x)2=2a把以上方程整理得: .x2+2x-1=0 (1)方程
问题2: 在一块宽20m、长32m的矩形空地上,修筑宽相等的三条小路(两条纵向,一条横向,纵向与横向垂直),把矩形空地分成大小一样的六块,建成小花坛。如图要使花坛的总面积为570 m2 ,问小路的宽应为多少?问题情境2 1、若设小路的宽是xm,那么横向小路的面______m2,纵向小路的面积是 m2,两者重叠的面积是 m2. 由于花坛的总面积是 570 m2 ,32x2、你能根据题意,列出方程吗?整理以上方程可得:思考:2×20x32×20-(32x+2×20x)+2x2=5702x2x2-36x+35=0 (2)(20-x)(32-2x)=570想一想:还有其它的列法吗?试说明原因。32-2x20-2x类比发现,探索新知:仔细观察,你会发现什么规律?写出你的结论1、请观察下面两个方程并回答问题:
x2+2x-1=0 x2-36x+35=0
(1)它们是一元一次方程吗?
(2)与一元一次方程有何异同?
(3)通过比较你能归纳出这类方程的特点吗? 1、等号两边都是整式
2、只含有一个未知数
3、未知数的最高次数是2
特点: 一般地,任何一个关于x 的一元二次方程都可以化为 的形式,我们把
(a,b,c为常数,a≠0)称为一元二次方程的一般形式。 为什么要限制a≠0,b、c可以为零吗?想一想: a x 2 + b x + c = 0(a ≠ 0)二次项系数一次项系数常数项(4)通过与一元一次方程的对比,你能给这类方程取个合理的名字吗? ? 例题讲解[例1]判断下列方程是否为一元二次方程?
(1)
(2)
(3)
(4) 例题讲解 将方程(3x-2)(x+1)=8x-3 化为一元二次方程的一般形式,并写出二次项系数、一次项系数及常数项。解:去括号,得3x2+3x-2x-2=8x-3移项,合并同类项得3x2-7x+1=0所以得到一元二次方程的一般形式为:3x2-7x+1=0 其中二次项系数为3,一次项系数为-7,常数项为1。(1)列表填空:4x2-3x=0x2-2x-8=0x2-x-6=04-301-2-81-1-62、做一做:(2)下列方程中哪些是一元二次方程,并说明理由?x+2=5x-3x2=42x2-4=(x+2)2(3)方程(2a- 4)x2 -2bx+a=0在什么条件下为一元二次方程?3、议一议: 通过以上习题的练习的情况,你认为在确定一元二次方程的各项系数及常数项的时候,需要注意哪些?(1)在确定一元二次方程的二次项系数、一次项系数和常数项时必须把方程化为一般形式才能进行。(2)二次项系数、一次项系数以及常数项都要连同它前面的符号。(3)二次项系数a ≠ 0归纳小结 反思提高 本节课学习了哪些内容,有什么收获和体会?布置作业 分层落实拓展题:从前有一天,一个醉汉拿着竹竿进屋,横拿竖拿都进不去,横着比门框宽4尺,竖着比门框高2尺,另一个醉汉教他沿着门的两个对角斜着拿竿,这个醉汉一试,不多不少刚好进去了.你知道竹竿有多长吗?请根据这一问题列出方程.基础题:教材P41习题19.1第1、2题
