人教A版(2019)选择性必修第一册1.2空间向量基本定理 同步练习(Word版含答案)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册1.2空间向量基本定理 同步练习(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 562.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-24 00:00:00 | ||
图片预览



文档简介
1.2空间向量基本定理同步练习
一、单选题
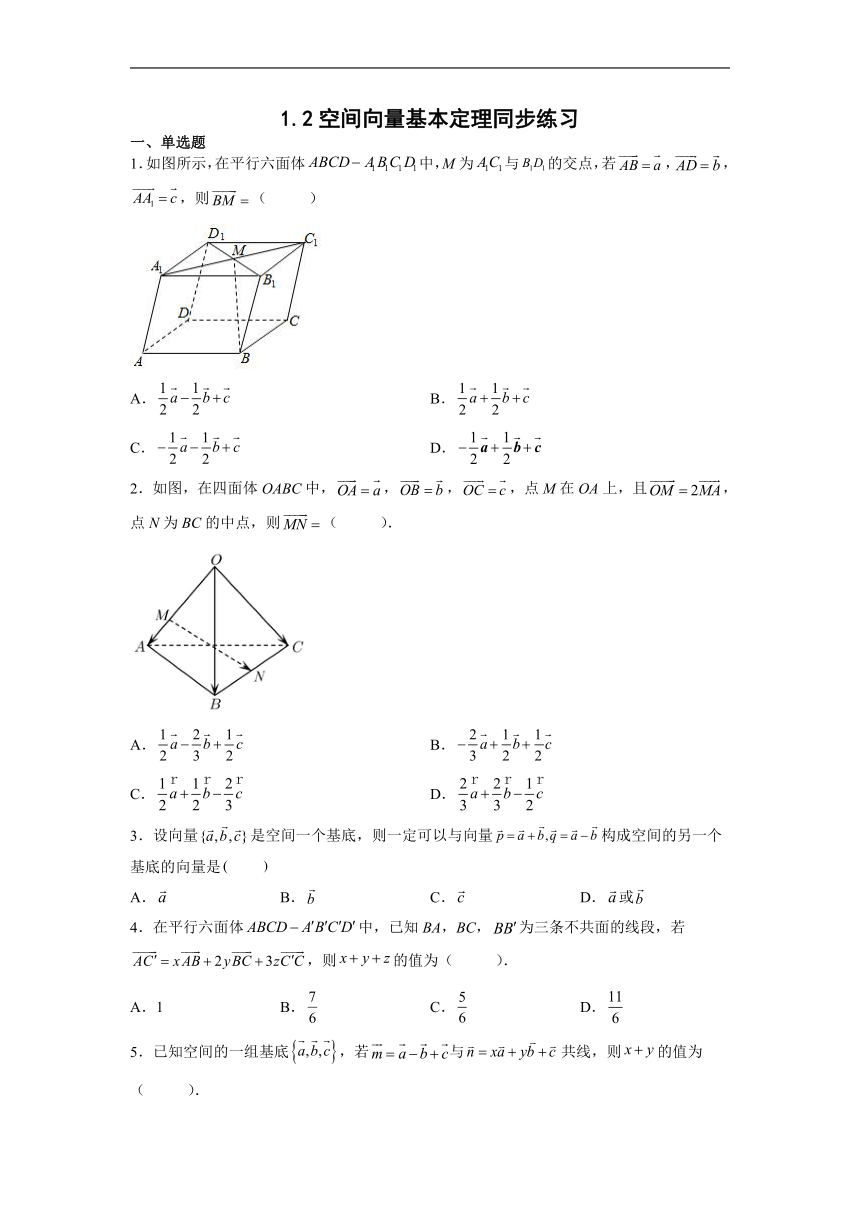
1.如图所示,在平行六面体中,M为与的交点,若,,,则( )
A. B.
C. D.
2.如图,在四面体OABC中,,,,点M在OA上,且,点N为BC的中点,则( ).
A. B.
C. D.
3.设向量是空间一个基底,则一定可以与向量构成空间的另一个基底的向量是
A. B. C. D.或
4.在平行六面体中,已知BA,BC,为三条不共面的线段,若,则的值为( ).
A.1 B. C. D.
5.已知空间的一组基底,若与共线,则的值为( ).
A.2 B. C.1 D.0
6.如图,在平行六面体中,设,,,用基底表示向量,则( )
A. B. C. D.
7.已知,,是不共面的三个向量,下列能构成一组基的是( )
A.,, B.,,
C.,, D.,,
8.设,,,且是空间的一个基底,给出下列向量组:①;②;③;④,则其中可以作为空间的基底的向量组有( )
A.1 B.2 C.3 D.4
二、多选题
9.若构成空间的一个基底,则下列向量共面的是( )
A.,, B.,, C.,, D.,,
10.下列关于空间向量的命题中,正确的有( )
A.若向量,与空间任意向量都不能构成基底,则∥;
B.若非零向量,,满足,,则有∥;
C.若,,是空间的一组基底,且,则,,,四点共面;
D.若,,是空间的一组基底,则向量,,也是空间一组基底;
11.在四面体ABCD中,E是棱BC的中点,且,则下列结论中不正确的是( )
A. B.
C. D.
12.(多选题)已知是不共面的三个向量,则下列向量组中,不能构成一个基底的一组向量是( )
A. B.
C. D.
三、填空题
13.已知是空间五点,且任何三点不共线,若与均不能构成空间的一个基底,则有下列结论:
①不能构成空间的一个基底; ②不能构成空间的一个基底;
③不能构成空间的一个基底; ④能构成空间的一个基底.
其中正确的有_______个.
14.在长方体中,若是棱的中点,是面对角线与的交点,则向量与、___________.(填“共面”或“不共面”)
15.如图,已知在四棱锥中,点E,F分别在棱PB,AD上,且,,以为基底,若,其中x,y,z是实数,则______.
16.已知为半径为的球面上的四点,其中间的球面距离分别为,,,若,其中为球心,则的最大值是__________.
四、解答题
17.如图所示,已知是平行六面体.
(1)化简;
(2)设是底面的中心,是侧面对角线上的分点,设,试求,,的值.
18.如果,那么一定有吗?为什么?
19.如图,在平行六面体中,P是的中点,点Q在上,且,设,,.试用 表示 .
20.如图,已知平行六面体,点G是侧面的中心,且,,.
(1)是否构成空间的一个基底?
(2)如果构成空间的一个基底,那么用它表示下列向量:,,,.
21.在长方体中,是的中点.
(1)设,,,用向量、、表示;
(2)设,,,用向量、、表示
参考答案
题号 1 2 3 4 5 6
答案 D B C B D B
题号 7 8 9 10 11 12
答案 C C ABD ACD ABD ABD
13.3
14.不共面
15.
16.
17.(1)∵是平行六面体,
∴
(2)
∵
,
又,
∴,,.
18.若为非共面向量时,根据向量的基本定理,则一定有;
若为共面向量时,如且时,则,
此时,不一定有;
综上,由不一定有.
19.因为P是的中点,所以.
因为点Q在上,且,所以
.
20.(1),,不在同一平面内,且不为零向量,能构成空间的一个基底;
(2),
,
,
.
21.解:如图,根据向量加法法则得:
.
(2)
解:由(1)得,
因为,
所以,,,
所以,
一、单选题
1.如图所示,在平行六面体中,M为与的交点,若,,,则( )
A. B.
C. D.
2.如图,在四面体OABC中,,,,点M在OA上,且,点N为BC的中点,则( ).
A. B.
C. D.
3.设向量是空间一个基底,则一定可以与向量构成空间的另一个基底的向量是
A. B. C. D.或
4.在平行六面体中,已知BA,BC,为三条不共面的线段,若,则的值为( ).
A.1 B. C. D.
5.已知空间的一组基底,若与共线,则的值为( ).
A.2 B. C.1 D.0
6.如图,在平行六面体中,设,,,用基底表示向量,则( )
A. B. C. D.
7.已知,,是不共面的三个向量,下列能构成一组基的是( )
A.,, B.,,
C.,, D.,,
8.设,,,且是空间的一个基底,给出下列向量组:①;②;③;④,则其中可以作为空间的基底的向量组有( )
A.1 B.2 C.3 D.4
二、多选题
9.若构成空间的一个基底,则下列向量共面的是( )
A.,, B.,, C.,, D.,,
10.下列关于空间向量的命题中,正确的有( )
A.若向量,与空间任意向量都不能构成基底,则∥;
B.若非零向量,,满足,,则有∥;
C.若,,是空间的一组基底,且,则,,,四点共面;
D.若,,是空间的一组基底,则向量,,也是空间一组基底;
11.在四面体ABCD中,E是棱BC的中点,且,则下列结论中不正确的是( )
A. B.
C. D.
12.(多选题)已知是不共面的三个向量,则下列向量组中,不能构成一个基底的一组向量是( )
A. B.
C. D.
三、填空题
13.已知是空间五点,且任何三点不共线,若与均不能构成空间的一个基底,则有下列结论:
①不能构成空间的一个基底; ②不能构成空间的一个基底;
③不能构成空间的一个基底; ④能构成空间的一个基底.
其中正确的有_______个.
14.在长方体中,若是棱的中点,是面对角线与的交点,则向量与、___________.(填“共面”或“不共面”)
15.如图,已知在四棱锥中,点E,F分别在棱PB,AD上,且,,以为基底,若,其中x,y,z是实数,则______.
16.已知为半径为的球面上的四点,其中间的球面距离分别为,,,若,其中为球心,则的最大值是__________.
四、解答题
17.如图所示,已知是平行六面体.
(1)化简;
(2)设是底面的中心,是侧面对角线上的分点,设,试求,,的值.
18.如果,那么一定有吗?为什么?
19.如图,在平行六面体中,P是的中点,点Q在上,且,设,,.试用 表示 .
20.如图,已知平行六面体,点G是侧面的中心,且,,.
(1)是否构成空间的一个基底?
(2)如果构成空间的一个基底,那么用它表示下列向量:,,,.
21.在长方体中,是的中点.
(1)设,,,用向量、、表示;
(2)设,,,用向量、、表示
参考答案
题号 1 2 3 4 5 6
答案 D B C B D B
题号 7 8 9 10 11 12
答案 C C ABD ACD ABD ABD
13.3
14.不共面
15.
16.
17.(1)∵是平行六面体,
∴
(2)
∵
,
又,
∴,,.
18.若为非共面向量时,根据向量的基本定理,则一定有;
若为共面向量时,如且时,则,
此时,不一定有;
综上,由不一定有.
19.因为P是的中点,所以.
因为点Q在上,且,所以
.
20.(1),,不在同一平面内,且不为零向量,能构成空间的一个基底;
(2),
,
,
.
21.解:如图,根据向量加法法则得:
.
(2)
解:由(1)得,
因为,
所以,,,
所以,
