沪教版(五四学制)七年级上册9.9积的乘方课件(共18张PPT)
文档属性
| 名称 | 沪教版(五四学制)七年级上册9.9积的乘方课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 13.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-26 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
9.9 积的乘方
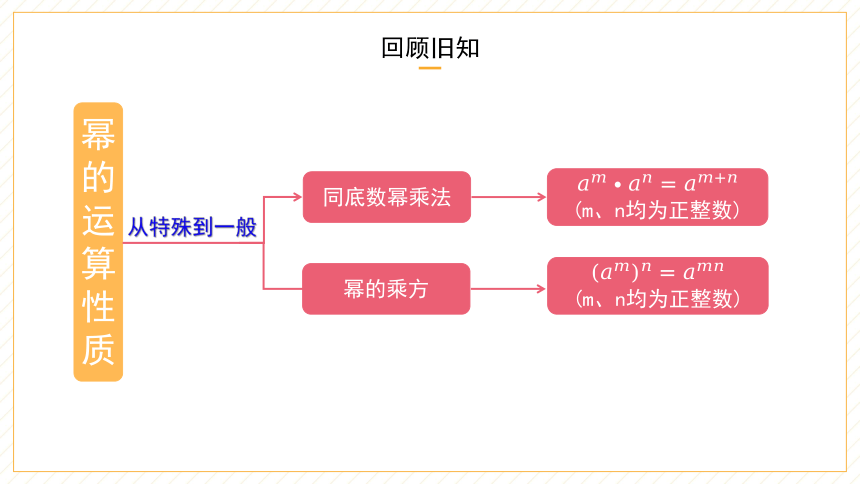
回顾旧知
幂的运算性质
同底数幂乘法
幂的乘方
(m、n均为正整数)
(m、n均为正整数)
从特殊到一般
新课探究
填空并观察
结果和原式有什么联系?
猜想:
验证猜想
(n为正整数)
积的乘方法则:
积的乘方等于把积的每一个因式分别乘方,再把所得的幂相乘.
(n为正整数)
公式推广:
积的乘方
例题讲解
例题讲解
练习:判断
(1) (-a)3· (-a)4 ;
解:原式=(-a)7
=(-1×a)7
=-a7.
是何运算?
例题2 计算:
如何计算(-a)7 ?
如何计算(-a)6 ?
(-a)n= an
(-a)n= -an
-1×a
=(-1)7·a7
当正整数n分别满足什么条件时,
(n为偶数)
(n为奇数)
例题讲解
例题2 计算:
解:原式=3x6y6-2x6y6
=x6y6.
(2) 3(x2y2)3-2(x3y3)2 ;
有哪些运算?
运算顺序如何?
先运用积的乘方法则,
再合并同类项.
积的乘方、整式加减
例题讲解
例题2 计算:
1. 定号
2.进行幂的运算;
3.进行整式加减计算.
运算步骤
(3) 2(x3)2·x3-(3x3)3+(5x)2·x7.
有哪些运算?
运算顺序如何?
积的乘方
同底数幂乘法
整式加减
先乘方、
再乘法、
最后加减
解:原式=2x6·x3-27x9+25x2·x7
=2x9-27x9+25x9
=0.
例题讲解
练习
(3) a3·a4·a+(a2)4+(-2a4)2.
(2) (-2a2)3+9a2·a4;
1. 计算:
(1) (3x3)2+ (2x2)3 ;
例题3 简便运算:
例题讲解
练习
练习
(3) 若x3= -8a6b9,则x=______
(1) 若(a2b3 )n+1 = a6b3m,则m= , n= .
(2) 若(-3x3yn)2 = ax6y8,则a= , n= .
例题4 填空:
例题讲解
课堂练习
课堂练习
课堂练习
课堂小结
幂的运算性质
同底数幂乘法
幂的乘方
(m、n均为正整数)
(m、n均为正整数)
从特殊到一般
积的乘方
(n为正整数)
谢谢观看
9.9 积的乘方
回顾旧知
幂的运算性质
同底数幂乘法
幂的乘方
(m、n均为正整数)
(m、n均为正整数)
从特殊到一般
新课探究
填空并观察
结果和原式有什么联系?
猜想:
验证猜想
(n为正整数)
积的乘方法则:
积的乘方等于把积的每一个因式分别乘方,再把所得的幂相乘.
(n为正整数)
公式推广:
积的乘方
例题讲解
例题讲解
练习:判断
(1) (-a)3· (-a)4 ;
解:原式=(-a)7
=(-1×a)7
=-a7.
是何运算?
例题2 计算:
如何计算(-a)7 ?
如何计算(-a)6 ?
(-a)n= an
(-a)n= -an
-1×a
=(-1)7·a7
当正整数n分别满足什么条件时,
(n为偶数)
(n为奇数)
例题讲解
例题2 计算:
解:原式=3x6y6-2x6y6
=x6y6.
(2) 3(x2y2)3-2(x3y3)2 ;
有哪些运算?
运算顺序如何?
先运用积的乘方法则,
再合并同类项.
积的乘方、整式加减
例题讲解
例题2 计算:
1. 定号
2.进行幂的运算;
3.进行整式加减计算.
运算步骤
(3) 2(x3)2·x3-(3x3)3+(5x)2·x7.
有哪些运算?
运算顺序如何?
积的乘方
同底数幂乘法
整式加减
先乘方、
再乘法、
最后加减
解:原式=2x6·x3-27x9+25x2·x7
=2x9-27x9+25x9
=0.
例题讲解
练习
(3) a3·a4·a+(a2)4+(-2a4)2.
(2) (-2a2)3+9a2·a4;
1. 计算:
(1) (3x3)2+ (2x2)3 ;
例题3 简便运算:
例题讲解
练习
练习
(3) 若x3= -8a6b9,则x=______
(1) 若(a2b3 )n+1 = a6b3m,则m= , n= .
(2) 若(-3x3yn)2 = ax6y8,则a= , n= .
例题4 填空:
例题讲解
课堂练习
课堂练习
课堂练习
课堂小结
幂的运算性质
同底数幂乘法
幂的乘方
(m、n均为正整数)
(m、n均为正整数)
从特殊到一般
积的乘方
(n为正整数)
谢谢观看
