高中数学人教新课标B版必修2--《1.1.6 棱柱、棱锥、棱台和球的表面积》课件(共19张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修2--《1.1.6 棱柱、棱锥、棱台和球的表面积》课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 700.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-24 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
人教B版必修二
教学目标:
1、知识与技能
(1)通过对柱、锥、台体的研究,掌握柱、锥、台的表面积的求法。
(2)能运用公式求解,柱体、锥体、台体和球的表面积。
(3)培养学生空间想象能力和思维能力。
2、过程与方法
(1)让学生经历几何体的侧面展开的过程,感知几何体的形状。
(2)让学生通对照比较,理顺柱体、锥体、台体三间的面积的关系。
3、情感与价值
通过学习,使学生感受到几何体面积的求解过程,对自己空间思维能力影响。从而增强学习的积极性。
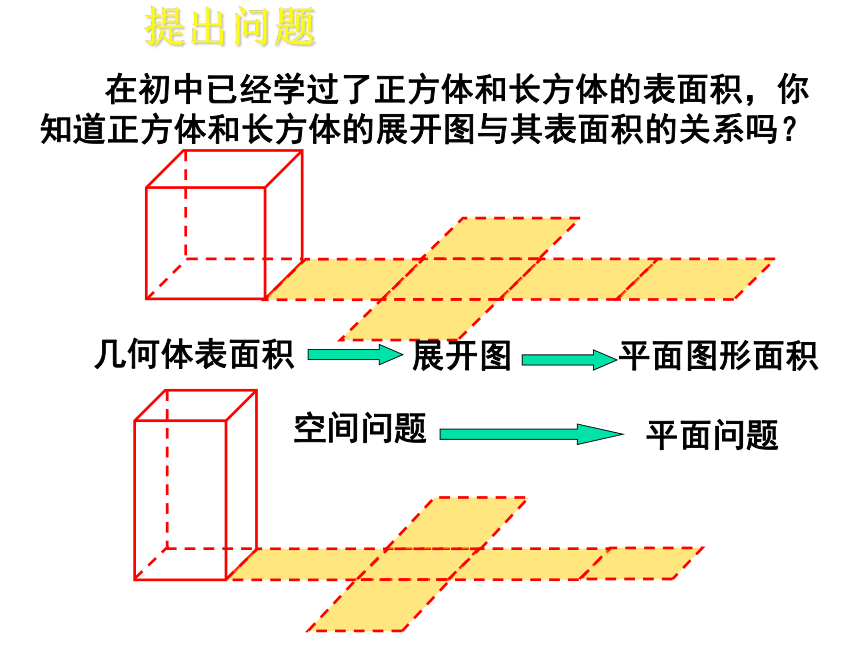
在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?
几何体表面积
展开图
平面图形面积
空间问题
平面问题
提出问题
正方体、长方体是由多个平面围成的几何体,它们的表面积就是各个面的面积的和.
因此,我们可以把它们展成平面图形,利用平面图形求面积的方法,求立体图形的表面积.
引入新课
直棱柱、正棱锥、正棱台都是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?
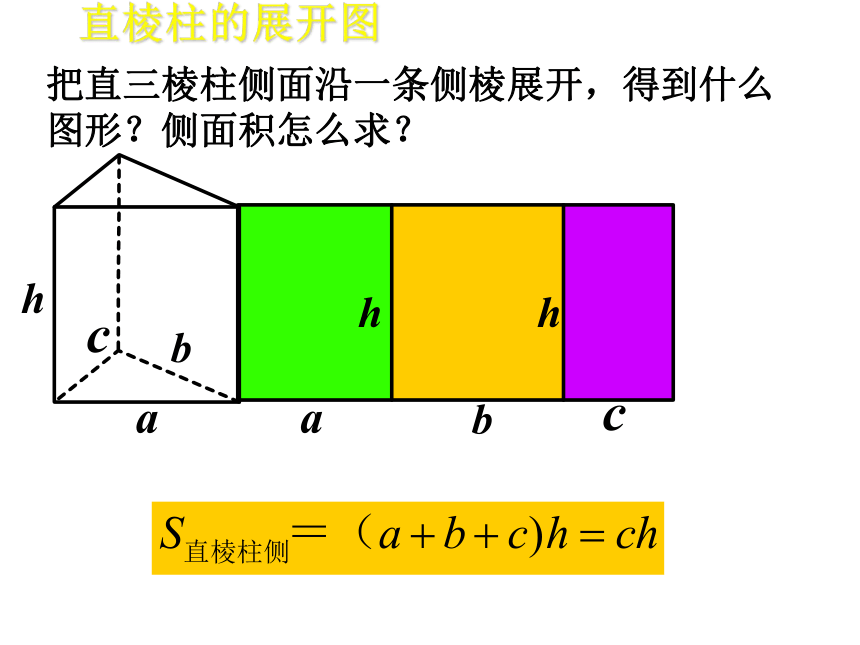
把直三棱柱侧面沿一条侧棱展开,得到什么图形?侧面积怎么求?
直棱柱的展开图
正棱柱的侧面展开图是什么?如何计算它的表面积?
h
正棱柱的展开图
正棱柱的侧面展开图
直棱柱侧
=ch
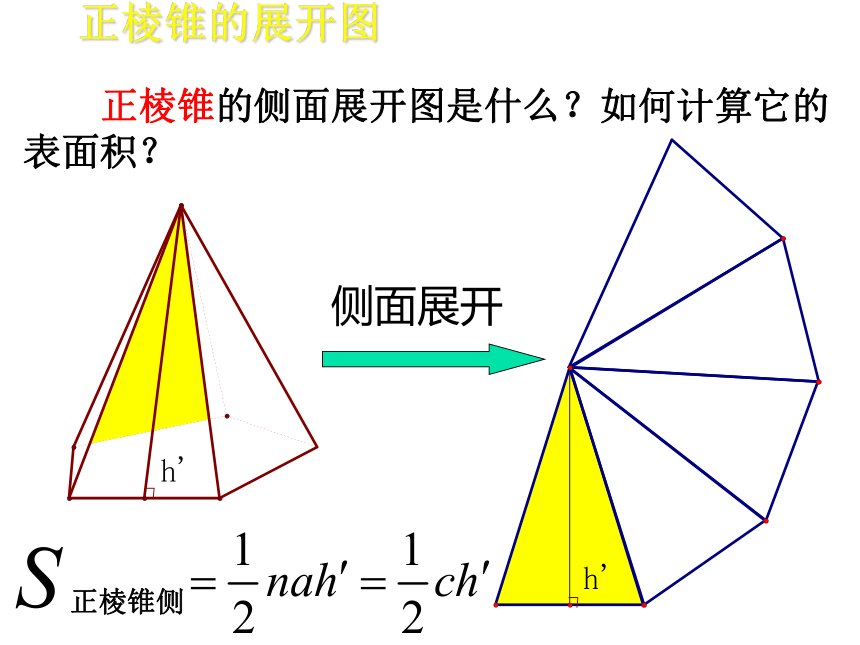
正棱锥的侧面展开图是什么?如何计算它的表面积?
正棱锥的展开图
侧面展开
正棱锥侧
正棱台的侧面展开图是什么?如何计算它的表面积?
正棱台的展开图
侧面展开
h'
h'
正棱台侧
棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧面展开图还是平面图形,计算它们的表面积就是计算它的各个侧面面积和底面面积之和.
h'
表
侧
底
宽=
矩形
把圆柱的侧面沿着一条母线展开,得到什么图形 展开的图形与原图有什么关系?
圆柱的展开图
扇形
把圆锥的侧面沿着一条母线展开,得到什么图形 展开的图形与原图有什么关系?
c
圆锥的展开图
球的表面积:
球面面积(也就是球的表面积)等于它的大圆面积的4倍,即
其中R为球的半径.
球的表面积
已知正六棱台的上、下底面边长分别是2 和4,高是2,则这个棱台的侧面积等于 。
小试牛刀
例1、 已知正四棱锥底面正方形边长为4cm,高与斜高的夹角为30°。
(1)、求正四棱锥的高和斜高的长。
典型例题
(2)、求正四棱锥的侧面积和全面积。
基础过关:
直击高考:
例3.蜜蜂爬行的最短路线问题.
易拉罐的底面直径为8cm,高25cm.
分析: 可以把圆柱沿开始时蜜蜂所在位置的母线展开,
将问题转化为平面几何的问题.
A
B
走进生活:
1、弄清楚柱、锥、台的侧面展开图的形状是关键;
S圆柱=2πrl
S圆锥=πrl
小结:
2、对应的侧面积公式
1、课本 P28.A(1-4)B1
2、探究:P28. B3
课后作业:
人教B版必修二
教学目标:
1、知识与技能
(1)通过对柱、锥、台体的研究,掌握柱、锥、台的表面积的求法。
(2)能运用公式求解,柱体、锥体、台体和球的表面积。
(3)培养学生空间想象能力和思维能力。
2、过程与方法
(1)让学生经历几何体的侧面展开的过程,感知几何体的形状。
(2)让学生通对照比较,理顺柱体、锥体、台体三间的面积的关系。
3、情感与价值
通过学习,使学生感受到几何体面积的求解过程,对自己空间思维能力影响。从而增强学习的积极性。
在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?
几何体表面积
展开图
平面图形面积
空间问题
平面问题
提出问题
正方体、长方体是由多个平面围成的几何体,它们的表面积就是各个面的面积的和.
因此,我们可以把它们展成平面图形,利用平面图形求面积的方法,求立体图形的表面积.
引入新课
直棱柱、正棱锥、正棱台都是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?
把直三棱柱侧面沿一条侧棱展开,得到什么图形?侧面积怎么求?
直棱柱的展开图
正棱柱的侧面展开图是什么?如何计算它的表面积?
h
正棱柱的展开图
正棱柱的侧面展开图
直棱柱侧
=ch
正棱锥的侧面展开图是什么?如何计算它的表面积?
正棱锥的展开图
侧面展开
正棱锥侧
正棱台的侧面展开图是什么?如何计算它的表面积?
正棱台的展开图
侧面展开
h'
h'
正棱台侧
棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧面展开图还是平面图形,计算它们的表面积就是计算它的各个侧面面积和底面面积之和.
h'
表
侧
底
宽=
矩形
把圆柱的侧面沿着一条母线展开,得到什么图形 展开的图形与原图有什么关系?
圆柱的展开图
扇形
把圆锥的侧面沿着一条母线展开,得到什么图形 展开的图形与原图有什么关系?
c
圆锥的展开图
球的表面积:
球面面积(也就是球的表面积)等于它的大圆面积的4倍,即
其中R为球的半径.
球的表面积
已知正六棱台的上、下底面边长分别是2 和4,高是2,则这个棱台的侧面积等于 。
小试牛刀
例1、 已知正四棱锥底面正方形边长为4cm,高与斜高的夹角为30°。
(1)、求正四棱锥的高和斜高的长。
典型例题
(2)、求正四棱锥的侧面积和全面积。
基础过关:
直击高考:
例3.蜜蜂爬行的最短路线问题.
易拉罐的底面直径为8cm,高25cm.
分析: 可以把圆柱沿开始时蜜蜂所在位置的母线展开,
将问题转化为平面几何的问题.
A
B
走进生活:
1、弄清楚柱、锥、台的侧面展开图的形状是关键;
S圆柱=2πrl
S圆锥=πrl
小结:
2、对应的侧面积公式
1、课本 P28.A(1-4)B1
2、探究:P28. B3
课后作业:
