人教新课标A版必修2《2.2.1直线与平面平行的判定》 课件(共18张PPT)
文档属性
| 名称 | 人教新课标A版必修2《2.2.1直线与平面平行的判定》 课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-24 22:11:23 | ||
图片预览





文档简介
(共18张PPT)
2.2.1直线与平面平行的判定
一、复习回顾,引出定理
思考1:
在空间中,直线与平面有哪几种位置关系?
思考2:
是否有更方便、更易于操作的判定线面平行的方法?
二、直观感知,归纳定理
活动1、“直观感知”直线与平面平行的条件
(1)观察开门与关门:
①门扇竖直的两边是什么位置关系?
②当门扇绕着一边转动时,此时门扇转动的一边与门框所在的平面是什么位置关系?
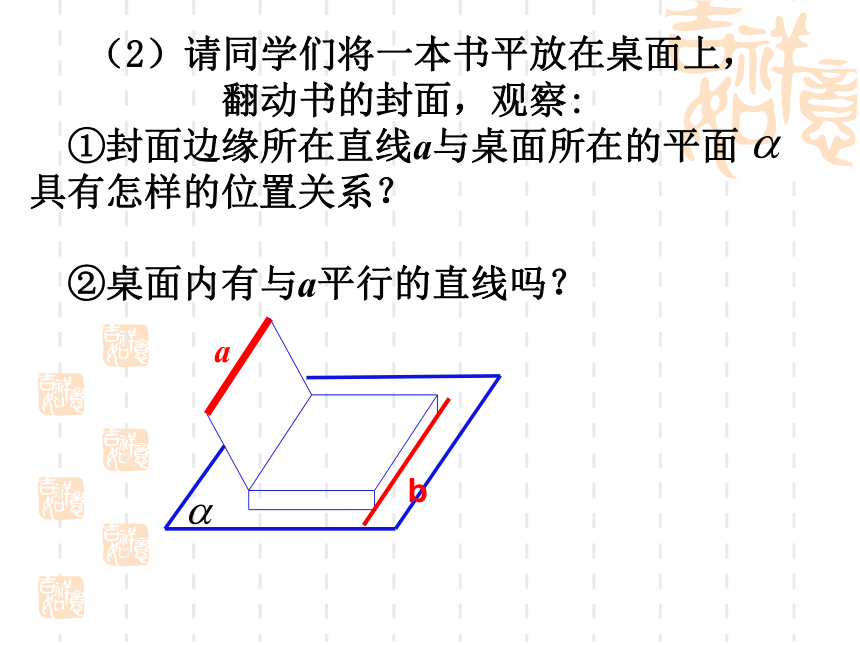
(2)请同学们将一本书平放在桌面上,
翻动书的封面,观察:
①封面边缘所在直线a与桌面所在的平面 具有怎样的位置关系?
②桌面内有与a平行的直线吗?
a
b
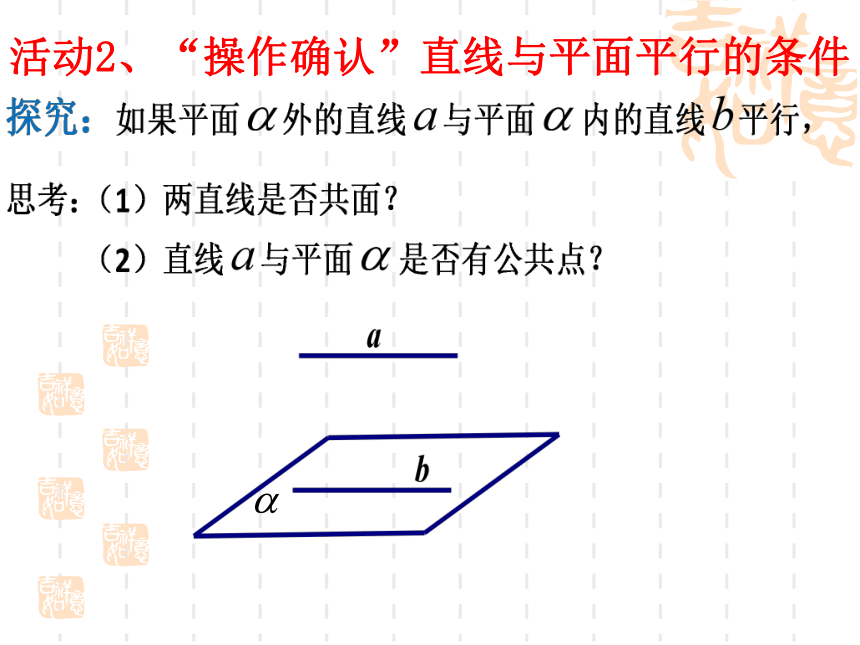
活动2、“操作确认”直线与平面平行的条件
请同学们根据以上直观感知,归纳总结出直线与平面平行的判定定理:
活动3、归纳理解定理
_____________________________________________________________________________________________________________
平面外的一条直线与此平面内的一条直线平行,
则该直线与此平面平行
思考3:判定定理中包含了几个条件?
定理中的关键是什么?
蕴含了什么数学思想?
包含条件:
定理关键:
数学思想:
三、运用定理,尝试练习
求证:空间四边形相邻两边中点的连
平行于经过另外两边所在的平面。
例1
A
B
C
D
E
F
求证:EF∥平面BCD
已知:空间四边形ABCD中,E、F分别是AB、AD的中点.
求证:空间四边形相邻两边中点的连
平行于经过另外两边所在的平面。
例1
A
B
C
D
E
F
如图,在空间四边形ABCD中,E、F分别为AB、AD上的点,若 ,则EF与平面BCD的位置关系是_________.
变式1
变式2
O
思考题
E
四、课堂小结
1.一个定理:
2.一种思想:
3.三种能力:
祝同学们
在充满激情与快乐的学习中
取得丰硕的成果!
【检测与作业】
检测:如图,三棱锥 中, 是侧棱 的中点,现需画一条过点 且与平面 平行的直线,应该怎样完成?
作业:
1、P62习题2.2A组:3.
2、思考题 :在长方体ABCD—A1B1C1D中.
(1)作出过直线AC且与直线 BD1平行的截面,并说明理由.
(2)设E,F分别是A1B和 B1C的中点,求证: 直线EF//平面ABCD.
2.2.1直线与平面平行的判定
一、复习回顾,引出定理
思考1:
在空间中,直线与平面有哪几种位置关系?
思考2:
是否有更方便、更易于操作的判定线面平行的方法?
二、直观感知,归纳定理
活动1、“直观感知”直线与平面平行的条件
(1)观察开门与关门:
①门扇竖直的两边是什么位置关系?
②当门扇绕着一边转动时,此时门扇转动的一边与门框所在的平面是什么位置关系?
(2)请同学们将一本书平放在桌面上,
翻动书的封面,观察:
①封面边缘所在直线a与桌面所在的平面 具有怎样的位置关系?
②桌面内有与a平行的直线吗?
a
b
活动2、“操作确认”直线与平面平行的条件
请同学们根据以上直观感知,归纳总结出直线与平面平行的判定定理:
活动3、归纳理解定理
_____________________________________________________________________________________________________________
平面外的一条直线与此平面内的一条直线平行,
则该直线与此平面平行
思考3:判定定理中包含了几个条件?
定理中的关键是什么?
蕴含了什么数学思想?
包含条件:
定理关键:
数学思想:
三、运用定理,尝试练习
求证:空间四边形相邻两边中点的连
平行于经过另外两边所在的平面。
例1
A
B
C
D
E
F
求证:EF∥平面BCD
已知:空间四边形ABCD中,E、F分别是AB、AD的中点.
求证:空间四边形相邻两边中点的连
平行于经过另外两边所在的平面。
例1
A
B
C
D
E
F
如图,在空间四边形ABCD中,E、F分别为AB、AD上的点,若 ,则EF与平面BCD的位置关系是_________.
变式1
变式2
O
思考题
E
四、课堂小结
1.一个定理:
2.一种思想:
3.三种能力:
祝同学们
在充满激情与快乐的学习中
取得丰硕的成果!
【检测与作业】
检测:如图,三棱锥 中, 是侧棱 的中点,现需画一条过点 且与平面 平行的直线,应该怎样完成?
作业:
1、P62习题2.2A组:3.
2、思考题 :在长方体ABCD—A1B1C1D中.
(1)作出过直线AC且与直线 BD1平行的截面,并说明理由.
(2)设E,F分别是A1B和 B1C的中点,求证: 直线EF//平面ABCD.
