高中数学人教新课标B版必修2--《2.2.1 直线方程的概念与直线的斜率》课件1(共18张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修2--《2.2.1 直线方程的概念与直线的斜率》课件1(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-24 22:11:10 | ||
图片预览



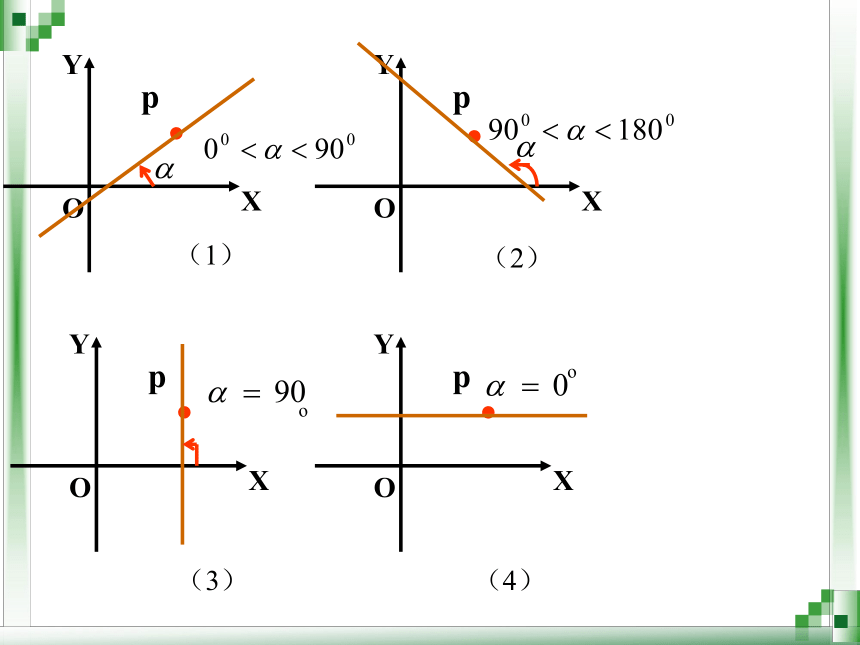


文档简介
(共18张PPT)
圆
直线
直线
圆
3.1.1 直线的倾斜角与斜率
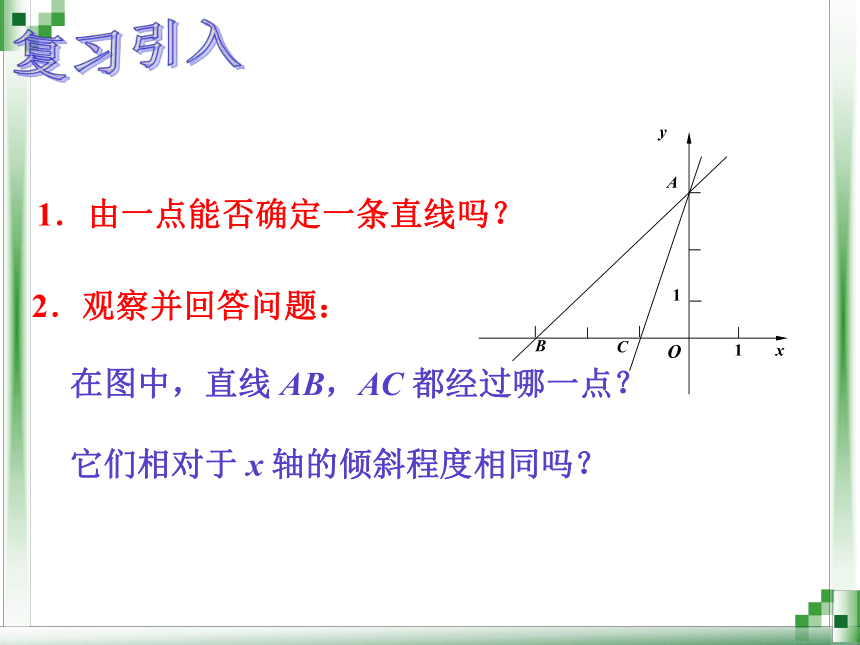
1.由一点能否确定一条直线吗?
2.观察并回答问题:
x
y
B
A
O
1
1
C
在图中,直线 AB,AC 都经过哪一点?
它们相对于 x 轴的倾斜程度相同吗?
一般地,平面直角坐标系内,直线向上
的方向与 x 轴正方向所成的最小正角 叫做
这条直线的倾斜角.
x
y
B
A
O
1
1
直线的倾斜角定义
直线向上的方向
与 x 轴正方向
最小正角
一般地,平面直角坐标系内,直线向上
的方向与 x 轴正向所成的最小正角 叫做这
条直线的倾斜角.
规定:当直线和x轴平行或 重合时,它的倾斜角为0°
直线的倾斜角定义
倾斜角的范围:0 ≤ <180
x
y
B
A
O
1
1
X
.
p
Y
O
X
.
p
Y
O
X
.
p
Y
O
X
.
p
Y
O
(1)
(2)
(4)
(3)
o
o
日常生活中,还有没有表示倾斜程度的量?
前进量
升
高
量
结论:坡度越大,楼梯越陡.
0.8m
1m
0.4m
倾斜角不是 90 的直线,它的倾斜角的正
切值叫做这条直线的斜率,通常用 k 表示,即
直线的斜率定义
k=tan .
练习一
已知直线的倾斜角,求对应的斜率 k :
(1) =0 ; (2) =30 ;
(3) =135 ; (4) =120 .
的定义 =tanα求出直线的斜率;
如果给定直线的倾斜角,我们当然可以根据斜率
如果给定直线上两点坐标,直线是确定的,倾斜
角也是确定的,斜率就是确定的,那么又怎么求出直
线的斜率呢?
已知两点P1(x1,y1)、P2(x2,y2)(其中x1≠x2),
求直线P1P2的斜率
探究:
如图,α为锐角
如图α为钝角,
答:斜率不存在,
因为分母为0。
当直线与坐标轴平行或重合时,上述公式还适用吗?
o
y
x
3.斜率公式
公式的特点:
(1) 与两点的顺序无关;
(2) 公式表明,直线的斜率可以通过直线上任意两
(3) 当x1=x2时,公式不适用,此时α=900
点的坐标来表示,而不需要求出直线的倾斜角
经过两点 的直线的斜率公式
X
.
p
Y
O
X
.
p
Y
O
X
.
p
Y
O
X
.
p
Y
O
(1)
(2)
(4)
(3)
o
o
K>0
K<0
K不存在
K=0
例1:已知点 ,
(1).求直线AB,BC,CA的斜率,并判断这
些直线的倾斜角是锐角还是钝角
O
x
y
A
C
B
(2).过点C的直线 与线段AB有公共点,
求 的斜率k的取值范围
锐角
钝角
锐角
例2、在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2和-3的直线 。
例题分析
O
x
y
A3
A1
A2
A4
(1,1)
(1,-1)
(1,2)
(1,-3)
N(-8,3)
M(2,2)
因为入射角等于反射角
)
0
,
2
(
P
-
\
反射点
(
)
的坐标
求反射点
后过点
轴反射
经过
射出一条光线
从
例3
P
,
)
3
,
8
(
N
x
,
2
,
2
M
-
O
x
y
2
2
-2
P
k=tan ( ≠90 )
1.直线的倾斜角
2.直线的斜率:
(其中x1≠x2)
定义
范围
圆
直线
直线
圆
3.1.1 直线的倾斜角与斜率
1.由一点能否确定一条直线吗?
2.观察并回答问题:
x
y
B
A
O
1
1
C
在图中,直线 AB,AC 都经过哪一点?
它们相对于 x 轴的倾斜程度相同吗?
一般地,平面直角坐标系内,直线向上
的方向与 x 轴正方向所成的最小正角 叫做
这条直线的倾斜角.
x
y
B
A
O
1
1
直线的倾斜角定义
直线向上的方向
与 x 轴正方向
最小正角
一般地,平面直角坐标系内,直线向上
的方向与 x 轴正向所成的最小正角 叫做这
条直线的倾斜角.
规定:当直线和x轴平行或 重合时,它的倾斜角为0°
直线的倾斜角定义
倾斜角的范围:0 ≤ <180
x
y
B
A
O
1
1
X
.
p
Y
O
X
.
p
Y
O
X
.
p
Y
O
X
.
p
Y
O
(1)
(2)
(4)
(3)
o
o
日常生活中,还有没有表示倾斜程度的量?
前进量
升
高
量
结论:坡度越大,楼梯越陡.
0.8m
1m
0.4m
倾斜角不是 90 的直线,它的倾斜角的正
切值叫做这条直线的斜率,通常用 k 表示,即
直线的斜率定义
k=tan .
练习一
已知直线的倾斜角,求对应的斜率 k :
(1) =0 ; (2) =30 ;
(3) =135 ; (4) =120 .
的定义 =tanα求出直线的斜率;
如果给定直线的倾斜角,我们当然可以根据斜率
如果给定直线上两点坐标,直线是确定的,倾斜
角也是确定的,斜率就是确定的,那么又怎么求出直
线的斜率呢?
已知两点P1(x1,y1)、P2(x2,y2)(其中x1≠x2),
求直线P1P2的斜率
探究:
如图,α为锐角
如图α为钝角,
答:斜率不存在,
因为分母为0。
当直线与坐标轴平行或重合时,上述公式还适用吗?
o
y
x
3.斜率公式
公式的特点:
(1) 与两点的顺序无关;
(2) 公式表明,直线的斜率可以通过直线上任意两
(3) 当x1=x2时,公式不适用,此时α=900
点的坐标来表示,而不需要求出直线的倾斜角
经过两点 的直线的斜率公式
X
.
p
Y
O
X
.
p
Y
O
X
.
p
Y
O
X
.
p
Y
O
(1)
(2)
(4)
(3)
o
o
K>0
K<0
K不存在
K=0
例1:已知点 ,
(1).求直线AB,BC,CA的斜率,并判断这
些直线的倾斜角是锐角还是钝角
O
x
y
A
C
B
(2).过点C的直线 与线段AB有公共点,
求 的斜率k的取值范围
锐角
钝角
锐角
例2、在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2和-3的直线 。
例题分析
O
x
y
A3
A1
A2
A4
(1,1)
(1,-1)
(1,2)
(1,-3)
N(-8,3)
M(2,2)
因为入射角等于反射角
)
0
,
2
(
P
-
\
反射点
(
)
的坐标
求反射点
后过点
轴反射
经过
射出一条光线
从
例3
P
,
)
3
,
8
(
N
x
,
2
,
2
M
-
O
x
y
2
2
-2
P
k=tan ( ≠90 )
1.直线的倾斜角
2.直线的斜率:
(其中x1≠x2)
定义
范围
