高中数学人教新课标B版必修2--《2.2.2 直线方程的几种形式》课件1(共19张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修2--《2.2.2 直线方程的几种形式》课件1(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 756.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-24 22:11:52 | ||
图片预览




文档简介
(共19张PPT)
1.理解直线方程的点斜式、斜截式的形式特点和适用范围;
2.能正确利用直线的点斜式、斜截式公式求直线方程;
范围:
1.直线的倾斜角α与斜率k的关系是 __________
3.简述在直角坐标系中确定一条直线的几何要素?
(1)直线上的一点和直线的倾斜角(或斜率)
(2)直线上两点
2.过点 A( , )、B ( , )的直线的斜率
k=_______
直线 l 过点P(2,1),且斜率为3,点Q(x,y)是 l 上不同于P的一点,则x、y满足怎样的关系式?
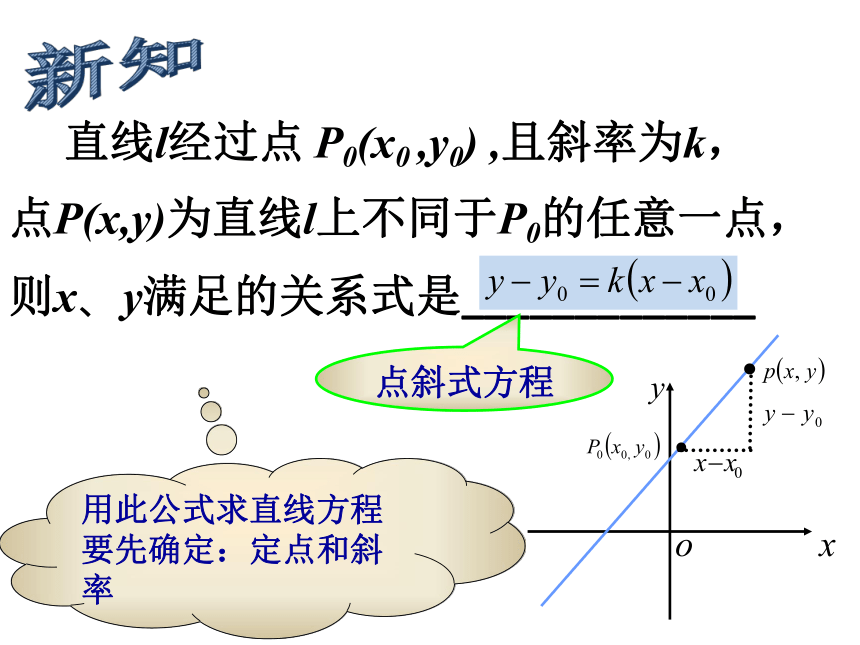
直线l经过点 P0(x0 ,y0) ,且斜率为k,点P(x,y)为直线l上不同于P0的任意一点,则x、y满足的关系式是_____________
用此公式求直线方程要先确定:定点和斜率
点斜式方程
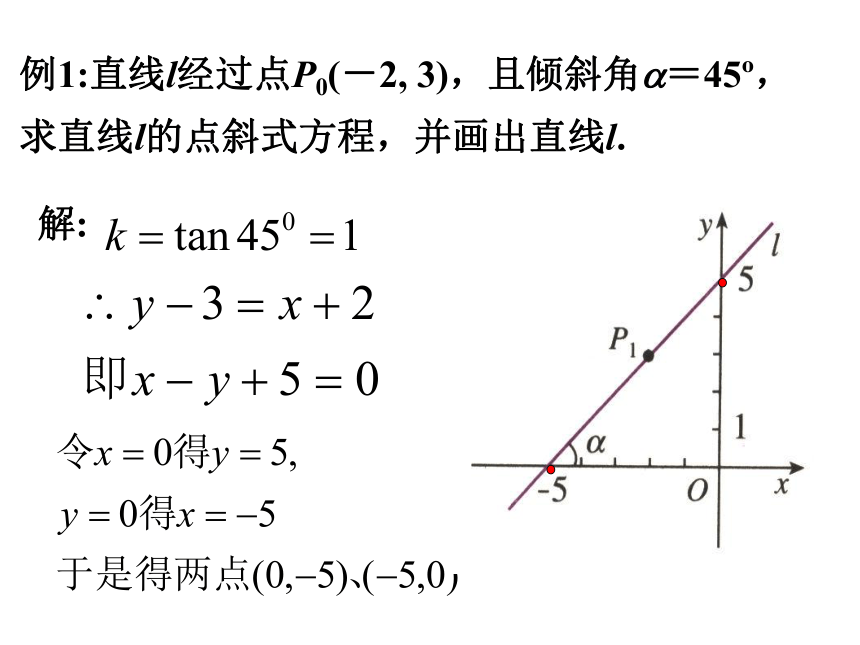
例1:直线l经过点P0(-2, 3),且倾斜角 =45 ,
求直线l的点斜式方程,并画出直线l.
解:
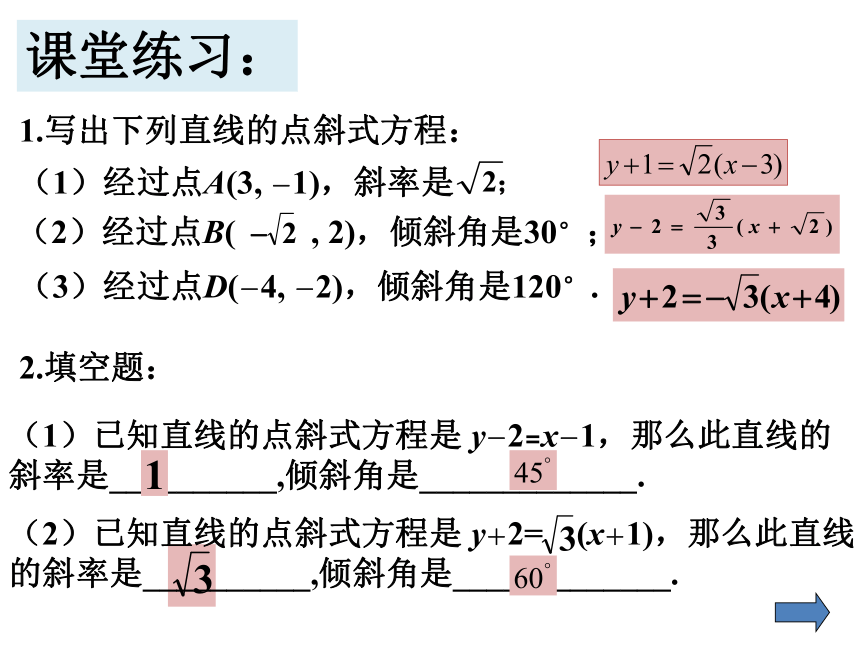
课堂练习:
1.写出下列直线的点斜式方程:
(1)经过点A(3, -1),斜率是
(2)经过点B( , 2),倾斜角是30°;
(3)经过点D(-4, -2),倾斜角是120°.
2.填空题:
(1)已知直线的点斜式方程是 y-2=x-1,那么此直线的
斜率是__________,倾斜角是_____________.
(2)已知直线的点斜式方程是 y+2= (x+1),那么此直线
的斜率是__________,倾斜角是_____________.
经过点 (3,-2),倾斜角为
的直线方程能否用点斜式方程表
示?
例2:求下列直线的方程:
(1)经过点P0(-1, 4),且平行于 轴;
(2)经过点P0(12, -3),且平行于 轴。
思考1:过点 P0(x0 ,y0) ,且与y轴平行的直线,
方程是什么?
思考2:过点 P0(x0 ,y0) ,且与 轴平行的直线,方程是什么?
y-y0=0, 或 y=y0
x-x0=0,或x=x0
思考1:过点 P0(x0 ,y0) ,且与y轴平行
的直线,方程是什么?
思考2:过点 P0(x0 ,y0) ,且与 轴平行的直线,方程是什么?
课堂练习:
1.写出下列直线方程:
(1)经过点A(2, -1),垂直 轴;
(2)经过点B( , ),垂直 轴;
(3)经过点C(0, 3),倾斜角是0°;
注意: 轴所在的直线方程是
轴所在的直线方程是
l
y
O
x
P0(0, b)
斜率
y轴的截距
设直线经过点P0(0,b),其斜率为k,求直线方程.
斜截式
说明:(1)当知道斜率和截距时用斜截式.
(2)斜率k要存在,纵截距b∈R.
y=kx+b ——直线方程的斜截式 .
O
y
x
P(0,b)
A(a,0)
纵截距
横截距
b
a
截距与距离不一样,截距可正、可零、可负,而距离不能为负。
解:
例3:直线l的倾斜角 =60 ,且l 在 y 轴上的
截距为3,求直线l的斜截式方程。
而l的斜截式方程为:
写出下列直线的斜截式方程。
(1) 斜率是 ,在y轴上的截距是-2;
(2) 斜率是-2,在y轴上的截距是4;
答案:
答案:
课堂练习:
形式 条件 直线方程 应用范围
点斜式 过点(x0, y0),且斜率为k
斜截式 在y轴上的截距为b,且斜率为k
斜率存在
斜率存在
(1)
(2)
一般
特殊
平行坐标轴的直线
特殊
1. 预习教材第95页~97页 3.2.2
2. 必做题:教材第100页习题A 1、2、5
3. 选做题:
课后作业:
1.理解直线方程的点斜式、斜截式的形式特点和适用范围;
2.能正确利用直线的点斜式、斜截式公式求直线方程;
范围:
1.直线的倾斜角α与斜率k的关系是 __________
3.简述在直角坐标系中确定一条直线的几何要素?
(1)直线上的一点和直线的倾斜角(或斜率)
(2)直线上两点
2.过点 A( , )、B ( , )的直线的斜率
k=_______
直线 l 过点P(2,1),且斜率为3,点Q(x,y)是 l 上不同于P的一点,则x、y满足怎样的关系式?
直线l经过点 P0(x0 ,y0) ,且斜率为k,点P(x,y)为直线l上不同于P0的任意一点,则x、y满足的关系式是_____________
用此公式求直线方程要先确定:定点和斜率
点斜式方程
例1:直线l经过点P0(-2, 3),且倾斜角 =45 ,
求直线l的点斜式方程,并画出直线l.
解:
课堂练习:
1.写出下列直线的点斜式方程:
(1)经过点A(3, -1),斜率是
(2)经过点B( , 2),倾斜角是30°;
(3)经过点D(-4, -2),倾斜角是120°.
2.填空题:
(1)已知直线的点斜式方程是 y-2=x-1,那么此直线的
斜率是__________,倾斜角是_____________.
(2)已知直线的点斜式方程是 y+2= (x+1),那么此直线
的斜率是__________,倾斜角是_____________.
经过点 (3,-2),倾斜角为
的直线方程能否用点斜式方程表
示?
例2:求下列直线的方程:
(1)经过点P0(-1, 4),且平行于 轴;
(2)经过点P0(12, -3),且平行于 轴。
思考1:过点 P0(x0 ,y0) ,且与y轴平行的直线,
方程是什么?
思考2:过点 P0(x0 ,y0) ,且与 轴平行的直线,方程是什么?
y-y0=0, 或 y=y0
x-x0=0,或x=x0
思考1:过点 P0(x0 ,y0) ,且与y轴平行
的直线,方程是什么?
思考2:过点 P0(x0 ,y0) ,且与 轴平行的直线,方程是什么?
课堂练习:
1.写出下列直线方程:
(1)经过点A(2, -1),垂直 轴;
(2)经过点B( , ),垂直 轴;
(3)经过点C(0, 3),倾斜角是0°;
注意: 轴所在的直线方程是
轴所在的直线方程是
l
y
O
x
P0(0, b)
斜率
y轴的截距
设直线经过点P0(0,b),其斜率为k,求直线方程.
斜截式
说明:(1)当知道斜率和截距时用斜截式.
(2)斜率k要存在,纵截距b∈R.
y=kx+b ——直线方程的斜截式 .
O
y
x
P(0,b)
A(a,0)
纵截距
横截距
b
a
截距与距离不一样,截距可正、可零、可负,而距离不能为负。
解:
例3:直线l的倾斜角 =60 ,且l 在 y 轴上的
截距为3,求直线l的斜截式方程。
而l的斜截式方程为:
写出下列直线的斜截式方程。
(1) 斜率是 ,在y轴上的截距是-2;
(2) 斜率是-2,在y轴上的截距是4;
答案:
答案:
课堂练习:
形式 条件 直线方程 应用范围
点斜式 过点(x0, y0),且斜率为k
斜截式 在y轴上的截距为b,且斜率为k
斜率存在
斜率存在
(1)
(2)
一般
特殊
平行坐标轴的直线
特殊
1. 预习教材第95页~97页 3.2.2
2. 必做题:教材第100页习题A 1、2、5
3. 选做题:
课后作业:
