人教新课标A版必修2《4.1.1圆的标准方程》 课件(共19张PPT)
文档属性
| 名称 | 人教新课标A版必修2《4.1.1圆的标准方程》 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-24 22:14:08 | ||
图片预览






文档简介
(共19张PPT)
圆的标准方程
(1)圆的定义:平面内到__________的距离等于__________的点的集合叫做圆,定点称为圆心,定长称为圆的半径.
圆的标准方程
[导入新知]
4.1.1 圆的标准方程
定点
定长
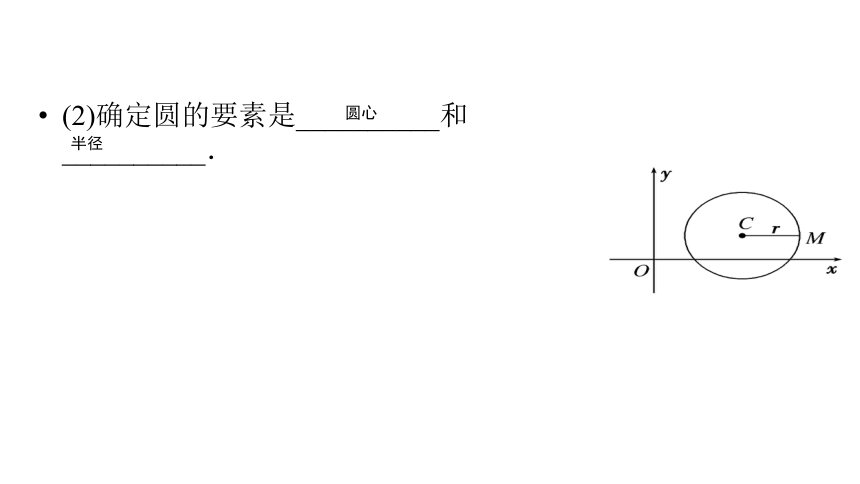
(2)确定圆的要素是__________和__________.
圆心
半径
合作探究
1.圆的标准方程
【问题1】若圆心C坐标为(a,b),试推导圆的标准方程.
【提示】设P点坐标为(x,y),∵ |PC|=r,由两点间距离公式得:
C
P
r
两边平方得:
即为所求圆的方程.
合作探究
2.点与圆的位置关系
【提示】(1)由图可知设A点在圆内,C点在圆上,B点在圆外.
(2)|OA|r.
探究点2
点与圆的位置关系
【问题3】由问题(1)可得出什么结论?
【结论】点与圆的位置关系
设点P到圆心的距离为d,圆的半径为r,则点与圆的位置关系对应如下:
位置关系 点在圆外 点在圆上 点在圆内
d与r的大小关系
d>r
d=r
d<r
典例精讲:题型一:直接法求圆的标准方程
【思路探究】关键是找到圆心与半径,这样就可以写出圆的标准方程.
典例精讲:题型一:直接法求圆的标准方程
【解】:(1)x2+y2=9.
故所求圆的方程为(x-8)2+(y+3)2=25.
(2)(x-3)2+(y-4)2=5.
(3)方法一:
又圆心是点C(8,-3),
∴圆的方程为(x-8)2+(y+3)2=25.
方法二: ∵圆心为C(8,-3),
故设圆的方程为(x-8)2+(y+3)2=r2.
又∵点P(5,1)在圆上,
∴(5-8)2+(1+3)2=r2,
∴r2=25.
典例精讲:题型二:判断点与圆的位置关系
求以点C(3,-5)为圆心,以6为半径的圆的方程,并判断点P1(4,-3),P2(3,1),P3(-3,-4)与这个圆的位置关系.
例2:
分析:(1)根据圆心坐标和半径可得圆的标准方程.
(2)判断点在圆上、圆外、圆内的方法是:根据已知点到圆心的距离与半径的大小关系来判断.
典例精讲:题型二:判断点与圆的位置关系
【解】:(1)圆的方程为(x-3)2+(y+5)2=62.
∴点P3(-3,-4)在圆C外.
∴点P1(4,-3)在圆C内;
∴点P2(3,1)在圆C上;
规律方法
点与圆的位置关系的判断方法:
(1)几何法:将圆心到该点的距离d与圆的半径r比较大小;
(2)代数法:直接利用下面的不等式判定.
①(x0-a)2+(y0-b)2>r2,点(x0,y0)在圆外;
②(x0-a)2+(y0-b)2=r2,点(x0,y0)在圆上;
③(x0-a)2+(y0-b)2拓展提升:待定系数法或几何法求圆的标准方程
求经过A(1,-1),B(-1,1)两点,且圆心在直线x+y-2=0上的圆的方程.
例3:
【思路探究】 思路一:设圆的标准方程(x-a)2+(y-b)2=r2,利用A,B及圆心所在位置求参数a,b,r.
思路二:设圆的圆心坐标C(a,2-a),利用|AC|=|BC|求a及圆的半径.
思路三:利用圆的几何性质:弦AB的中垂线与直线x+y-2=0的交点必为圆心,求圆的标准方程.
拓展提升:待定系数法或几何法求圆的标准方程
因此所求圆的方程为
解法1:
设所求方程为(x-a)2+(y-b)2=r2,
(x-1)2+(y-1)2=4.
x
y
O
x+y-2=0
A(1,-1)
B(-1,1)
C
拓展提升:待定系数法或几何法求圆的标准方程
解法2:
x
y
O
x+y-2=0
A(1,-1)
B(-1,1)
C
故所求圆的标准方程为(x-1)2+(y-1)2=4.
设点C为圆心,
∵点C在直线x+y-2=0上,
∴可设点C的坐标为(a,2-a).
又∵该圆经过A,B两点,
∴|CA|=|CB|.
解得a=1.
∴圆心坐标为C(1,1),
半径长r=|CA|=2.
拓展提升:待定系数法或几何法求圆的标准方程
因此所求圆的方程为
解法3:
由A(1,-1),B(-1,1)可知AB中点为O,
(x-1)2+(y-1)2=4.
x
y
O
x+y-2=0
A(1,-1)
B(-1,1)
y=x
C
故AB中垂线方程为y=x,
即圆心C坐标为(1,1),
圆心在任一弦的中垂线上;
课堂练习
B
课堂练习
B
课堂练习
3.以两点A(-3,-1)和B(5,5)为直径端点的圆的方程是( )
A.(x-1)2+(y-2)2=10
B.(x-1)2+(y-2)2=100
C.(x-1)2+(y-2)2=5
D.(x-1)2+(y-2)2=25
D
归纳小结
1.确定圆的方程主要方法是待定系数法,即列出关于a,b,r的方程组求a,b,r或直接求出圆心(a,b)和半径r.另依据题意适时的运用圆的几何性质解题可以化繁为简,提高解题效率.
2.讨论点与圆的位置关系可以从代数特征(点的坐标是否满足圆的方程)或几何特征(点到圆心的距离与半径的关系)去考虑,其中利用几何特征较为直观、简捷.
圆的标准方程
(1)圆的定义:平面内到__________的距离等于__________的点的集合叫做圆,定点称为圆心,定长称为圆的半径.
圆的标准方程
[导入新知]
4.1.1 圆的标准方程
定点
定长
(2)确定圆的要素是__________和__________.
圆心
半径
合作探究
1.圆的标准方程
【问题1】若圆心C坐标为(a,b),试推导圆的标准方程.
【提示】设P点坐标为(x,y),∵ |PC|=r,由两点间距离公式得:
C
P
r
两边平方得:
即为所求圆的方程.
合作探究
2.点与圆的位置关系
【提示】(1)由图可知设A点在圆内,C点在圆上,B点在圆外.
(2)|OA|
探究点2
点与圆的位置关系
【问题3】由问题(1)可得出什么结论?
【结论】点与圆的位置关系
设点P到圆心的距离为d,圆的半径为r,则点与圆的位置关系对应如下:
位置关系 点在圆外 点在圆上 点在圆内
d与r的大小关系
d>r
d=r
d<r
典例精讲:题型一:直接法求圆的标准方程
【思路探究】关键是找到圆心与半径,这样就可以写出圆的标准方程.
典例精讲:题型一:直接法求圆的标准方程
【解】:(1)x2+y2=9.
故所求圆的方程为(x-8)2+(y+3)2=25.
(2)(x-3)2+(y-4)2=5.
(3)方法一:
又圆心是点C(8,-3),
∴圆的方程为(x-8)2+(y+3)2=25.
方法二: ∵圆心为C(8,-3),
故设圆的方程为(x-8)2+(y+3)2=r2.
又∵点P(5,1)在圆上,
∴(5-8)2+(1+3)2=r2,
∴r2=25.
典例精讲:题型二:判断点与圆的位置关系
求以点C(3,-5)为圆心,以6为半径的圆的方程,并判断点P1(4,-3),P2(3,1),P3(-3,-4)与这个圆的位置关系.
例2:
分析:(1)根据圆心坐标和半径可得圆的标准方程.
(2)判断点在圆上、圆外、圆内的方法是:根据已知点到圆心的距离与半径的大小关系来判断.
典例精讲:题型二:判断点与圆的位置关系
【解】:(1)圆的方程为(x-3)2+(y+5)2=62.
∴点P3(-3,-4)在圆C外.
∴点P1(4,-3)在圆C内;
∴点P2(3,1)在圆C上;
规律方法
点与圆的位置关系的判断方法:
(1)几何法:将圆心到该点的距离d与圆的半径r比较大小;
(2)代数法:直接利用下面的不等式判定.
①(x0-a)2+(y0-b)2>r2,点(x0,y0)在圆外;
②(x0-a)2+(y0-b)2=r2,点(x0,y0)在圆上;
③(x0-a)2+(y0-b)2
求经过A(1,-1),B(-1,1)两点,且圆心在直线x+y-2=0上的圆的方程.
例3:
【思路探究】 思路一:设圆的标准方程(x-a)2+(y-b)2=r2,利用A,B及圆心所在位置求参数a,b,r.
思路二:设圆的圆心坐标C(a,2-a),利用|AC|=|BC|求a及圆的半径.
思路三:利用圆的几何性质:弦AB的中垂线与直线x+y-2=0的交点必为圆心,求圆的标准方程.
拓展提升:待定系数法或几何法求圆的标准方程
因此所求圆的方程为
解法1:
设所求方程为(x-a)2+(y-b)2=r2,
(x-1)2+(y-1)2=4.
x
y
O
x+y-2=0
A(1,-1)
B(-1,1)
C
拓展提升:待定系数法或几何法求圆的标准方程
解法2:
x
y
O
x+y-2=0
A(1,-1)
B(-1,1)
C
故所求圆的标准方程为(x-1)2+(y-1)2=4.
设点C为圆心,
∵点C在直线x+y-2=0上,
∴可设点C的坐标为(a,2-a).
又∵该圆经过A,B两点,
∴|CA|=|CB|.
解得a=1.
∴圆心坐标为C(1,1),
半径长r=|CA|=2.
拓展提升:待定系数法或几何法求圆的标准方程
因此所求圆的方程为
解法3:
由A(1,-1),B(-1,1)可知AB中点为O,
(x-1)2+(y-1)2=4.
x
y
O
x+y-2=0
A(1,-1)
B(-1,1)
y=x
C
故AB中垂线方程为y=x,
即圆心C坐标为(1,1),
圆心在任一弦的中垂线上;
课堂练习
B
课堂练习
B
课堂练习
3.以两点A(-3,-1)和B(5,5)为直径端点的圆的方程是( )
A.(x-1)2+(y-2)2=10
B.(x-1)2+(y-2)2=100
C.(x-1)2+(y-2)2=5
D.(x-1)2+(y-2)2=25
D
归纳小结
1.确定圆的方程主要方法是待定系数法,即列出关于a,b,r的方程组求a,b,r或直接求出圆心(a,b)和半径r.另依据题意适时的运用圆的几何性质解题可以化繁为简,提高解题效率.
2.讨论点与圆的位置关系可以从代数特征(点的坐标是否满足圆的方程)或几何特征(点到圆心的距离与半径的关系)去考虑,其中利用几何特征较为直观、简捷.
