高中数学人教新课标B版必修2--《1.1.7 柱、锥、台和球的体积》课件2(共24张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修2--《1.1.7 柱、锥、台和球的体积》课件2(共24张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-24 22:24:05 | ||
图片预览




文档简介
(共24张PPT)
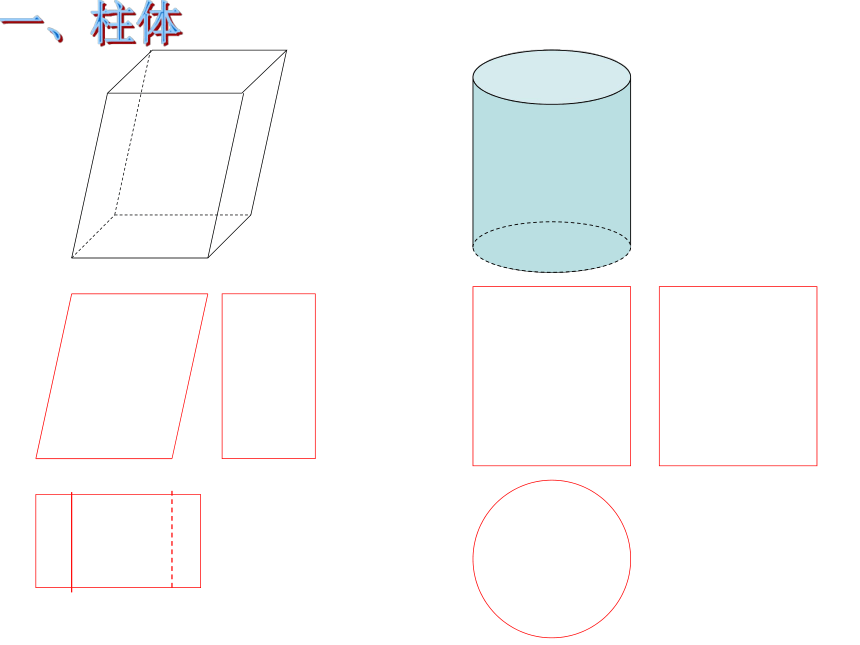
正六棱柱
主
俯
左
棱柱,圆柱
棱锥,圆锥
棱台,圆台
常见几何体:
1.柱体:
2.锥体:
3.台体:
4.球体
柱体三视图特点:
两个平行四边形
棱柱——多边形,几边形就是几棱柱
圆柱——圆
底面
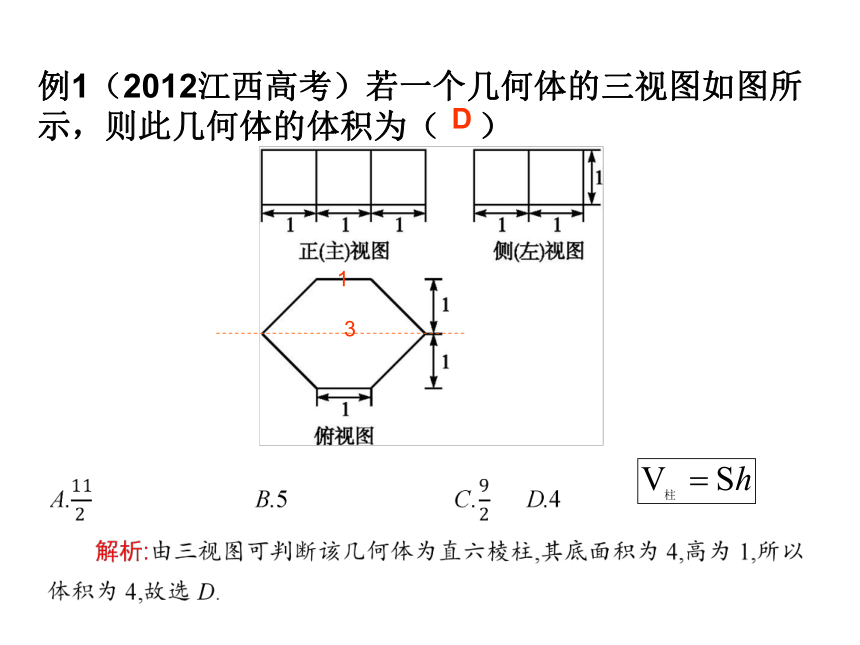
例1(2012江西高考)若一个几何体的三视图如图所示,则此几何体的体积为( )
1
3
D
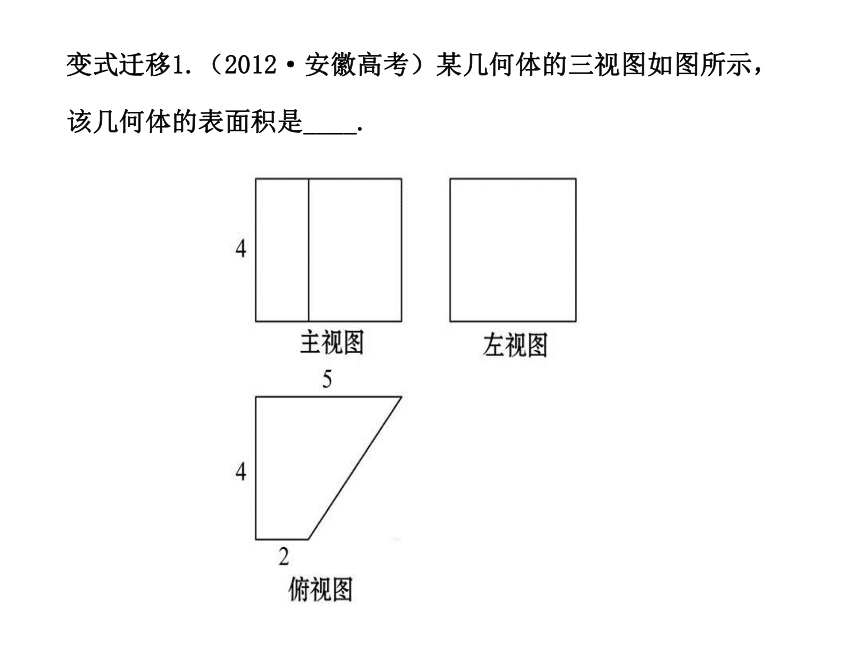
变式迁移1.(2012·安徽高考)某几何体的三视图如图所示,该几何体的表面积是____.
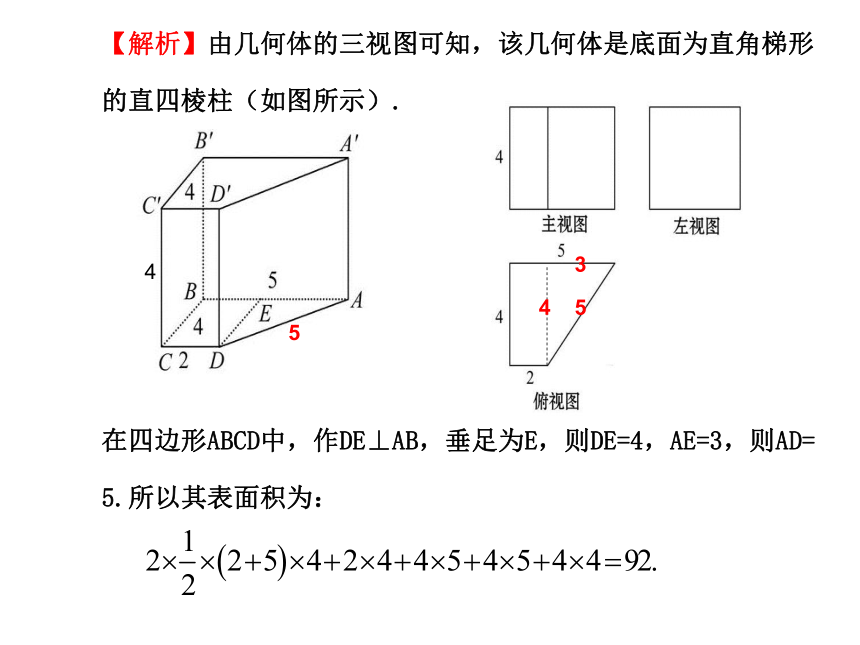
【解析】由几何体的三视图可知,该几何体是底面为直角梯形的直四棱柱(如图所示).
在四边形ABCD中,作DE⊥AB,垂足为E,则DE=4,AE=3,则AD= 5.所以其表面积为:
3
4
5
5
4
主视图
侧视图
俯视图
俯视图
正视图
侧视图
横看成岭侧成峰,远近高低各不同。
不识庐山真面目,只缘身在此山中。
——苏轼
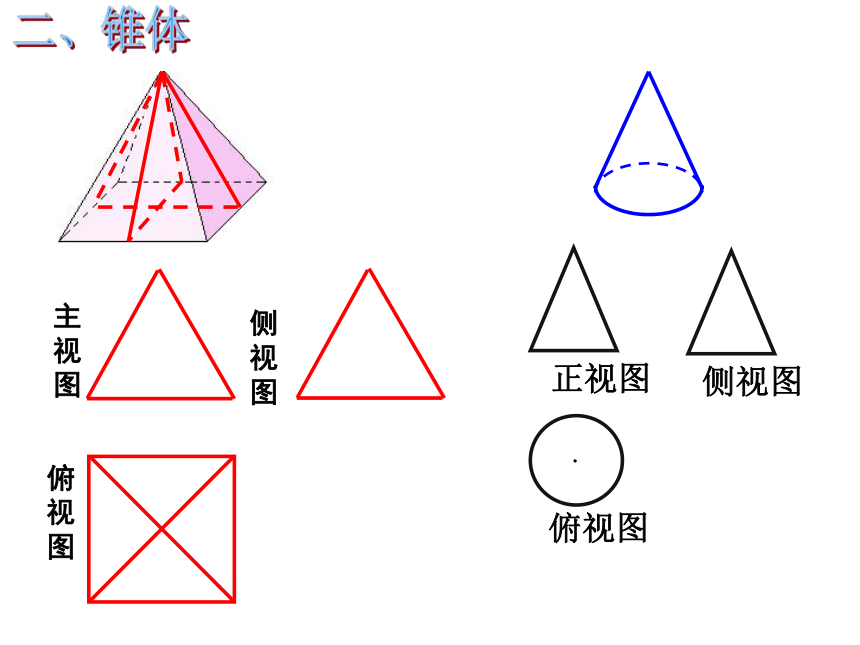
锥体三视图特点:
两个三角形
棱锥——多边形,几边形就是几棱锥
圆锥——圆(通常伴随着圆心)
底面
例2.(2010北京崇文二模)一个几何体的三视图如图所示,则这个几何体的体积等于( )
(A) 12 (B) 4 (C) (D)
V锥=
底
2
2
= ×6×2=4
B
变式迁移2
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )
A、6
B、9
C、12
D、18
该几何体是三棱锥,高为3
此几何体的体积为
B
正视图
侧视图
俯视图
四棱台
主
左
俯
台体三视图特点:
两个梯形
相似但不全等的两个底面
棱台——多边形,几边形就是几棱台。
圆台——同心圆
底面
例3(2010浙江理)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积 是_____
=
=112
=16×2
=32
144
球体三视图特点:都是圆
例4
C
1.(2012·广东高考)某几何体的三视图如图所示,它的体积为( )
(A)12π (B)45π (C)57π (D)81π
【解析】选C.由三视图知该几何体是由圆柱、圆锥两个几何体组合而成,直观图如图所示:
3
4
2.(2015 陕西 5)一个几何体的三视图如图所示,则该几何体的表面积为( )
π· +2π·1× ×2+2×2
D
主
左
俯
3
4
5
6
6
3
4.
5.(2013·北京高考)某四棱锥的三视图如图所示,该四棱锥的体积为 .
【解析】此棱锥底面是边长为3的正方形,高为1,所以体积为
×32×1=3.
3
1.如何还原三视图
柱体三视图特点:两个平行四边形
①棱柱:有两个全等的底面
②圆柱:有圆的出现,矩形。
锥体三视图特点:两个三角形
①棱锥:几棱锥看底面(通常看俯视图),是几边形就是几棱锥。
②圆锥:有圆的出现,通常伴有圆心(圆锥顶点),等腰三角形
台体三视图特点:两个梯形,相似但不全等的两个底面
①棱台:几棱台看底面
②圆台:有同心圆,等腰梯形
球三视图特点:都是圆
2.还原三视图后会求简单的空间几何体体积和表面积等问题。
注意三视图的方向感,利用三视图的长度关系进行计算。
正六棱柱
主
俯
左
棱柱,圆柱
棱锥,圆锥
棱台,圆台
常见几何体:
1.柱体:
2.锥体:
3.台体:
4.球体
柱体三视图特点:
两个平行四边形
棱柱——多边形,几边形就是几棱柱
圆柱——圆
底面
例1(2012江西高考)若一个几何体的三视图如图所示,则此几何体的体积为( )
1
3
D
变式迁移1.(2012·安徽高考)某几何体的三视图如图所示,该几何体的表面积是____.
【解析】由几何体的三视图可知,该几何体是底面为直角梯形的直四棱柱(如图所示).
在四边形ABCD中,作DE⊥AB,垂足为E,则DE=4,AE=3,则AD= 5.所以其表面积为:
3
4
5
5
4
主视图
侧视图
俯视图
俯视图
正视图
侧视图
横看成岭侧成峰,远近高低各不同。
不识庐山真面目,只缘身在此山中。
——苏轼
锥体三视图特点:
两个三角形
棱锥——多边形,几边形就是几棱锥
圆锥——圆(通常伴随着圆心)
底面
例2.(2010北京崇文二模)一个几何体的三视图如图所示,则这个几何体的体积等于( )
(A) 12 (B) 4 (C) (D)
V锥=
底
2
2
= ×6×2=4
B
变式迁移2
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )
A、6
B、9
C、12
D、18
该几何体是三棱锥,高为3
此几何体的体积为
B
正视图
侧视图
俯视图
四棱台
主
左
俯
台体三视图特点:
两个梯形
相似但不全等的两个底面
棱台——多边形,几边形就是几棱台。
圆台——同心圆
底面
例3(2010浙江理)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积 是_____
=
=112
=16×2
=32
144
球体三视图特点:都是圆
例4
C
1.(2012·广东高考)某几何体的三视图如图所示,它的体积为( )
(A)12π (B)45π (C)57π (D)81π
【解析】选C.由三视图知该几何体是由圆柱、圆锥两个几何体组合而成,直观图如图所示:
3
4
2.(2015 陕西 5)一个几何体的三视图如图所示,则该几何体的表面积为( )
π· +2π·1× ×2+2×2
D
主
左
俯
3
4
5
6
6
3
4.
5.(2013·北京高考)某四棱锥的三视图如图所示,该四棱锥的体积为 .
【解析】此棱锥底面是边长为3的正方形,高为1,所以体积为
×32×1=3.
3
1.如何还原三视图
柱体三视图特点:两个平行四边形
①棱柱:有两个全等的底面
②圆柱:有圆的出现,矩形。
锥体三视图特点:两个三角形
①棱锥:几棱锥看底面(通常看俯视图),是几边形就是几棱锥。
②圆锥:有圆的出现,通常伴有圆心(圆锥顶点),等腰三角形
台体三视图特点:两个梯形,相似但不全等的两个底面
①棱台:几棱台看底面
②圆台:有同心圆,等腰梯形
球三视图特点:都是圆
2.还原三视图后会求简单的空间几何体体积和表面积等问题。
注意三视图的方向感,利用三视图的长度关系进行计算。
