高中数学人教新课标B版必修2--《2.2.1 直线方程的概念与直线的斜率》课件2(共21张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修2--《2.2.1 直线方程的概念与直线的斜率》课件2(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 955.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-24 22:24:46 | ||
图片预览

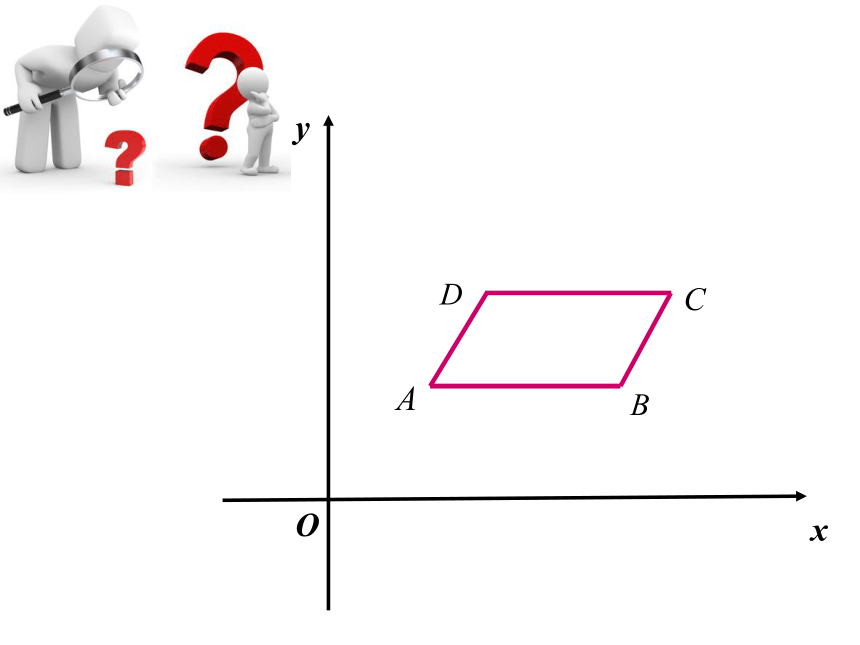

文档简介
(共21张PPT)
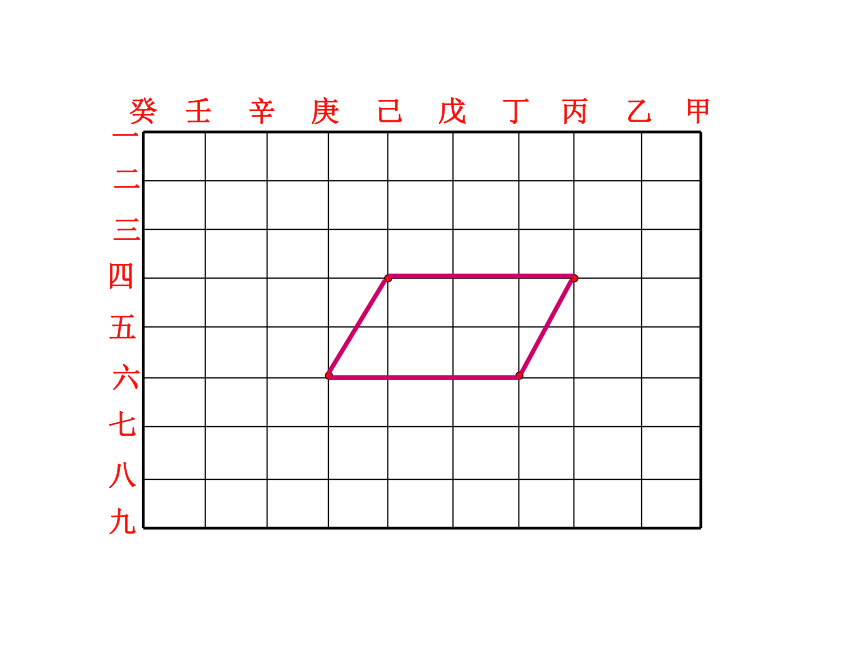
一
二
三
五
四
六
七
八
九
甲
丙
乙
戊
丁
壬
辛
庚
己
癸
y
x
O
对于平面直角坐标系内的一条直线l,确定它的位置的几何要素有哪些?
二、讨论探究
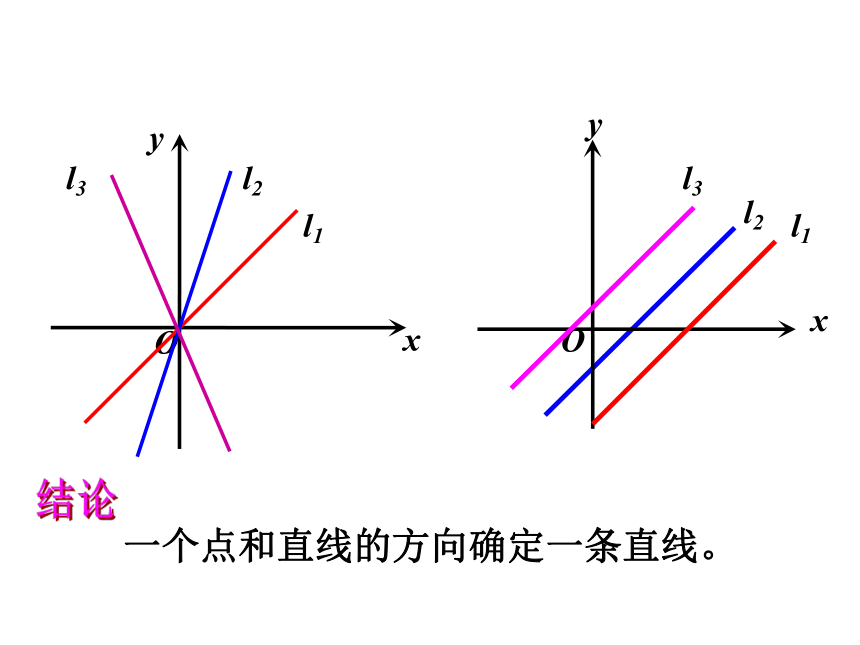
x
y
O
l1
l2
l3
x
y
O
l1
l2
l3
一个点和直线的方向确定一条直线。
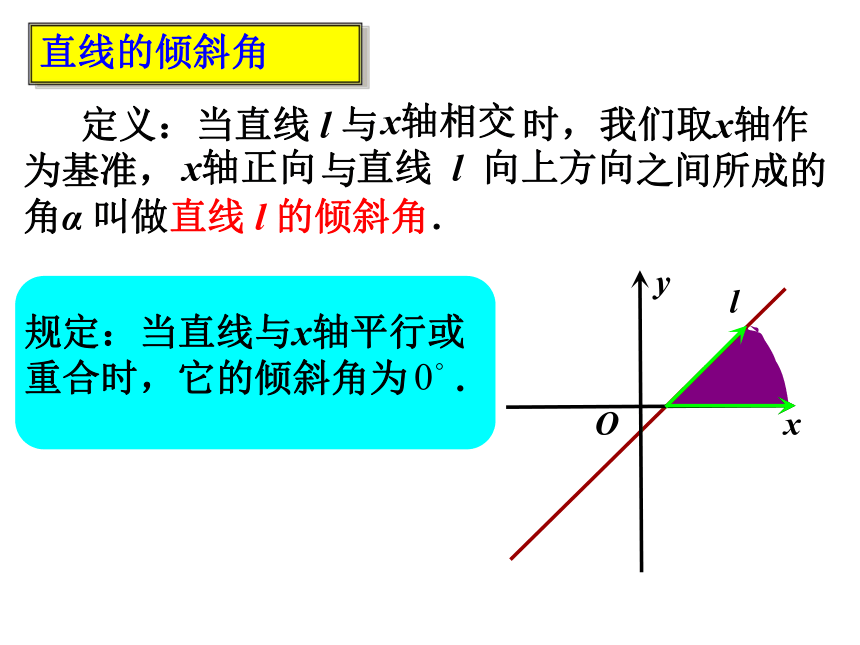
x
y
O
l
定义:当直线 l 与 时,我们取x轴作为基准, 与 之间所成的角α 叫做直线 l 的倾斜角.
直线的倾斜角
规定:当直线与x轴平行或
重合时,它的倾斜角为 .
x轴正向
直线 l 向上方向
x轴相交
O
y
x
l
y
x
l
O
O
y
x
l
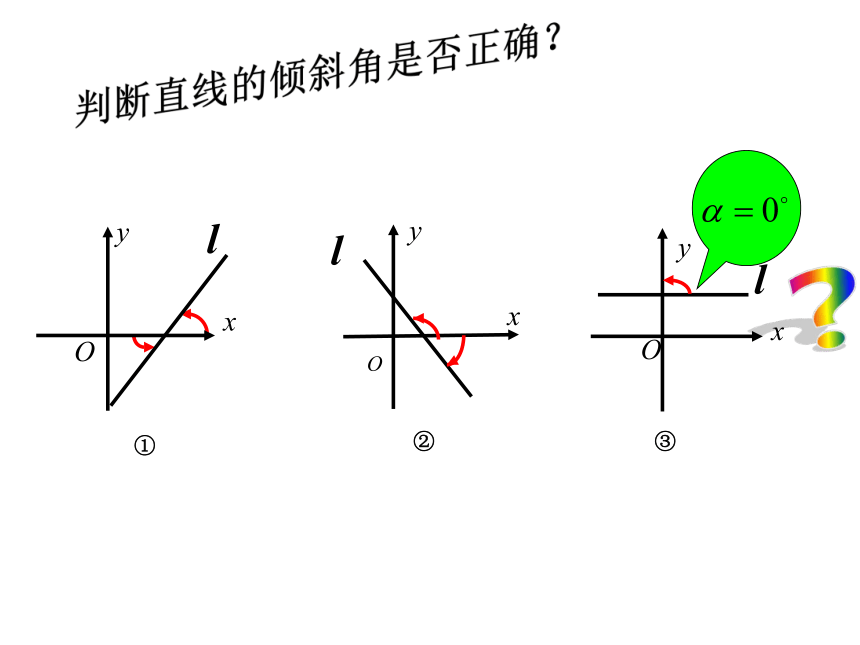
①
②
③
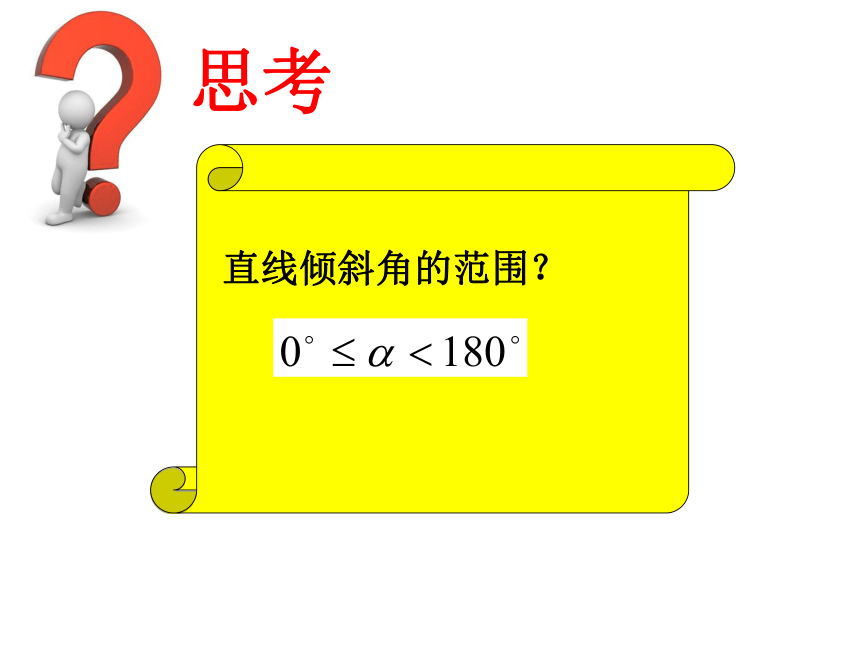
思考
直线倾斜角的范围?
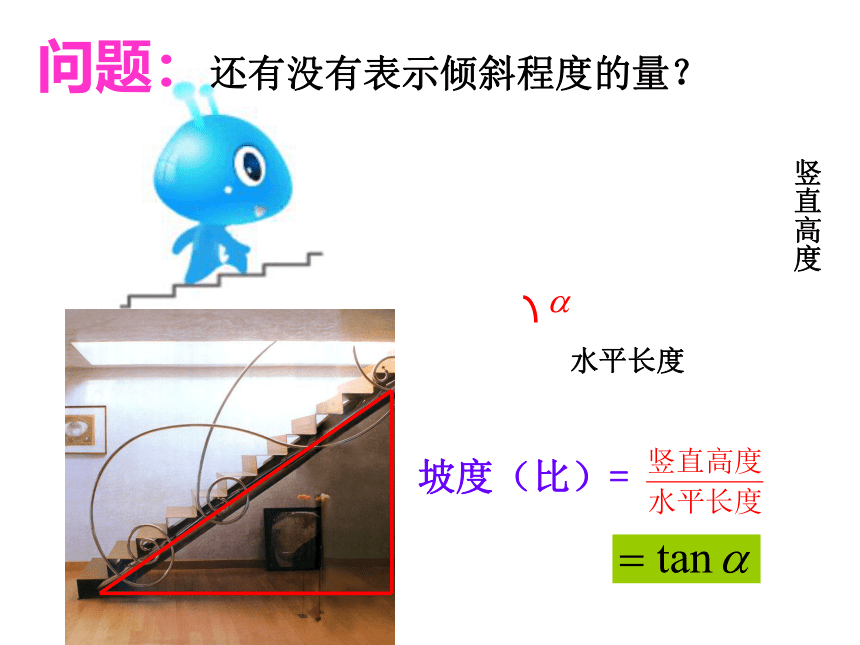
水平长度
竖直高度
问题:还有没有表示倾斜程度的量?
坡度(比)=
直线的斜率
a
tan
=
k
定义:
倾斜角不是 的直线,它的倾斜角的
正切值叫做这条直线的斜率。
斜率通常用 表示,即:
判断正误:
②任一条直线都有倾斜角,所以任一条直线都有
斜率. ( )
③直线的倾斜角越大,则直线的斜率越大. ( )
①平行于x轴的直线的倾斜角是 . ( )
×
×
×
已知直线上两点的坐标,如何计算直线的斜率?
两点的斜率公式
给定两点P1 ( x1 ,y1), P2 ( x2 ,y2)
如何计算直线P1 P2的斜率k.
探究:由两点确定的直线的斜率
如图,当α为锐角时,
锐角
如图,当α为钝角时,
钝角
x
y
o
(3)
y
o
x
(4)
当 的位置对调时, 值又如何呢?
想一想
综上所述,我们得到经过两点
的直线的斜率公式:
当直线平行于x轴或与x轴重合时,此公式仍然适合。
当直线平行于y轴或与y轴重合时,此公式不成立。
两点的斜率公式
1
2
1
2
x
x
y
y
k
-
-
=
例1 如图 ,已知 ,求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
解:直线AB的斜率
直线BC的斜率
直线CA的斜率
由 及 知,直线AB 与CA的倾斜角均为锐角;由 知,直线BC的倾斜角为钝角.
三、应用举例
例2 在平面直角坐标系中,画出经过原点且斜率分别为1,-1及2的直线 及 .
即
解:取 上某一点为 的坐标是 ,根据斜率公式有:
设 ,则 ,于是 的坐标是 .过原点及 的直线即为 .
x
y
是过原点及 的直线, 是过原点及
的直线。
1、直线倾斜角的定义及其范围:
2、直线斜率的定义:
4、斜率公式:
四、课堂小结:知识层面
1
2
1
2
x
x
y
y
k
-
-
=
3、斜率 与倾斜角 之间的关系:
四、课堂小结:思想方法
1.数形结合思想
2.分类讨论思想
五、作业布置
(1) 课本89页习题3.1 A组 1,2,3.
B组 1.
(2) 学案
一
二
三
五
四
六
七
八
九
甲
丙
乙
戊
丁
壬
辛
庚
己
癸
y
x
O
对于平面直角坐标系内的一条直线l,确定它的位置的几何要素有哪些?
二、讨论探究
x
y
O
l1
l2
l3
x
y
O
l1
l2
l3
一个点和直线的方向确定一条直线。
x
y
O
l
定义:当直线 l 与 时,我们取x轴作为基准, 与 之间所成的角α 叫做直线 l 的倾斜角.
直线的倾斜角
规定:当直线与x轴平行或
重合时,它的倾斜角为 .
x轴正向
直线 l 向上方向
x轴相交
O
y
x
l
y
x
l
O
O
y
x
l
①
②
③
思考
直线倾斜角的范围?
水平长度
竖直高度
问题:还有没有表示倾斜程度的量?
坡度(比)=
直线的斜率
a
tan
=
k
定义:
倾斜角不是 的直线,它的倾斜角的
正切值叫做这条直线的斜率。
斜率通常用 表示,即:
判断正误:
②任一条直线都有倾斜角,所以任一条直线都有
斜率. ( )
③直线的倾斜角越大,则直线的斜率越大. ( )
①平行于x轴的直线的倾斜角是 . ( )
×
×
×
已知直线上两点的坐标,如何计算直线的斜率?
两点的斜率公式
给定两点P1 ( x1 ,y1), P2 ( x2 ,y2)
如何计算直线P1 P2的斜率k.
探究:由两点确定的直线的斜率
如图,当α为锐角时,
锐角
如图,当α为钝角时,
钝角
x
y
o
(3)
y
o
x
(4)
当 的位置对调时, 值又如何呢?
想一想
综上所述,我们得到经过两点
的直线的斜率公式:
当直线平行于x轴或与x轴重合时,此公式仍然适合。
当直线平行于y轴或与y轴重合时,此公式不成立。
两点的斜率公式
1
2
1
2
x
x
y
y
k
-
-
=
例1 如图 ,已知 ,求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
解:直线AB的斜率
直线BC的斜率
直线CA的斜率
由 及 知,直线AB 与CA的倾斜角均为锐角;由 知,直线BC的倾斜角为钝角.
三、应用举例
例2 在平面直角坐标系中,画出经过原点且斜率分别为1,-1及2的直线 及 .
即
解:取 上某一点为 的坐标是 ,根据斜率公式有:
设 ,则 ,于是 的坐标是 .过原点及 的直线即为 .
x
y
是过原点及 的直线, 是过原点及
的直线。
1、直线倾斜角的定义及其范围:
2、直线斜率的定义:
4、斜率公式:
四、课堂小结:知识层面
1
2
1
2
x
x
y
y
k
-
-
=
3、斜率 与倾斜角 之间的关系:
四、课堂小结:思想方法
1.数形结合思想
2.分类讨论思想
五、作业布置
(1) 课本89页习题3.1 A组 1,2,3.
B组 1.
(2) 学案
