高中数学人教新课标B版必修2--《2.2.3 两条直线的位置关系》课件2(共25张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修2--《2.2.3 两条直线的位置关系》课件2(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-24 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
a
b
o
平面内如何判断两直线相交?
两直线有公共交点。
平面内如何判断两直线平行?
两直线在同一平面,且无公共交点。
a
b
问题2:在空间中的两条直线呢?
问题1:同一平面内的直线有哪些位置关系?
回顾旧知
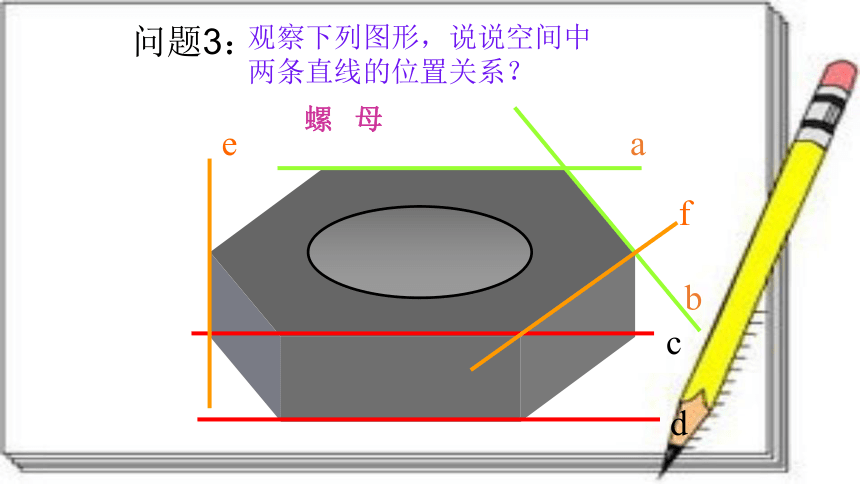
螺 母
a
b
c
d
e
f
问题3:
观察下列图形,说说空间中两条直线的位置关系?
不同在任何一个平面内的两条直线叫 做
异面直线。
问题5:空间两条直线的位置关系有 种?
分别是什么?
共面直线
异面直线
相交直线
平行直线
不同在任何一个平面内,没有公共点。
同一平面内,有且只有一个公共点
同一平面内,没有公共点;
问题4:什么是异面直线?
3
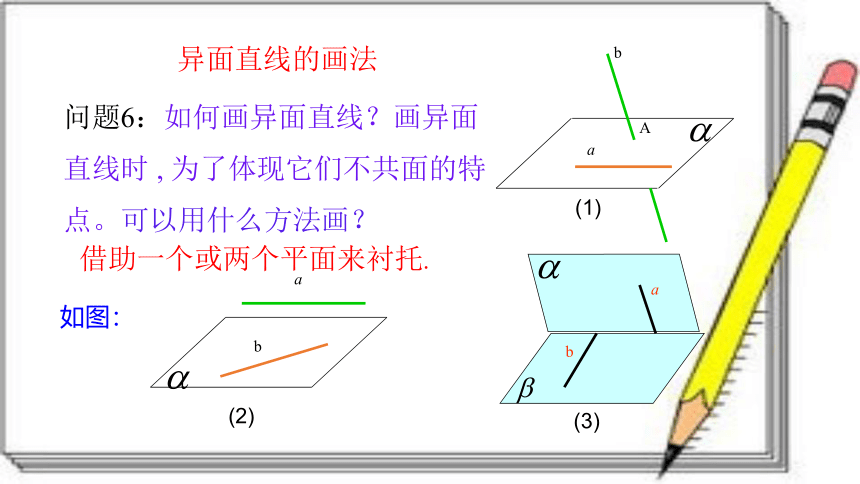
异面直线的画法
问题6:如何画异面直线?画异面直线时 , 为了体现它们不共面的特点。可以用什么方法画?
如图:
a
a
b
a
A
b
b
(1)
(3)
(2)
借助一个或两个平面来衬托.
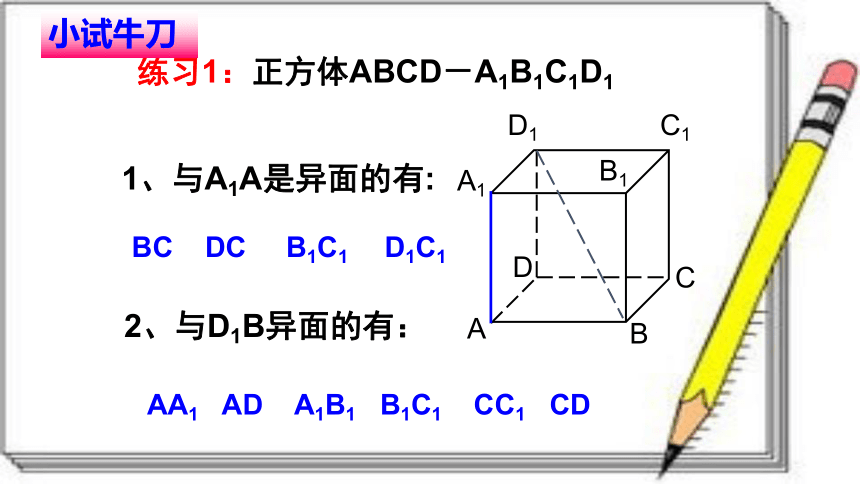
练习1:正方体ABCD-A1B1C1D1
A
B
C
D
A1
B1
C1
D1
1、与A1A是异面的有:
2、与D1B异面的有:
BC DC B1C1 D1C1
AA1 AD A1B1 B1C1 CC1 CD
小试牛刀
练习3:判断下列说法的对错
1、分别在两个平面内的两条直线一定是异面直线;
3、与b是异面直线,b与c是异面直线,则 与c是异面直线;
4、与b共面,b与c共面,则 与c共面
F
F
F
F
巩固提高
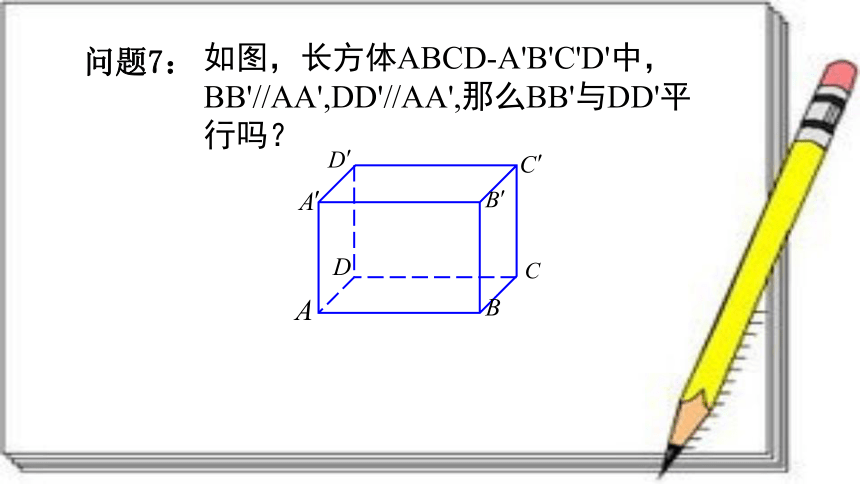
如图,长方体ABCD-A'B'C'D'中,BB'//AA',DD'//AA',那么BB'与DD'平行吗?
问题7:
公理4 平行于同一条直线的两条直线互相平行.
注:
1.直线a,b,c 两两平行,可记为a // b // c .
2.公理4所表述的性质,叫做空间平行线的传递性.
平行公理:
公理4的应用:
A
B
D
E
F
G
H
C
例2:已知ABCD是四个顶点不在同一个平面内的空间四边形,E,F,G,H分别是AB,BC, CD,DA的中点,连结EF,FG,GH,HE,求证:EFGH是一个平行四边形。
证明:连结BD
∵ EH是△ABD的中位线
∴EH ∥BD且EH = BD
同理,FG ∥BD且FG = BD
∴EH ∥FG且EH =FG
∴EFGH是一个平行四边形
变式:如果再加上条件AC = BD,那么四边形EFGH是什么图形?
A
O
B
C
P
D
E
F
Q
问题8:在平面上,如果一个角的两边和另一个 角的两边分别平行,那么这两个角 。
相等或互补
问题9:在空间中这一结论是否仍然成立呢?
如图,四棱柱ABCD--A′B′C′D′ 的底面是平行四边形,∠ADC与∠A′D′C′, ∠ADC与∠B′A′D′的两边分别对应平行,这两组角的大小关系如何
B
A
D
C
A'
B'
D'
C'
B
A
D
C
A'
B'
D'
C'
答:从图中可看出, ∠ADC= ∠A′D′C′,
∠ADC +∠B′A′D′=180
观察
O
等角定理
定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
问题10:这两个角什么时候相等,什么时候互补?
夹角
在平面内两直线相交成四个角,不大于90°的角称为夹角。
a
b
问题11:在平面内可用夹角刻画了一条直线对另一条直线的倾斜程度,异面直线通过 来刻画。
异面直线所成的角
O
O
异面直线所成的角
已知两条异面直线 , b,经过空间任一点O作直线 // , //b,我们把 与 所成的锐角(或直角)叫做异面直线 与b所成的角(或夹角)。
为了简便,O点常取
在某一直线上
平移
若两条异面直线所成角为90°,则称它们互相垂直.
异面直线 与b垂直也记作 ⊥b.
注1:异面直线 、b所成角,只与 、b的相互位置有关, 而与点O位置无关.一般常把点O取在直线 或b上.
注2:异面直线所成角的取值范围:
解:(1)由异面直线的判定方法可知,与直线
成异面直线的有直线
,
A
B
C
D
A'
B'
C'
D'
例3
如图,已知正方体 中。
(1)哪些棱所在直线与直线 是异面直线?
(2)直线 和 的夹角是多少?
(3)哪些棱所在的直线与直线 垂直?
如图,已知正方体 中。
(1)哪些棱所在直线与直线 是异面直线?
(2)直线 和 的夹角是多少?
(3)哪些棱所在的直线与直线 垂直?
解:(2)由 可
知, 等于异面直线 与 的夹角,所以异面直线 与 的夹角为450 。
(3) 直线
与直线 都垂直.
A
B
C
D
A'
B'
C'
D'
例3
1.如图,已知长方体ABCD-EFGH中, AB = , AD = , AE = 2
(1)求BC 和EG 所成的角是多少度
(2)求AE 和BG 所成的角是多少度
解答:
(1)∵GF∥BC
∴∠EGF(或其补角)为所求.
Rt△EFG中,求得∠EGF = 45
o
(2) ∵BF∥AE
∴∠FBG(或其补角)为所求,
Rt△BFG中,求得∠FBG = 60
o
课堂反馈
A
B
G
F
H
E
D
C
2
巩固提高:
解:
作角
证角
算角
答角
不同在 任何 一个平面内的两条直线叫做异面直线.
相交直线
平行直线
异面直线
小结:
在空间平行于同一条直线的两条直线互相平行.
空间中,如果两个角的两边分别对应平行,那么这两个角相等或互补.
辅助平面衬托法
平移,转化为相交直线所成的角
1. 异面直线的定义
2. 空间两直线的位置关系
3. 异面直线的画法
4. 异面直线所成的角
5. 公理4:
6. 等角定理:
7. 计算异面直线所成的角
补充练习
1. 正方体ABCD—A1B1C1D1中,E、F分别为BB1、CC1的中点,求AE、BF所成角的余弦值。
A
D
C
B
A1
D1
C1
B1
2、正方体中若M为A1B1的中点,N为BB1的中点,求异面直线AM与CN所成的角
N
M
F
E
a
b
o
平面内如何判断两直线相交?
两直线有公共交点。
平面内如何判断两直线平行?
两直线在同一平面,且无公共交点。
a
b
问题2:在空间中的两条直线呢?
问题1:同一平面内的直线有哪些位置关系?
回顾旧知
螺 母
a
b
c
d
e
f
问题3:
观察下列图形,说说空间中两条直线的位置关系?
不同在任何一个平面内的两条直线叫 做
异面直线。
问题5:空间两条直线的位置关系有 种?
分别是什么?
共面直线
异面直线
相交直线
平行直线
不同在任何一个平面内,没有公共点。
同一平面内,有且只有一个公共点
同一平面内,没有公共点;
问题4:什么是异面直线?
3
异面直线的画法
问题6:如何画异面直线?画异面直线时 , 为了体现它们不共面的特点。可以用什么方法画?
如图:
a
a
b
a
A
b
b
(1)
(3)
(2)
借助一个或两个平面来衬托.
练习1:正方体ABCD-A1B1C1D1
A
B
C
D
A1
B1
C1
D1
1、与A1A是异面的有:
2、与D1B异面的有:
BC DC B1C1 D1C1
AA1 AD A1B1 B1C1 CC1 CD
小试牛刀
练习3:判断下列说法的对错
1、分别在两个平面内的两条直线一定是异面直线;
3、与b是异面直线,b与c是异面直线,则 与c是异面直线;
4、与b共面,b与c共面,则 与c共面
F
F
F
F
巩固提高
如图,长方体ABCD-A'B'C'D'中,BB'//AA',DD'//AA',那么BB'与DD'平行吗?
问题7:
公理4 平行于同一条直线的两条直线互相平行.
注:
1.直线a,b,c 两两平行,可记为a // b // c .
2.公理4所表述的性质,叫做空间平行线的传递性.
平行公理:
公理4的应用:
A
B
D
E
F
G
H
C
例2:已知ABCD是四个顶点不在同一个平面内的空间四边形,E,F,G,H分别是AB,BC, CD,DA的中点,连结EF,FG,GH,HE,求证:EFGH是一个平行四边形。
证明:连结BD
∵ EH是△ABD的中位线
∴EH ∥BD且EH = BD
同理,FG ∥BD且FG = BD
∴EH ∥FG且EH =FG
∴EFGH是一个平行四边形
变式:如果再加上条件AC = BD,那么四边形EFGH是什么图形?
A
O
B
C
P
D
E
F
Q
问题8:在平面上,如果一个角的两边和另一个 角的两边分别平行,那么这两个角 。
相等或互补
问题9:在空间中这一结论是否仍然成立呢?
如图,四棱柱ABCD--A′B′C′D′ 的底面是平行四边形,∠ADC与∠A′D′C′, ∠ADC与∠B′A′D′的两边分别对应平行,这两组角的大小关系如何
B
A
D
C
A'
B'
D'
C'
B
A
D
C
A'
B'
D'
C'
答:从图中可看出, ∠ADC= ∠A′D′C′,
∠ADC +∠B′A′D′=180
观察
O
等角定理
定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
问题10:这两个角什么时候相等,什么时候互补?
夹角
在平面内两直线相交成四个角,不大于90°的角称为夹角。
a
b
问题11:在平面内可用夹角刻画了一条直线对另一条直线的倾斜程度,异面直线通过 来刻画。
异面直线所成的角
O
O
异面直线所成的角
已知两条异面直线 , b,经过空间任一点O作直线 // , //b,我们把 与 所成的锐角(或直角)叫做异面直线 与b所成的角(或夹角)。
为了简便,O点常取
在某一直线上
平移
若两条异面直线所成角为90°,则称它们互相垂直.
异面直线 与b垂直也记作 ⊥b.
注1:异面直线 、b所成角,只与 、b的相互位置有关, 而与点O位置无关.一般常把点O取在直线 或b上.
注2:异面直线所成角的取值范围:
解:(1)由异面直线的判定方法可知,与直线
成异面直线的有直线
,
A
B
C
D
A'
B'
C'
D'
例3
如图,已知正方体 中。
(1)哪些棱所在直线与直线 是异面直线?
(2)直线 和 的夹角是多少?
(3)哪些棱所在的直线与直线 垂直?
如图,已知正方体 中。
(1)哪些棱所在直线与直线 是异面直线?
(2)直线 和 的夹角是多少?
(3)哪些棱所在的直线与直线 垂直?
解:(2)由 可
知, 等于异面直线 与 的夹角,所以异面直线 与 的夹角为450 。
(3) 直线
与直线 都垂直.
A
B
C
D
A'
B'
C'
D'
例3
1.如图,已知长方体ABCD-EFGH中, AB = , AD = , AE = 2
(1)求BC 和EG 所成的角是多少度
(2)求AE 和BG 所成的角是多少度
解答:
(1)∵GF∥BC
∴∠EGF(或其补角)为所求.
Rt△EFG中,求得∠EGF = 45
o
(2) ∵BF∥AE
∴∠FBG(或其补角)为所求,
Rt△BFG中,求得∠FBG = 60
o
课堂反馈
A
B
G
F
H
E
D
C
2
巩固提高:
解:
作角
证角
算角
答角
不同在 任何 一个平面内的两条直线叫做异面直线.
相交直线
平行直线
异面直线
小结:
在空间平行于同一条直线的两条直线互相平行.
空间中,如果两个角的两边分别对应平行,那么这两个角相等或互补.
辅助平面衬托法
平移,转化为相交直线所成的角
1. 异面直线的定义
2. 空间两直线的位置关系
3. 异面直线的画法
4. 异面直线所成的角
5. 公理4:
6. 等角定理:
7. 计算异面直线所成的角
补充练习
1. 正方体ABCD—A1B1C1D1中,E、F分别为BB1、CC1的中点,求AE、BF所成角的余弦值。
A
D
C
B
A1
D1
C1
B1
2、正方体中若M为A1B1的中点,N为BB1的中点,求异面直线AM与CN所成的角
N
M
F
E
