人教新课标B版必修2《2.3.3 直线与圆的位置关系》 课件(共20张PPT)
文档属性
| 名称 | 人教新课标B版必修2《2.3.3 直线与圆的位置关系》 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 575.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-24 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
新知导入
问题1:图片中,地平线与太阳的位置关系怎样?
问题2:结合初中平面几何中学过的直线与圆的位置关系,直线与圆有几种位置关系?
问题3:如何判断直线与圆的位置关系?
提示:(1)相离 (2)相切 (3)相交
提示:3种,分别是相交、相切、相离.
提示:可利用圆心到直线的距离d与半径r的关系.
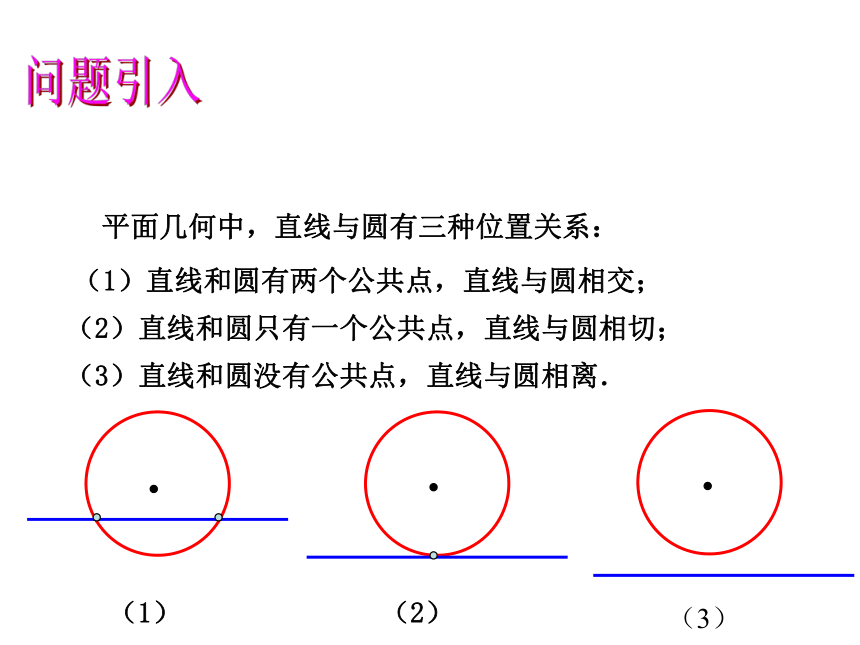
平面几何中,直线与圆有三种位置关系:
(1)直线和圆有两个公共点,直线与圆相交;
(1)
(2)直线和圆只有一个公共点,直线与圆相切;
(2)
(3)直线和圆没有公共点,直线与圆相离.
(3)
C
l
d
r
C
l
C
l
直线与圆的位置关系
利用圆心到直线的距离d与半径r的关系
2、现在,如何用直线方程和圆的方程判断它们之间的位置关系?
先看以下问题,看看你能否从问题中总结出来.
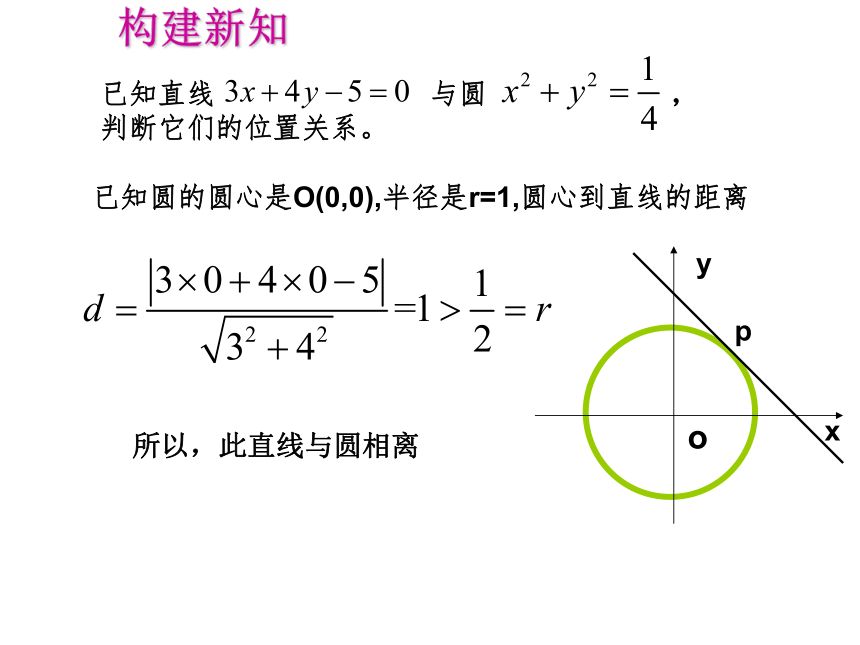
已知直线 与圆 ,
判断它们的位置关系。
已知圆的圆心是O(0,0),半径是r=1,圆心到直线的距离
所以,此直线与圆相离
x
y
o
p
构建新知
已知直线 与圆 ,
判断它们的位置关系。
建立方程组
②
①
由①可知
,代入②中
得
,化简得
则直线与圆相离
构建新知
判断直线与圆的位置关系有两种方法:
代数法:根据直线与圆的方程组成的方程组解的情况来判断.如果有两组实数解时,直线与圆相交;有一组实数解时,直线与圆相切;无实数解时,直线与圆相离.
几何法:根据圆心到直线的距离d与圆的半径r的关系来判断.如果d< r ,直线与圆相交;如果d= r ,直线与圆相切;如果d> r ,直线与圆相离.
回顾我们前面提出的问题:如何用直线和圆的方程判断它们之间的位置关系?
解法一:圆 可化为
其圆心C的坐标为(0,1),半径长为 ,点C (0,1)到直线 l 的距离
所以,直线 l 与圆相交.
分析:依据圆心到直线的距离与半径长的关系,
判断直线与圆的位置关系(几何法);
例1、如图,已知直线l: 和圆心为C的圆 ,判断直线 l 与圆的位置关系;
解法二:
所以,直线与圆有两个交点,直线 l 与圆相交。
分析 :根据直线与圆的方程组成的方程组解的情况来判断(代数法)
例1、如图,已知直线l: 和圆心为C的圆 ,判断直线 l 与圆的位置关系;
①
②
代入②,
由①可得
消去y, 得
变式:设直线 和圆 相切,
求实数m的值。
解法一:已知圆的圆心为O( 0, 0), 半径r =1,
则O到已知直线的距离
由已知得 d=r , 即
解得 m=
O
(0,2)
x
y
变式: 设直线 和圆 相切,
求实数m的值。
O
2
x
y
解法二:把直线方程与圆的方程联立得
把①代入②中得
由直线和圆相切可得:
练习:
1、判断直线
与圆
的位置关系。
2、以C(1,3)为圆心, 为半径的圆与直线
相切,求实数m的值
切 线 问 题
x
y
o
p
切 线 问 题
讨论:
把直线方程代入圆的方程
得到一元 二次方程
求出△的值
确定圆的圆心坐标和半径r
计算圆心到直线的距离d
判断 d与圆半径r的大小关系
归纳小节 直线和圆的位置关系的判断方法
几何方法
代数方法
作业
3.已知⊙C:(x-1)2+(y-2) 2=2,P(2,3),过P作⊙C的切线,
求切线方程 。
新知导入
问题1:图片中,地平线与太阳的位置关系怎样?
问题2:结合初中平面几何中学过的直线与圆的位置关系,直线与圆有几种位置关系?
问题3:如何判断直线与圆的位置关系?
提示:(1)相离 (2)相切 (3)相交
提示:3种,分别是相交、相切、相离.
提示:可利用圆心到直线的距离d与半径r的关系.
平面几何中,直线与圆有三种位置关系:
(1)直线和圆有两个公共点,直线与圆相交;
(1)
(2)直线和圆只有一个公共点,直线与圆相切;
(2)
(3)直线和圆没有公共点,直线与圆相离.
(3)
C
l
d
r
C
l
C
l
直线与圆的位置关系
利用圆心到直线的距离d与半径r的关系
2、现在,如何用直线方程和圆的方程判断它们之间的位置关系?
先看以下问题,看看你能否从问题中总结出来.
已知直线 与圆 ,
判断它们的位置关系。
已知圆的圆心是O(0,0),半径是r=1,圆心到直线的距离
所以,此直线与圆相离
x
y
o
p
构建新知
已知直线 与圆 ,
判断它们的位置关系。
建立方程组
②
①
由①可知
,代入②中
得
,化简得
则直线与圆相离
构建新知
判断直线与圆的位置关系有两种方法:
代数法:根据直线与圆的方程组成的方程组解的情况来判断.如果有两组实数解时,直线与圆相交;有一组实数解时,直线与圆相切;无实数解时,直线与圆相离.
几何法:根据圆心到直线的距离d与圆的半径r的关系来判断.如果d< r ,直线与圆相交;如果d= r ,直线与圆相切;如果d> r ,直线与圆相离.
回顾我们前面提出的问题:如何用直线和圆的方程判断它们之间的位置关系?
解法一:圆 可化为
其圆心C的坐标为(0,1),半径长为 ,点C (0,1)到直线 l 的距离
所以,直线 l 与圆相交.
分析:依据圆心到直线的距离与半径长的关系,
判断直线与圆的位置关系(几何法);
例1、如图,已知直线l: 和圆心为C的圆 ,判断直线 l 与圆的位置关系;
解法二:
所以,直线与圆有两个交点,直线 l 与圆相交。
分析 :根据直线与圆的方程组成的方程组解的情况来判断(代数法)
例1、如图,已知直线l: 和圆心为C的圆 ,判断直线 l 与圆的位置关系;
①
②
代入②,
由①可得
消去y, 得
变式:设直线 和圆 相切,
求实数m的值。
解法一:已知圆的圆心为O( 0, 0), 半径r =1,
则O到已知直线的距离
由已知得 d=r , 即
解得 m=
O
(0,2)
x
y
变式: 设直线 和圆 相切,
求实数m的值。
O
2
x
y
解法二:把直线方程与圆的方程联立得
把①代入②中得
由直线和圆相切可得:
练习:
1、判断直线
与圆
的位置关系。
2、以C(1,3)为圆心, 为半径的圆与直线
相切,求实数m的值
切 线 问 题
x
y
o
p
切 线 问 题
讨论:
把直线方程代入圆的方程
得到一元 二次方程
求出△的值
确定圆的圆心坐标和半径r
计算圆心到直线的距离d
判断 d与圆半径r的大小关系
归纳小节 直线和圆的位置关系的判断方法
几何方法
代数方法
作业
3.已知⊙C:(x-1)2+(y-2) 2=2,P(2,3),过P作⊙C的切线,
求切线方程 。
