人教A版(2019)选择性必修第一册1.2空间向量基本定理 课件(共15张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册1.2空间向量基本定理 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 568.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-24 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
1.2 空间向量基本定理
第一章 空间向量与立体几何
目录
二、知识讲解
三、小结
四、练习
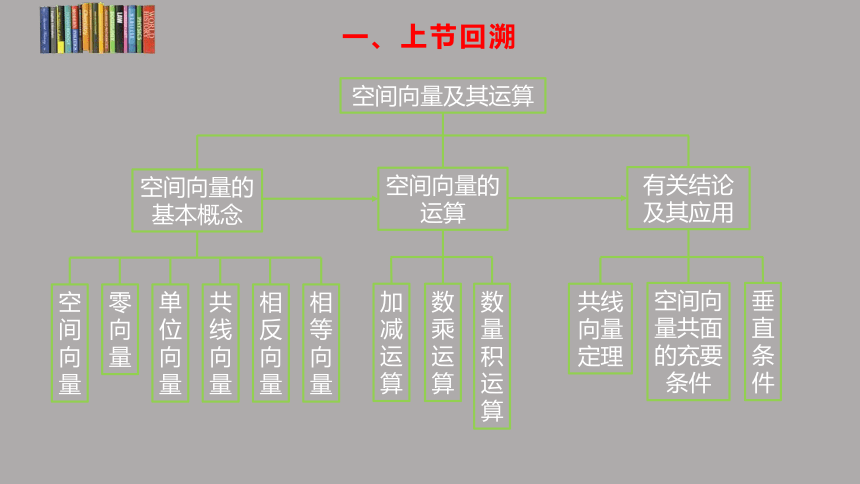
一、上节回溯
一、上节回溯
空间向量及其运算
空间向量的
基本概念
空间向量的
运算
有关结论
及其应用
零向量
空间向量
单位向量
共线向量
相反向量
相等向量
加减运算
数乘运算
数量积运算
共线向量定理
空间向量共面的充要条件
垂直条件
二、知识讲解
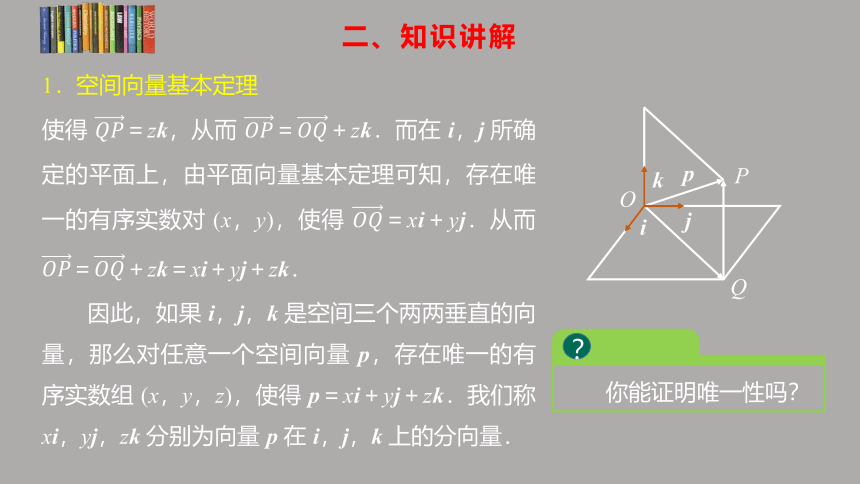
1.空间向量基本定理
如图,设 i,j,k 是空间中三个两两垂直的向量,且表示它们的有向线段有公共起点 O.对于任意一个空间向量 p=,设 为 在 i,j 所确定的平面上的投影向量,则 =+.又向量 ,k 共线,因此存在唯一的实数 z,
O
Q
P
j
i
k
p
二、知识讲解
使得 =zk,从而 =+zk.而在 i,j 所确定的平面上,由平面向量基本定理可知,存在唯一的有序实数对 (x,y),使得 =xi+yj.从而 =+zk=xi+yj+zk.
因此,如果 i,j,k 是空间三个两两垂直的向量,那么对任意一个空间向量 p,存在唯一的有序实数组 (x,y,z),使得 p=xi+yj+zk.我们称 xi,yj,zk 分别为向量 p 在 i,j,k 上的分向量.
O
Q
P
j
i
k
p
你能证明唯一性吗?
?
1.空间向量基本定理
定理 如果三个向量 a,b,c 不共面,那么对任意一个空间向量 p,存在唯一的有序实数组 (x,y,z),使得
p=xa+yb+zc.
二、知识讲解
在空间中,如果用任意三个不共面的向量 a,b,c 代替两两垂直的向量 i,j,k,你能得出类似的结论吗?
探究
1.空间向量基本定理
由此可知,如果三个向量 a,b,c 不共面,那么所有空间向量组成的集合就是 {p | p=xa+yb+zc,x,y,z∈R}.这个集合可看作由向量 a,b,c 生成的,我们把 {a,b,c} 叫做空间的一个基底(base),a,b,c 都叫做基向量(base vectors).空间中任意三个不共面的向量都可以构成空间的一个基底.
特别地,如果空间的一个基底中的三个基向量两两垂直,且长度都为 1,那么这个基底叫做单位正交基底,常用 {i,j,k} 表示.由空间向量基本定理可知,对空间中的任意向量 a,均可以分解为三个向量 xi,yj,zk,使 a=xi+yj+zk.像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
二、知识讲解
例1 如图,M 是四面体 OABC的棱 BC 的中点,点 N 在线段 OM 上,点 P 在线段 AN 上,且 MN=ON,AP=AN,用向量 ,, 表示.
分析:,, 是三个不共面的向量,它们构成空间的一个基底 {,,}, 可以用基底 {,,} 表示出来.
二、知识讲解
O
A
B
C
P
N
M
例2 如图,在平行六面体 ABCD-A1B1C1D1 中,AB=4,AD=4,AA1=5,∠DAB=60°,∠BAA1=60°,∠DAA1=60°,M,N 分别为 D1C1,C1B1 的中点.求证 MN⊥AC1.
二、知识讲解
分析:要证 MN⊥AC1,只需证明 · =0.由已知,{,,} 可构成空间的一个基底.把 和 分别用基底表示,然后计算 · 即可.
A
B
C
D
A1
B1
C1
D1
M
N
2.利用基向量解决几何问题
例3 如图,正方体 ABCD-A′B′C′D′的棱长为 1,E,F,G 分别为 C′D′,A′D′,D′D 的中点.
(1)求证:EF∥AC;
(2)求 CE 与 AG 所成角的余弦值.
分析:(1)要证明 EF∥AC,只需证明 与 共线.设 =i,=j,=k,则 {i,j,k} 构成空间的一个单位正交基底,把 和 分别用基向量表示,作相应的运算证明它们共线即可.(2)要求 CE 与 AG 所成角的余弦值,只需求 , 所成角的余弦值即可.
二、知识讲解
A
B
C
D
A′
B′
C′
D′
F
E
G
三、小结
空间向量基本定理
基底
基向量
单位正交基底
1.已知 {a,b,c} 是空间的一个基底,从 a,b,c 中选哪一个向量,一定可以与向量 p=a+b,q=a-b 构成空间的另一个基底?
答案:c 向量.
2.已知 O,A,B,C为空间的四个点,且向量 ,, 不构成空间的一个基底,那么点 O,A,B,C 是否共面?
答案:共面.
四、练习
3.如图,已知平行六面体 OABC-O′A′B′C′,点 G 是侧面 BB′C′C的中心,且=a,=b,=c .
(1){a,b,c} 是否构成空间的一个基底?
(2)如果 {a,b,c} 构成空间的一个基底,那么用它表示下列向量:,,,.
答案:(1)是;
(2)=a+b+c;=-b+c;
=a-b+c;=a+b+c.
四、练习
A
B
C
A′
B′
C′
O′
O
G
4.如图,在平行六面体 ABCD-A′B′C′D′ 中,AB=2,AD=2,AA′=3,∠BAD=∠BAA′=∠DAA′=60°.求 BC′ 与 CA′ 所成角的余弦值.
二、知识讲解
答案:0.
A
B
C
D
A′
B′
C′
D′
5.如图,已知正方体 ABCD-A′B′C′D′ ,CD′ 和
DC′ 相交于点 O,连接 AO,求证 AO⊥CD′.
答案:设 =a,=b,=c,且 |a|=|b|=
|c|=t,所以 =+=(+)+=
(a+b)+=a+b+c,==-a+c,
所以 · =0,所以 AO⊥CD′.
四、练习
A
B
C
A′
B′
C′
D′
D
O
1.2 空间向量基本定理
第一章 空间向量与立体几何
目录
二、知识讲解
三、小结
四、练习
一、上节回溯
一、上节回溯
空间向量及其运算
空间向量的
基本概念
空间向量的
运算
有关结论
及其应用
零向量
空间向量
单位向量
共线向量
相反向量
相等向量
加减运算
数乘运算
数量积运算
共线向量定理
空间向量共面的充要条件
垂直条件
二、知识讲解
1.空间向量基本定理
如图,设 i,j,k 是空间中三个两两垂直的向量,且表示它们的有向线段有公共起点 O.对于任意一个空间向量 p=,设 为 在 i,j 所确定的平面上的投影向量,则 =+.又向量 ,k 共线,因此存在唯一的实数 z,
O
Q
P
j
i
k
p
二、知识讲解
使得 =zk,从而 =+zk.而在 i,j 所确定的平面上,由平面向量基本定理可知,存在唯一的有序实数对 (x,y),使得 =xi+yj.从而 =+zk=xi+yj+zk.
因此,如果 i,j,k 是空间三个两两垂直的向量,那么对任意一个空间向量 p,存在唯一的有序实数组 (x,y,z),使得 p=xi+yj+zk.我们称 xi,yj,zk 分别为向量 p 在 i,j,k 上的分向量.
O
Q
P
j
i
k
p
你能证明唯一性吗?
?
1.空间向量基本定理
定理 如果三个向量 a,b,c 不共面,那么对任意一个空间向量 p,存在唯一的有序实数组 (x,y,z),使得
p=xa+yb+zc.
二、知识讲解
在空间中,如果用任意三个不共面的向量 a,b,c 代替两两垂直的向量 i,j,k,你能得出类似的结论吗?
探究
1.空间向量基本定理
由此可知,如果三个向量 a,b,c 不共面,那么所有空间向量组成的集合就是 {p | p=xa+yb+zc,x,y,z∈R}.这个集合可看作由向量 a,b,c 生成的,我们把 {a,b,c} 叫做空间的一个基底(base),a,b,c 都叫做基向量(base vectors).空间中任意三个不共面的向量都可以构成空间的一个基底.
特别地,如果空间的一个基底中的三个基向量两两垂直,且长度都为 1,那么这个基底叫做单位正交基底,常用 {i,j,k} 表示.由空间向量基本定理可知,对空间中的任意向量 a,均可以分解为三个向量 xi,yj,zk,使 a=xi+yj+zk.像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
二、知识讲解
例1 如图,M 是四面体 OABC的棱 BC 的中点,点 N 在线段 OM 上,点 P 在线段 AN 上,且 MN=ON,AP=AN,用向量 ,, 表示.
分析:,, 是三个不共面的向量,它们构成空间的一个基底 {,,}, 可以用基底 {,,} 表示出来.
二、知识讲解
O
A
B
C
P
N
M
例2 如图,在平行六面体 ABCD-A1B1C1D1 中,AB=4,AD=4,AA1=5,∠DAB=60°,∠BAA1=60°,∠DAA1=60°,M,N 分别为 D1C1,C1B1 的中点.求证 MN⊥AC1.
二、知识讲解
分析:要证 MN⊥AC1,只需证明 · =0.由已知,{,,} 可构成空间的一个基底.把 和 分别用基底表示,然后计算 · 即可.
A
B
C
D
A1
B1
C1
D1
M
N
2.利用基向量解决几何问题
例3 如图,正方体 ABCD-A′B′C′D′的棱长为 1,E,F,G 分别为 C′D′,A′D′,D′D 的中点.
(1)求证:EF∥AC;
(2)求 CE 与 AG 所成角的余弦值.
分析:(1)要证明 EF∥AC,只需证明 与 共线.设 =i,=j,=k,则 {i,j,k} 构成空间的一个单位正交基底,把 和 分别用基向量表示,作相应的运算证明它们共线即可.(2)要求 CE 与 AG 所成角的余弦值,只需求 , 所成角的余弦值即可.
二、知识讲解
A
B
C
D
A′
B′
C′
D′
F
E
G
三、小结
空间向量基本定理
基底
基向量
单位正交基底
1.已知 {a,b,c} 是空间的一个基底,从 a,b,c 中选哪一个向量,一定可以与向量 p=a+b,q=a-b 构成空间的另一个基底?
答案:c 向量.
2.已知 O,A,B,C为空间的四个点,且向量 ,, 不构成空间的一个基底,那么点 O,A,B,C 是否共面?
答案:共面.
四、练习
3.如图,已知平行六面体 OABC-O′A′B′C′,点 G 是侧面 BB′C′C的中心,且=a,=b,=c .
(1){a,b,c} 是否构成空间的一个基底?
(2)如果 {a,b,c} 构成空间的一个基底,那么用它表示下列向量:,,,.
答案:(1)是;
(2)=a+b+c;=-b+c;
=a-b+c;=a+b+c.
四、练习
A
B
C
A′
B′
C′
O′
O
G
4.如图,在平行六面体 ABCD-A′B′C′D′ 中,AB=2,AD=2,AA′=3,∠BAD=∠BAA′=∠DAA′=60°.求 BC′ 与 CA′ 所成角的余弦值.
二、知识讲解
答案:0.
A
B
C
D
A′
B′
C′
D′
5.如图,已知正方体 ABCD-A′B′C′D′ ,CD′ 和
DC′ 相交于点 O,连接 AO,求证 AO⊥CD′.
答案:设 =a,=b,=c,且 |a|=|b|=
|c|=t,所以 =+=(+)+=
(a+b)+=a+b+c,==-a+c,
所以 · =0,所以 AO⊥CD′.
四、练习
A
B
C
A′
B′
C′
D′
D
O
