人教A版(2019)选择性必修第一册1.1空间向量及其运算 课件(共20张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册1.1空间向量及其运算 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 795.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-24 22:35:03 | ||
图片预览






文档简介
(共20张PPT)
1.1 空间向量及其运算
第一章 空间向量与立体几何
目录
一、知识讲解
二、小结
三、练习
1.空间向量的相关概念
与平面向量一样,在空间,我们把具有大小和方向的量叫做空间向量(space vector),空间向量的大小叫做空间向量的长度或模(modulus).空间向量用字母 a,b,c表示.
我们规定,长度为 0 的向量叫做零向量(zero vector),记为 0.当有向线段的起点 A 与终点 B 重合时,模为 1 的向量叫做单位向量(unit vector).与向量 a 长度相等而方向相反的向量,叫做 a 的相反向量,记为-a.
一、知识讲解
a
A
B
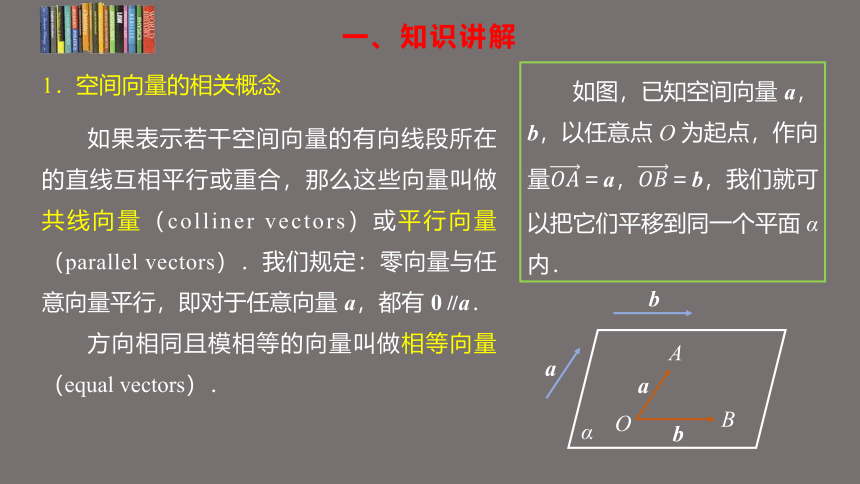
如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量(colliner vectors)或平行向量(parallel vectors).我们规定:零向量与任意向量平行,即对于任意向量 a,都有 0∥a.
方向相同且模相等的向量叫做相等向量(equal vectors).
一、知识讲解
如图,已知空间向量 a,b,以任意点 O 为起点,作向量=a,=b,我们就可以把它们平移到同一个平面 α内.
a
A
B
b
a
b
O
α
1.空间向量的相关概念
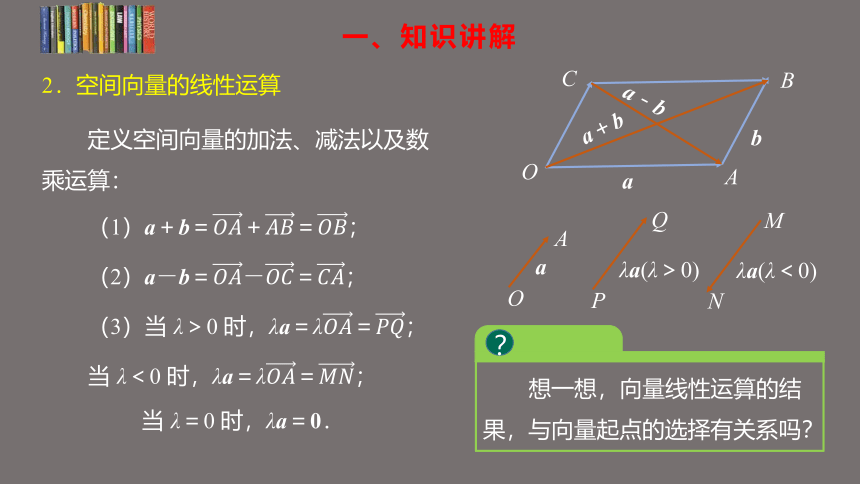
定义空间向量的加法、减法以及数乘运算:
(1)a+b=+=;
(2)a-b=-=;
(3)当 λ>0 时,λa=λ=;
当 λ<0 时,λa=λ=;
当 λ=0 时,λa=0.
一、知识讲解
想一想,向量线性运算的结果,与向量起点的选择有关系吗?
?
O
A
B
C
a
b
a-b
a+b
a
O
A
λa(λ>0)
P
Q
λa(λ<0)
N
M
2.空间向量的线性运算
空间向量的线性运算满足以下运算律(其中 λ,μ∈R):
交换律:a+b=b+a;
结合律:(a+b)+c=a+(b+c),
λ(μa)=(λμ)a;
分配律:(λ+μ)a=λa+μa,
λ(a+b)=λa+λb.
一、知识讲解
你能证明这些运算律吗?证明结合律时,与证明平面向量的结合律有什么不同?
?
2.空间向量的线性运算
一、知识讲解
如图,在平行六面体 ABCD-A′B′C′D′ 中,分别标出 ++,++ 表示的向 量.从中你能体会向量加法运算的交换律和结 合律吗?一般地,三个不共面的向量的和与这 三个向量有什么关系?
探究
A
B
C
D
A′
B′
C′
D′
对任意两个空间向量 a,b (b≠0),a∥b的充要条件是存在实数 λ,使a=λb.
如图,O 是直线 l 上一点,在直线 l 上取非零向量 a,则对于直线 l 上任意一点 P,由数乘向量的定义及向量共线的充要条件可知,存在实数 λ,使得 =λa.我们把与向量 a 平行的非零向量称为直线 l 的方向向量(direction vector).
一、知识讲解
对任意两个空间向量 a 与 b,如果 a=λb(λ∈R), a 与 b 有什么位置关系?反过来,a 与 b 有什么位置关系时,a=λb?
探究
a
O
P
a
l
3.空间向量的共线与共面
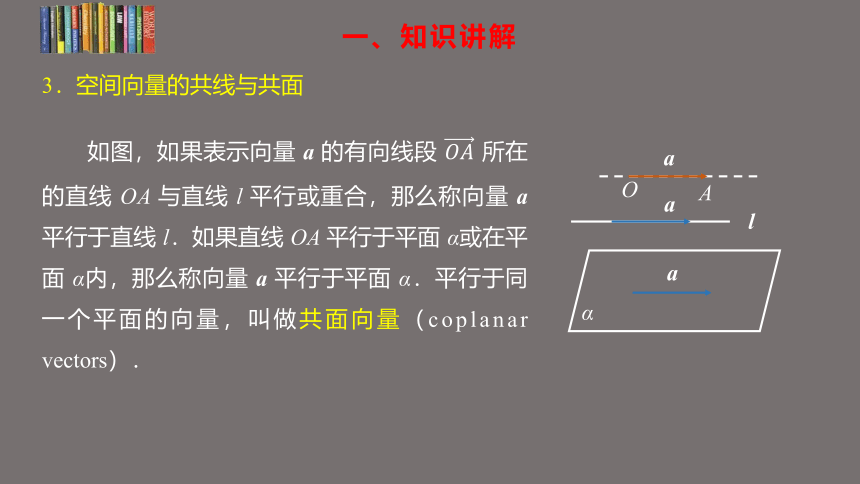
如图,如果表示向量 a 的有向线段 所在的直线 OA 与直线 l 平行或重合,那么称向量 a 平行于直线 l.如果直线 OA 平行于平面 α或在平面 α内,那么称向量 a 平行于平面 α.平行于同一个平面的向量,叫做共面向量(coplanar vectors).
一、知识讲解
a
O
A
a
l
a
α
3.空间向量的共线与共面
如果两个向量 a,b 不共线,那么向量 p 与向量 a,b 共面的充要条件是存在唯一的有序实数对 (x,y),使 p=xa+yb.
一、知识讲解
对平面内任意两个不共线向量 a,b,由平面向量基本定理可知,这个平面内的任意一个向量 p 可以写成 p=xa+yb,其中 (x,y) 是唯一确定的有序实数对.对两个不共线的空间向量 a,b,如果 p=xa+yb,那么向量 p 与向量 a,b 有什么位置关系?反过来,向量 p 与向量 a,b 有什么位置关系时,p=xa+yb?
探究
3.空间向量的共线与共面
例1 如图,已知平行四边形 ABCD,过平面 AC 外一点 O 作射线 OA,OB,OC,OD,在四条射线上分别取点 E,F,G,H,使 ====k.求证:E,F,G,H 四点共面.
分析:欲证 E,F,G,H 四点共面,只需证明 ,, 共面.而由已知 ,, 共面,可以利用向量运算由 ,, 共面的表达式推得 ,, 共面的表达式.
一、知识讲解
O
A
B
C
D
E
F
G
H
已知两个非零向量 a,b,则 |a||b|cos叫做 a,b 的数量积(inner product),记作 a· b.即 a· b=|a||b|cos.
特别地,零向量与任意向量的数量积为 0.
由向量的数量积定义,可以得到:
a⊥b a· b=0;
a· a=|a||a|cos=|a|2.
4.空间向量的数量积运算
一、知识讲解
在平面向量的学习中,我们学习了向量的投影.类似地,在空间,向量 a 向向量 b 的投影有什么意义?向量 a 向直线 l 的投影呢?向量 a 向平面 β 的投影呢?
?
思考
空间向量的数量积满足如下的运算律:
(λa) · b=λ(a · b),λ∈R;
a · b=b · a(交换律);
(a+b) · c=a · c+b · c(分配律).
一、知识讲解
4.空间向量的数量积运算
一、知识讲解
(1)对于三个均不为 0 的数 a,b,c,若 ab=ac,则 b=c .对于向量 a,b,c,由 a· b=a· c,你能得到 b=c 吗?如果不能,请举出反例.
(2)对于三个均不为 0 的数 a,b,c,若 ab=c,则 a=(或 b=).对于向量 a,b,若 a· b=k,能不能写成 a=(或 b=)的形式?
(3)对于三个均不为 0 的数 a,b,c,有 (ab)c=a(bc).对于向量 a,b,c,由 (a· b)c=a(b· c)成立吗?为什么?
?
思考
例2 如图,在平行六面体 ABCD-A′B′C′D′中,AB=5,AD=3,AA′=7,∠BAD=60°,∠BAA′=∠DAA′= 45°.求:
(1)· ;(2)AC′ 的长(精确到 0.1).
解:(1)· =||||cos<,>=7.5;(2)||2=(++)2=98+56,所以 AC′≈13.3.
一、知识讲解
A
B
C
D
A′
B′
C′
D′
例3 如图,m,n 是平面 α 内的两条相交直线.如果 l⊥m,l⊥n ,求证:l⊥α.
分析:要证明 l⊥α,就是要证明 l 垂直于 α 内的任意一条直线 g(直线与平面垂直的定义).如果我们能在 g和 m,n 之间建立某种联系,并由l⊥m,l⊥n,得到 l⊥g,那么就能解决此问题.
一、知识讲解
l
m
n
n
m
g
l
α
g
例 3 即为直线与平面垂直的判定定理的证明过程.尝试用综合几何方法证明这个定理,并比较两种方法,你能从中体会到向量方法的优越性吗?
?
二、小结
空间向量及其运算
空间向量的
基本概念
空间向量的
运算
有关结论
及其应用
零向量
空间向量
单位向量
共线向量
相反向量
相等向量
加减运算
数乘运算
数量积运算
共线向量定理
空间向量共面的充要条件
垂直条件
1.举出一些表示三个不同在一个平面内的向量的实例.
答案:三棱锥的三条侧棱;长方体中,从同一点引出的三条边等等.
2.如图,在平行六面体 ABCD-A′B′C′D′ 中,用 ,, 表示 , 及 .
答案:=+=-+(+)=+-;
=+=(+)+=(-+)+
=+;
=+=(+)+=(-+)+
=+.
三、练习
A
B
C
A′
B′
C′
D′
D
3.如图,在正三棱柱 ABC-A1B1C1中,若 AB=BB1,
则 AB1 与 BC1 所成角的大小为( ).
(A) 60° (B) 90° (C)105° (D)75°
答案:B.
4.如图,正方体 ABCD-A′B′C′D′ 的棱长为 1,
设 =a,=b,=c ,求:
(1)a· (b+c);(2)a· (a+b+c) ;
(3)(a+b)· (b+c).
答案:(1)0;(2)1;(3)1.
三、练习
A
B
C
A1
B1
C1
A
B
C
A′
B′
C′
D′
D
a
b
c
5.如图,线段 AB,BD 在平面 α内,BD⊥AB,AC⊥α,且 AB=a,BD=b,AC=c.求 C,D 两点间的距离.
答案:由已知可得 =++,利用数量积的性质即可得出 C,D 两点间的距离为 .
三、练习
A
B
D
C
a
b
c
α
1.1 空间向量及其运算
第一章 空间向量与立体几何
目录
一、知识讲解
二、小结
三、练习
1.空间向量的相关概念
与平面向量一样,在空间,我们把具有大小和方向的量叫做空间向量(space vector),空间向量的大小叫做空间向量的长度或模(modulus).空间向量用字母 a,b,c表示.
我们规定,长度为 0 的向量叫做零向量(zero vector),记为 0.当有向线段的起点 A 与终点 B 重合时,模为 1 的向量叫做单位向量(unit vector).与向量 a 长度相等而方向相反的向量,叫做 a 的相反向量,记为-a.
一、知识讲解
a
A
B
如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量(colliner vectors)或平行向量(parallel vectors).我们规定:零向量与任意向量平行,即对于任意向量 a,都有 0∥a.
方向相同且模相等的向量叫做相等向量(equal vectors).
一、知识讲解
如图,已知空间向量 a,b,以任意点 O 为起点,作向量=a,=b,我们就可以把它们平移到同一个平面 α内.
a
A
B
b
a
b
O
α
1.空间向量的相关概念
定义空间向量的加法、减法以及数乘运算:
(1)a+b=+=;
(2)a-b=-=;
(3)当 λ>0 时,λa=λ=;
当 λ<0 时,λa=λ=;
当 λ=0 时,λa=0.
一、知识讲解
想一想,向量线性运算的结果,与向量起点的选择有关系吗?
?
O
A
B
C
a
b
a-b
a+b
a
O
A
λa(λ>0)
P
Q
λa(λ<0)
N
M
2.空间向量的线性运算
空间向量的线性运算满足以下运算律(其中 λ,μ∈R):
交换律:a+b=b+a;
结合律:(a+b)+c=a+(b+c),
λ(μa)=(λμ)a;
分配律:(λ+μ)a=λa+μa,
λ(a+b)=λa+λb.
一、知识讲解
你能证明这些运算律吗?证明结合律时,与证明平面向量的结合律有什么不同?
?
2.空间向量的线性运算
一、知识讲解
如图,在平行六面体 ABCD-A′B′C′D′ 中,分别标出 ++,++ 表示的向 量.从中你能体会向量加法运算的交换律和结 合律吗?一般地,三个不共面的向量的和与这 三个向量有什么关系?
探究
A
B
C
D
A′
B′
C′
D′
对任意两个空间向量 a,b (b≠0),a∥b的充要条件是存在实数 λ,使a=λb.
如图,O 是直线 l 上一点,在直线 l 上取非零向量 a,则对于直线 l 上任意一点 P,由数乘向量的定义及向量共线的充要条件可知,存在实数 λ,使得 =λa.我们把与向量 a 平行的非零向量称为直线 l 的方向向量(direction vector).
一、知识讲解
对任意两个空间向量 a 与 b,如果 a=λb(λ∈R), a 与 b 有什么位置关系?反过来,a 与 b 有什么位置关系时,a=λb?
探究
a
O
P
a
l
3.空间向量的共线与共面
如图,如果表示向量 a 的有向线段 所在的直线 OA 与直线 l 平行或重合,那么称向量 a 平行于直线 l.如果直线 OA 平行于平面 α或在平面 α内,那么称向量 a 平行于平面 α.平行于同一个平面的向量,叫做共面向量(coplanar vectors).
一、知识讲解
a
O
A
a
l
a
α
3.空间向量的共线与共面
如果两个向量 a,b 不共线,那么向量 p 与向量 a,b 共面的充要条件是存在唯一的有序实数对 (x,y),使 p=xa+yb.
一、知识讲解
对平面内任意两个不共线向量 a,b,由平面向量基本定理可知,这个平面内的任意一个向量 p 可以写成 p=xa+yb,其中 (x,y) 是唯一确定的有序实数对.对两个不共线的空间向量 a,b,如果 p=xa+yb,那么向量 p 与向量 a,b 有什么位置关系?反过来,向量 p 与向量 a,b 有什么位置关系时,p=xa+yb?
探究
3.空间向量的共线与共面
例1 如图,已知平行四边形 ABCD,过平面 AC 外一点 O 作射线 OA,OB,OC,OD,在四条射线上分别取点 E,F,G,H,使 ====k.求证:E,F,G,H 四点共面.
分析:欲证 E,F,G,H 四点共面,只需证明 ,, 共面.而由已知 ,, 共面,可以利用向量运算由 ,, 共面的表达式推得 ,, 共面的表达式.
一、知识讲解
O
A
B
C
D
E
F
G
H
已知两个非零向量 a,b,则 |a||b|cos
特别地,零向量与任意向量的数量积为 0.
由向量的数量积定义,可以得到:
a⊥b a· b=0;
a· a=|a||a|cos
4.空间向量的数量积运算
一、知识讲解
在平面向量的学习中,我们学习了向量的投影.类似地,在空间,向量 a 向向量 b 的投影有什么意义?向量 a 向直线 l 的投影呢?向量 a 向平面 β 的投影呢?
?
思考
空间向量的数量积满足如下的运算律:
(λa) · b=λ(a · b),λ∈R;
a · b=b · a(交换律);
(a+b) · c=a · c+b · c(分配律).
一、知识讲解
4.空间向量的数量积运算
一、知识讲解
(1)对于三个均不为 0 的数 a,b,c,若 ab=ac,则 b=c .对于向量 a,b,c,由 a· b=a· c,你能得到 b=c 吗?如果不能,请举出反例.
(2)对于三个均不为 0 的数 a,b,c,若 ab=c,则 a=(或 b=).对于向量 a,b,若 a· b=k,能不能写成 a=(或 b=)的形式?
(3)对于三个均不为 0 的数 a,b,c,有 (ab)c=a(bc).对于向量 a,b,c,由 (a· b)c=a(b· c)成立吗?为什么?
?
思考
例2 如图,在平行六面体 ABCD-A′B′C′D′中,AB=5,AD=3,AA′=7,∠BAD=60°,∠BAA′=∠DAA′= 45°.求:
(1)· ;(2)AC′ 的长(精确到 0.1).
解:(1)· =||||cos<,>=7.5;(2)||2=(++)2=98+56,所以 AC′≈13.3.
一、知识讲解
A
B
C
D
A′
B′
C′
D′
例3 如图,m,n 是平面 α 内的两条相交直线.如果 l⊥m,l⊥n ,求证:l⊥α.
分析:要证明 l⊥α,就是要证明 l 垂直于 α 内的任意一条直线 g(直线与平面垂直的定义).如果我们能在 g和 m,n 之间建立某种联系,并由l⊥m,l⊥n,得到 l⊥g,那么就能解决此问题.
一、知识讲解
l
m
n
n
m
g
l
α
g
例 3 即为直线与平面垂直的判定定理的证明过程.尝试用综合几何方法证明这个定理,并比较两种方法,你能从中体会到向量方法的优越性吗?
?
二、小结
空间向量及其运算
空间向量的
基本概念
空间向量的
运算
有关结论
及其应用
零向量
空间向量
单位向量
共线向量
相反向量
相等向量
加减运算
数乘运算
数量积运算
共线向量定理
空间向量共面的充要条件
垂直条件
1.举出一些表示三个不同在一个平面内的向量的实例.
答案:三棱锥的三条侧棱;长方体中,从同一点引出的三条边等等.
2.如图,在平行六面体 ABCD-A′B′C′D′ 中,用 ,, 表示 , 及 .
答案:=+=-+(+)=+-;
=+=(+)+=(-+)+
=+;
=+=(+)+=(-+)+
=+.
三、练习
A
B
C
A′
B′
C′
D′
D
3.如图,在正三棱柱 ABC-A1B1C1中,若 AB=BB1,
则 AB1 与 BC1 所成角的大小为( ).
(A) 60° (B) 90° (C)105° (D)75°
答案:B.
4.如图,正方体 ABCD-A′B′C′D′ 的棱长为 1,
设 =a,=b,=c ,求:
(1)a· (b+c);(2)a· (a+b+c) ;
(3)(a+b)· (b+c).
答案:(1)0;(2)1;(3)1.
三、练习
A
B
C
A1
B1
C1
A
B
C
A′
B′
C′
D′
D
a
b
c
5.如图,线段 AB,BD 在平面 α内,BD⊥AB,AC⊥α,且 AB=a,BD=b,AC=c.求 C,D 两点间的距离.
答案:由已知可得 =++,利用数量积的性质即可得出 C,D 两点间的距离为 .
三、练习
A
B
D
C
a
b
c
α
