人教A版(2019)选择性必修第一册3.3抛物线计算(基础)学案(Word版含答案)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册3.3抛物线计算(基础)学案(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 158.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 00:00:00 | ||
图片预览


文档简介
《圆锥曲线》专题21-1 抛物线计算(基础)
(4套,3页,含答案)
知识点:
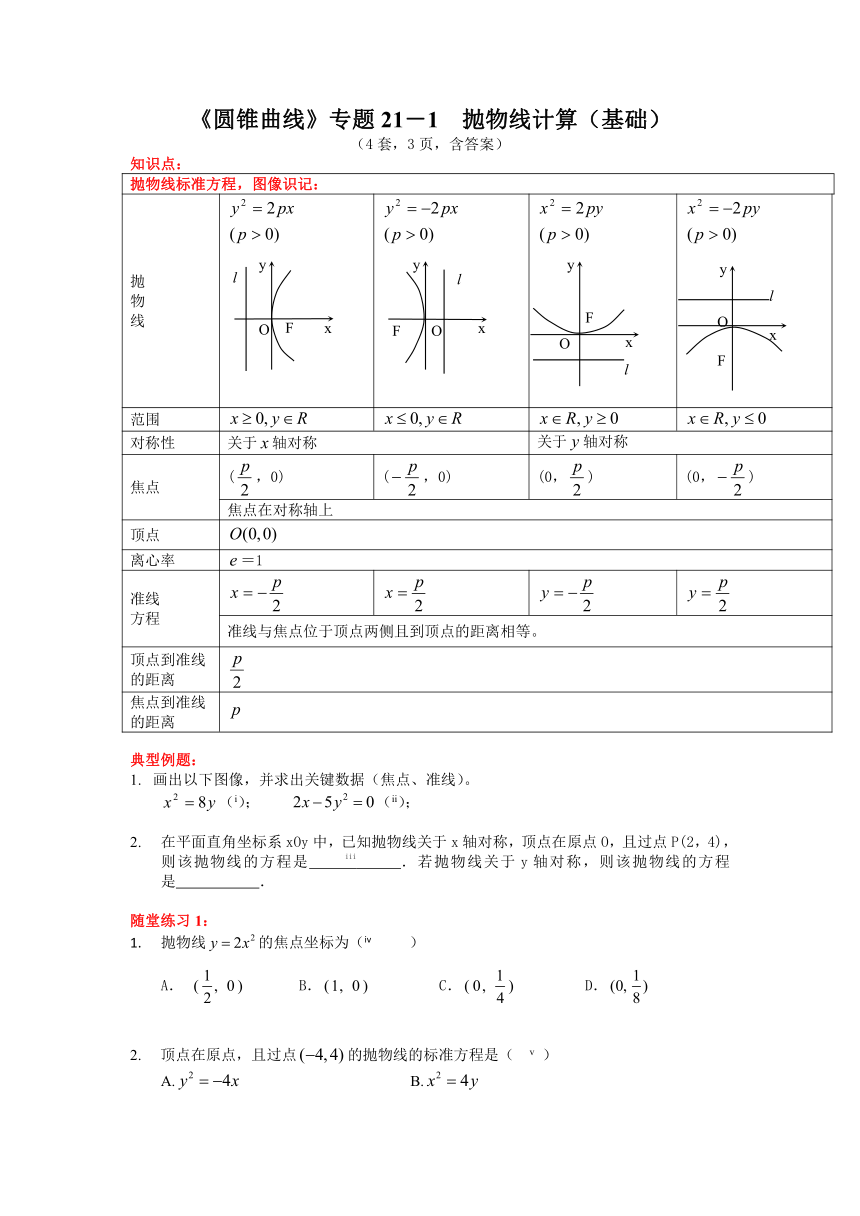
抛物线标准方程,图像识记:
抛 物 线
范围
对称性 关于轴对称 关于轴对称
焦点 (,0) (,0) (0,) (0,)
焦点在对称轴上
顶点
离心率 =1
准线 方程
准线与焦点位于顶点两侧且到顶点的距离相等。
顶点到准线的距离
焦点到准线的距离
典型例题:
画出以下图像,并求出关键数据(焦点、准线)。
([endnoteRef:0]); ([endnoteRef:1]); [0: ] [1: ]
在平面直角坐标系xOy中,已知抛物线关于x轴对称,顶点在原点O,且过点P(2,4),则该抛物线的方程是 [endnoteRef:2] .若抛物线关于y轴对称,则该抛物线的方程是 . [2: 答案:,;]
随堂练习1:
抛物线的焦点坐标为([endnoteRef:3] )
A. B. C. D.
[3: 答案:D;]
顶点在原点,且过点的抛物线的标准方程是( [endnoteRef:4] )
A. B.
C.或 D. 或 [4: 答案:C;]
抛物线的准线方程y=2,则a的值为了( [endnoteRef:5] )
A. B.-8 C. D.8 [5: 答案:C;]
随堂练习2——结合其他曲线:
已知抛物线y2=2px(p>0)的准线与圆x2+y2-6x-7=0相切,则p的值为( [endnoteRef:6] )
A. B.1 C.2 D.4 [6: 答案: C;
解析: 圆的标准方程为(x-3)2+y2=16,圆心(3,0)到抛物线准线x=-的距离为4,
∴=1,∴p=2,故选C.]
若抛物线的焦点与椭圆的右焦点重合,则P的值为( [endnoteRef:7] )
A.-2 B.2 C.-4 D.4 [7: 答案:D;]
抛物线的焦点到双曲线的渐近线的距离是( [endnoteRef:8] )
A. B. C. D.
[8: 答案:D;]
《圆锥曲线》专题21-2 抛物线计算(基础)
根据下列抛物线的方程,分别求出其焦点坐标和准线方程.
(1)y2=-4x;(2)2y2-x=0.[endnoteRef:9] [9: 答案:(-1,0),x=1,,x=-;
解析:
]
若直线ax-y+1=0经过抛物线y2=4x的焦点,则实数a=_____[endnoteRef:10]___. [10: 答案: -1;
解析: 由题意知抛物线的焦点为(1,0)
代入直线方程得a×1-0+1=0,∴a=-1.
]
抛物线的焦点与双曲线-=1的焦点重合,则抛物线的准线方程是___[endnoteRef:11]_____. [11: 答案: x=±5;
解析: 在双曲线-=1中,a2=16,b2=9,
∴c===5,
∴焦点坐标是F1(-5,0),F2(5,0).
当抛物线焦点是F1(-5,0)时,=5,
准线方程是x=5;
当抛物线焦点是F2(5,0)时,=5,
准线方程是x=-5,
所以应填x=-5或x=5.]
已知圆x2+y2+8x+2y-8=0与抛物线y2=2px的准线相切,则p=____[endnoteRef:12]____. [12: 答案:-2或18;]
《圆锥曲线》专题21-3 抛物线计算(基础)
已知抛物线的焦点在直线-4=0上,则此抛物线的标准方程是( [endnoteRef:13] )
?A. B. ?C. 或 ?D. 或 [13: 答案:C;]
抛物线y=-x2的准线方程为( [endnoteRef:14] )
A.x= B.x=1 C.y=1 D.y=2 [14: 答案:C;
解析: 抛物线的标准方程为x2=-4y,
准线方程为y=1.
]
已知抛物线的准线与圆相切,则的值为[endnoteRef:15] .
[15: 答案:2;]
以双曲线-=1的右顶点为焦点的抛物线的标准方程为( [endnoteRef:16] )
A.y2=16x B.y2=-16x C.y2=8x D.y2=-8x [16: 答案:A;
解析: 由双曲线方程-=1,
可知其焦点在x轴上,由a2=16,得a=4,
∴该双曲线右顶点的坐标是(4,0),
∴抛物线的焦点为F(4,0).
设抛物线的标准方程为y2=2px(p>0),
则由=4,得p=8,
故所求抛物线的标准方程为y2=16x.故选A.
]
《圆锥曲线》专题21-4 抛物线计算(基础)
抛物线的焦点到准线的距离是( [endnoteRef:17] )
A. B C. D [17: 答案:B;]
抛物线的焦点坐标为 ( [endnoteRef:18] ) A. B. C. D. [18: 答案:A;]
已知抛物线y2=2px(p>0)的准线与圆x2+y2-4x-5=0相切,则p的值为___[endnoteRef:19]__.
[19: 答案:2;
解析:依题意,圆x2+y2-4x-5=0可化为(x-2)2+y2=32,圆心(2,0)到抛物线的准线x=-的距离等于圆的半径3,于是有2+=3,p=2.]
抛物线的焦点到双曲线的渐近线的距离是( [endnoteRef:20] )
A. B. C. D.
[20: 答案:D;]
(4套,3页,含答案)
知识点:
抛物线标准方程,图像识记:
抛 物 线
范围
对称性 关于轴对称 关于轴对称
焦点 (,0) (,0) (0,) (0,)
焦点在对称轴上
顶点
离心率 =1
准线 方程
准线与焦点位于顶点两侧且到顶点的距离相等。
顶点到准线的距离
焦点到准线的距离
典型例题:
画出以下图像,并求出关键数据(焦点、准线)。
([endnoteRef:0]); ([endnoteRef:1]); [0: ] [1: ]
在平面直角坐标系xOy中,已知抛物线关于x轴对称,顶点在原点O,且过点P(2,4),则该抛物线的方程是 [endnoteRef:2] .若抛物线关于y轴对称,则该抛物线的方程是 . [2: 答案:,;]
随堂练习1:
抛物线的焦点坐标为([endnoteRef:3] )
A. B. C. D.
[3: 答案:D;]
顶点在原点,且过点的抛物线的标准方程是( [endnoteRef:4] )
A. B.
C.或 D. 或 [4: 答案:C;]
抛物线的准线方程y=2,则a的值为了( [endnoteRef:5] )
A. B.-8 C. D.8 [5: 答案:C;]
随堂练习2——结合其他曲线:
已知抛物线y2=2px(p>0)的准线与圆x2+y2-6x-7=0相切,则p的值为( [endnoteRef:6] )
A. B.1 C.2 D.4 [6: 答案: C;
解析: 圆的标准方程为(x-3)2+y2=16,圆心(3,0)到抛物线准线x=-的距离为4,
∴=1,∴p=2,故选C.]
若抛物线的焦点与椭圆的右焦点重合,则P的值为( [endnoteRef:7] )
A.-2 B.2 C.-4 D.4 [7: 答案:D;]
抛物线的焦点到双曲线的渐近线的距离是( [endnoteRef:8] )
A. B. C. D.
[8: 答案:D;]
《圆锥曲线》专题21-2 抛物线计算(基础)
根据下列抛物线的方程,分别求出其焦点坐标和准线方程.
(1)y2=-4x;(2)2y2-x=0.[endnoteRef:9] [9: 答案:(-1,0),x=1,,x=-;
解析:
]
若直线ax-y+1=0经过抛物线y2=4x的焦点,则实数a=_____[endnoteRef:10]___. [10: 答案: -1;
解析: 由题意知抛物线的焦点为(1,0)
代入直线方程得a×1-0+1=0,∴a=-1.
]
抛物线的焦点与双曲线-=1的焦点重合,则抛物线的准线方程是___[endnoteRef:11]_____. [11: 答案: x=±5;
解析: 在双曲线-=1中,a2=16,b2=9,
∴c===5,
∴焦点坐标是F1(-5,0),F2(5,0).
当抛物线焦点是F1(-5,0)时,=5,
准线方程是x=5;
当抛物线焦点是F2(5,0)时,=5,
准线方程是x=-5,
所以应填x=-5或x=5.]
已知圆x2+y2+8x+2y-8=0与抛物线y2=2px的准线相切,则p=____[endnoteRef:12]____. [12: 答案:-2或18;]
《圆锥曲线》专题21-3 抛物线计算(基础)
已知抛物线的焦点在直线-4=0上,则此抛物线的标准方程是( [endnoteRef:13] )
?A. B. ?C. 或 ?D. 或 [13: 答案:C;]
抛物线y=-x2的准线方程为( [endnoteRef:14] )
A.x= B.x=1 C.y=1 D.y=2 [14: 答案:C;
解析: 抛物线的标准方程为x2=-4y,
准线方程为y=1.
]
已知抛物线的准线与圆相切,则的值为[endnoteRef:15] .
[15: 答案:2;]
以双曲线-=1的右顶点为焦点的抛物线的标准方程为( [endnoteRef:16] )
A.y2=16x B.y2=-16x C.y2=8x D.y2=-8x [16: 答案:A;
解析: 由双曲线方程-=1,
可知其焦点在x轴上,由a2=16,得a=4,
∴该双曲线右顶点的坐标是(4,0),
∴抛物线的焦点为F(4,0).
设抛物线的标准方程为y2=2px(p>0),
则由=4,得p=8,
故所求抛物线的标准方程为y2=16x.故选A.
]
《圆锥曲线》专题21-4 抛物线计算(基础)
抛物线的焦点到准线的距离是( [endnoteRef:17] )
A. B C. D [17: 答案:B;]
抛物线的焦点坐标为 ( [endnoteRef:18] ) A. B. C. D. [18: 答案:A;]
已知抛物线y2=2px(p>0)的准线与圆x2+y2-4x-5=0相切,则p的值为___[endnoteRef:19]__.
[19: 答案:2;
解析:依题意,圆x2+y2-4x-5=0可化为(x-2)2+y2=32,圆心(2,0)到抛物线的准线x=-的距离等于圆的半径3,于是有2+=3,p=2.]
抛物线的焦点到双曲线的渐近线的距离是( [endnoteRef:20] )
A. B. C. D.
[20: 答案:D;]
