人教B版(2019)必修第四册11.1.4 棱锥与棱台 教学设计(表格式)
文档属性
| 名称 | 人教B版(2019)必修第四册11.1.4 棱锥与棱台 教学设计(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 42.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 00:00:00 | ||
图片预览

文档简介
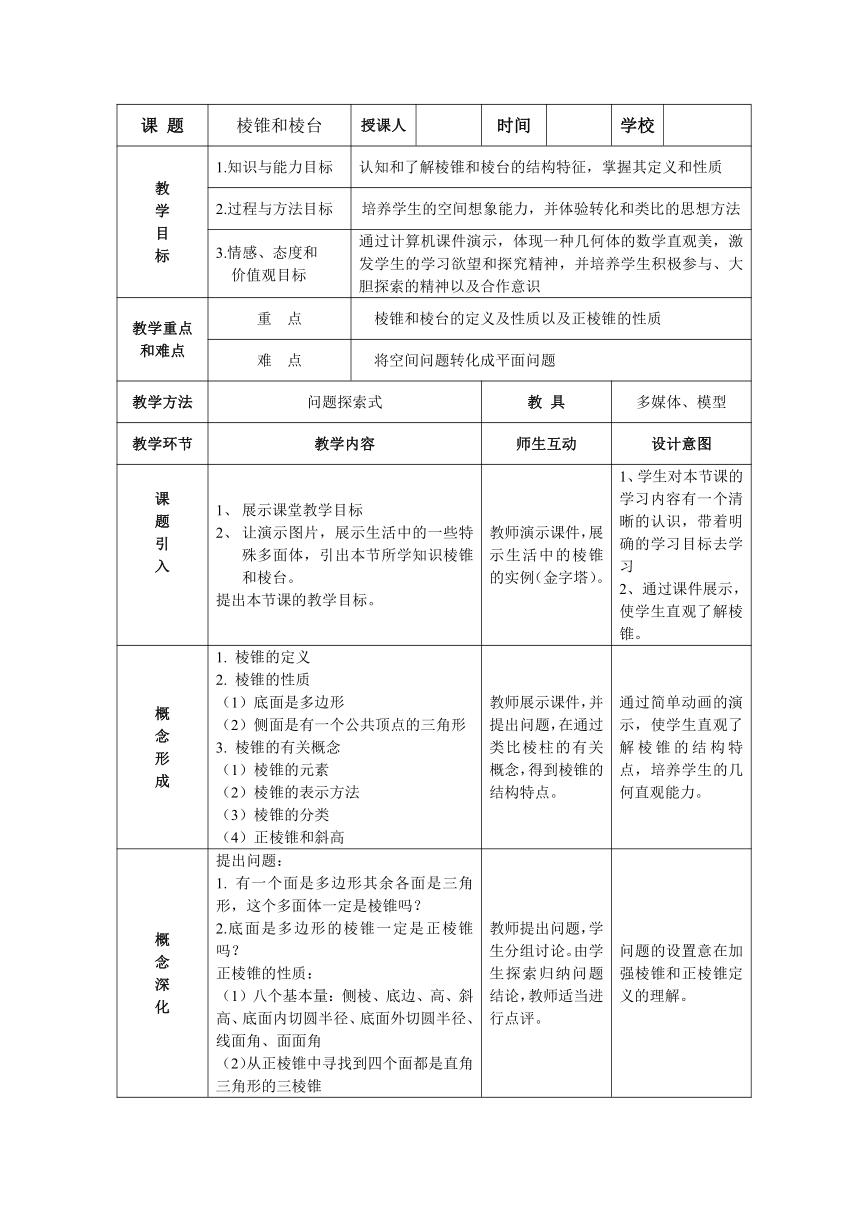
课 题 棱锥和棱台 授课人 时间 学校
教学目标 1.知识与能力目标 认知和了解棱锥和棱台的结构特征,掌握其定义和性质
2.过程与方法目标 培养学生的空间想象能力,并体验转化和类比的思想方法
3.情感、态度和价值观目标 通过计算机课件演示,体现一种几何体的数学直观美,激发学生的学习欲望和探究精神,并培养学生积极参与、大胆探索的精神以及合作意识
教学重点和难点 重 点 棱锥和棱台的定义及性质以及正棱锥的性质
难 点 将空间问题转化成平面问题
教学方法 问题探索式 教 具 多媒体、模型
教学环节 教学内容 师生互动 设计意图
课题引入 展示课堂教学目标让演示图片,展示生活中的一些特殊多面体,引出本节所学知识棱锥和棱台。提出本节课的教学目标。 教师演示课件,展示生活中的棱锥的实例(金字塔)。 1、学生对本节课的学习内容有一个清晰的认识,带着明确的学习目标去学习2、通过课件展示,使学生直观了解棱锥。
概念形成 1. 棱锥的定义2. 棱锥的性质(1)底面是多边形(2)侧面是有一个公共顶点的三角形3. 棱锥的有关概念(1)棱锥的元素(2)棱锥的表示方法(3)棱锥的分类(4)正棱锥和斜高 教师展示课件,并提出问题,在通过类比棱柱的有关概念,得到棱锥的结构特点。 通过简单动画的演示,使学生直观了解棱锥的结构特点,培养学生的几何直观能力。
概念深化 提出问题:1. 有一个面是多边形其余各面是三角形,这个多面体一定是棱锥吗?2.底面是多边形的棱锥一定是正棱锥吗?正棱锥的性质:(1)八个基本量:侧棱、底边、高、斜高、底面内切圆半径、底面外切圆半径、线面角、面面角(2)从正棱锥中寻找到四个面都是直角三角形的三棱锥 教师提出问题,学生分组讨论。由学生探索归纳问题结论,教师适当进行点评。 问题的设置意在加强棱锥和正棱锥定义的理解。
应用举例 例1:设计一个平面图形,使他能够折成一个侧面与底面都是等边三角形的正三棱锥。例2:已知正四棱锥V-ABCD(如图),底面面积为16,一条侧棱为 ,计算它的高和斜高。 学生分组共同探讨,分析解题思路。教师展示解题过程,注意规范解题步骤。 通过探索寻找正棱锥中的直角三角形,将所有量转化到同一直角三角形中解决问题,让学生体验转化的思想方法。
概念形成 1.棱台的定义2.棱台的性质(1) 上下底面平行且相似,对边平行(2) 侧面是梯形(3) 侧棱延长线交于一点3.棱台的有关概念棱台的元素棱台的表示方法棱台的分类正棱台和斜高 教师通过课件展示棱台的形成,得到棱台的定义;并引导学生通过类比棱锥的特征性质来归纳出棱台的特征性质。让学生总结结论,教师进行评判和更正。 通过课件的演示,使学生直观了解棱台的结构特点,培养学生的几何直观能力。
概念深化 辨析:下图中的几何体是不是棱台 教师提出问题,学生分组讨论。由学生探索归纳问题结论,教师适当进行点评。 问题的设置意在加强棱台定义的理解。
归纳小结 棱锥、棱柱的定义和性质棱柱、棱锥和棱台的关系将空间问题转化成平面问题的转化思想 学生小结并互相补充,师生共同整理完善。 学生反思总结,可以提高学生自己获取知识的能力以及归纳概括能力。
布置作业 必做题:教材11页练习B 3、4 题选择题:教材33页习题B 4题 必做题要求所有学生都要完成,选做题只要求学有余力的同学完成。 学生课后巩固所学知识
板书设计 棱锥和棱台图形 正棱锥的性质 例 题 小 结棱锥的性质 棱台的性质
教学目标 1.知识与能力目标 认知和了解棱锥和棱台的结构特征,掌握其定义和性质
2.过程与方法目标 培养学生的空间想象能力,并体验转化和类比的思想方法
3.情感、态度和价值观目标 通过计算机课件演示,体现一种几何体的数学直观美,激发学生的学习欲望和探究精神,并培养学生积极参与、大胆探索的精神以及合作意识
教学重点和难点 重 点 棱锥和棱台的定义及性质以及正棱锥的性质
难 点 将空间问题转化成平面问题
教学方法 问题探索式 教 具 多媒体、模型
教学环节 教学内容 师生互动 设计意图
课题引入 展示课堂教学目标让演示图片,展示生活中的一些特殊多面体,引出本节所学知识棱锥和棱台。提出本节课的教学目标。 教师演示课件,展示生活中的棱锥的实例(金字塔)。 1、学生对本节课的学习内容有一个清晰的认识,带着明确的学习目标去学习2、通过课件展示,使学生直观了解棱锥。
概念形成 1. 棱锥的定义2. 棱锥的性质(1)底面是多边形(2)侧面是有一个公共顶点的三角形3. 棱锥的有关概念(1)棱锥的元素(2)棱锥的表示方法(3)棱锥的分类(4)正棱锥和斜高 教师展示课件,并提出问题,在通过类比棱柱的有关概念,得到棱锥的结构特点。 通过简单动画的演示,使学生直观了解棱锥的结构特点,培养学生的几何直观能力。
概念深化 提出问题:1. 有一个面是多边形其余各面是三角形,这个多面体一定是棱锥吗?2.底面是多边形的棱锥一定是正棱锥吗?正棱锥的性质:(1)八个基本量:侧棱、底边、高、斜高、底面内切圆半径、底面外切圆半径、线面角、面面角(2)从正棱锥中寻找到四个面都是直角三角形的三棱锥 教师提出问题,学生分组讨论。由学生探索归纳问题结论,教师适当进行点评。 问题的设置意在加强棱锥和正棱锥定义的理解。
应用举例 例1:设计一个平面图形,使他能够折成一个侧面与底面都是等边三角形的正三棱锥。例2:已知正四棱锥V-ABCD(如图),底面面积为16,一条侧棱为 ,计算它的高和斜高。 学生分组共同探讨,分析解题思路。教师展示解题过程,注意规范解题步骤。 通过探索寻找正棱锥中的直角三角形,将所有量转化到同一直角三角形中解决问题,让学生体验转化的思想方法。
概念形成 1.棱台的定义2.棱台的性质(1) 上下底面平行且相似,对边平行(2) 侧面是梯形(3) 侧棱延长线交于一点3.棱台的有关概念棱台的元素棱台的表示方法棱台的分类正棱台和斜高 教师通过课件展示棱台的形成,得到棱台的定义;并引导学生通过类比棱锥的特征性质来归纳出棱台的特征性质。让学生总结结论,教师进行评判和更正。 通过课件的演示,使学生直观了解棱台的结构特点,培养学生的几何直观能力。
概念深化 辨析:下图中的几何体是不是棱台 教师提出问题,学生分组讨论。由学生探索归纳问题结论,教师适当进行点评。 问题的设置意在加强棱台定义的理解。
归纳小结 棱锥、棱柱的定义和性质棱柱、棱锥和棱台的关系将空间问题转化成平面问题的转化思想 学生小结并互相补充,师生共同整理完善。 学生反思总结,可以提高学生自己获取知识的能力以及归纳概括能力。
布置作业 必做题:教材11页练习B 3、4 题选择题:教材33页习题B 4题 必做题要求所有学生都要完成,选做题只要求学有余力的同学完成。 学生课后巩固所学知识
板书设计 棱锥和棱台图形 正棱锥的性质 例 题 小 结棱锥的性质 棱台的性质
