高中数学人教新课标B版必修2--几何体的外接球 专题课件(共18张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修2--几何体的外接球 专题课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 865.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 08:40:19 | ||
图片预览


文档简介
(共18张PPT)
1、球体的体积与表面积
一、知识回顾:
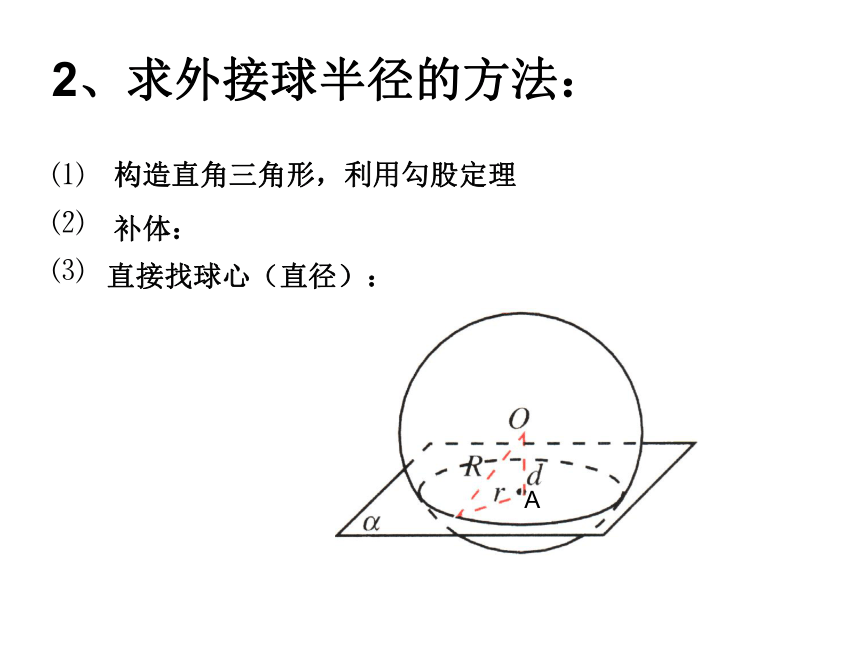
2、求外接球半径的方法:
⑴
⑵
⑶
直接找球心(直径):
补体:
构造直角三角形,利用勾股定理
A
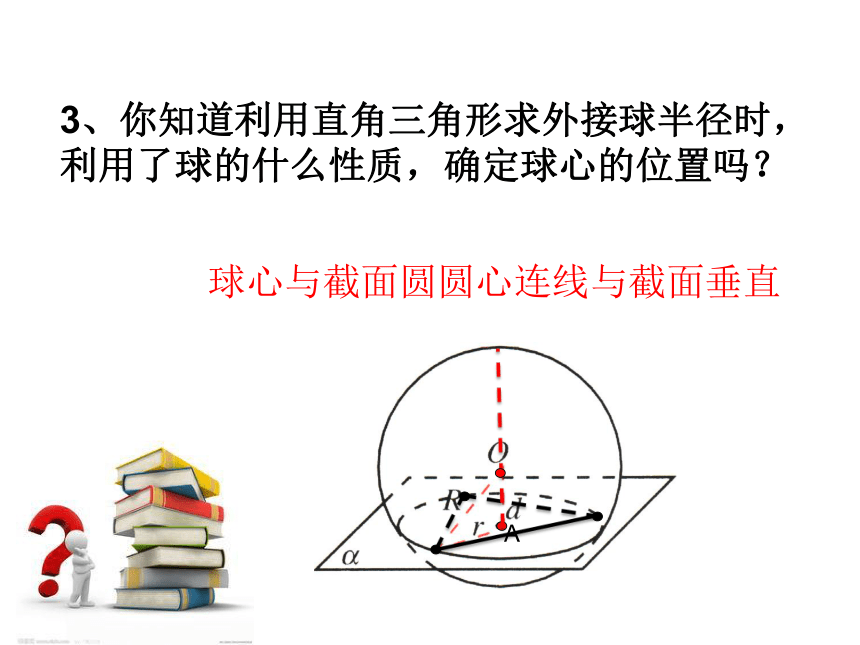
3、你知道利用直角三角形求外接球半径时,利用了球的什么性质,确定球心的位置吗?
球心与截面圆圆心连线与截面垂直
A
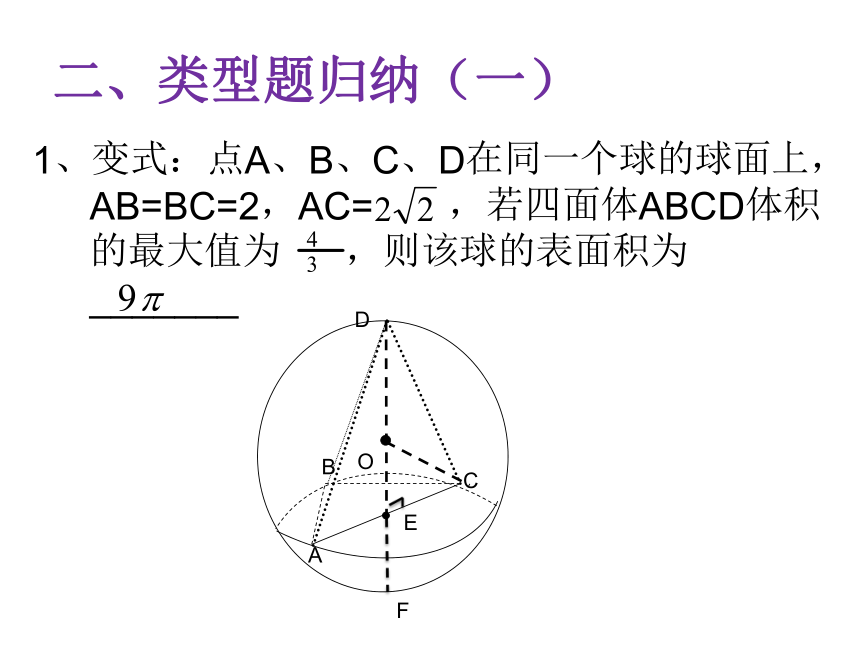
二、类型题归纳(一)
1、变式:点A、B、C、D在同一个球的球面上,AB=BC=2,AC= ,若四面体ABCD体积的最大值为 ,则该球的表面积为_______
A
B
C
E
D
O
F
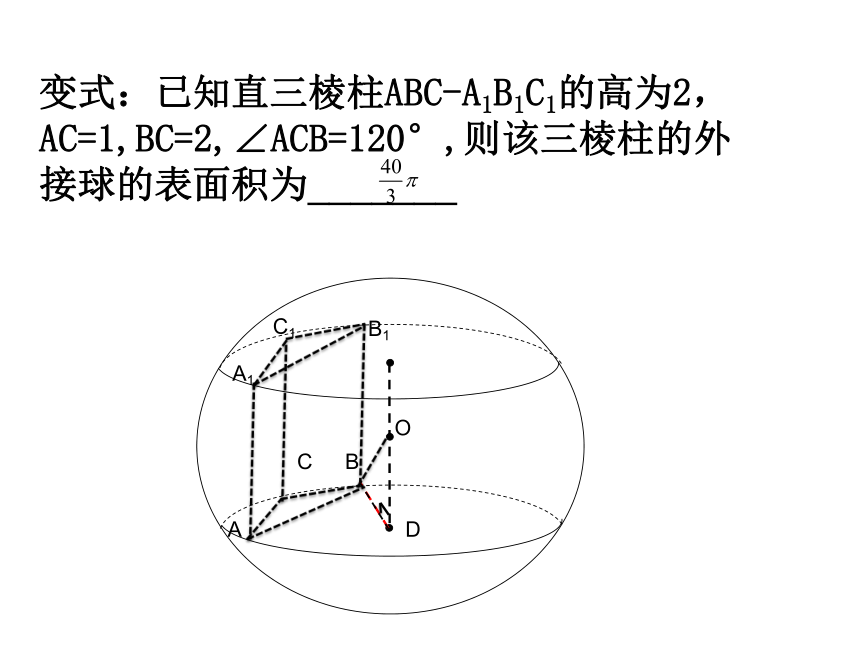
变式:已知直三棱柱ABC-A1B1C1的高为2,AC=1,BC=2,∠ACB=120°,则该三棱柱的外接球的表面积为_______
A
B1
C1
A1
B
C
O
D
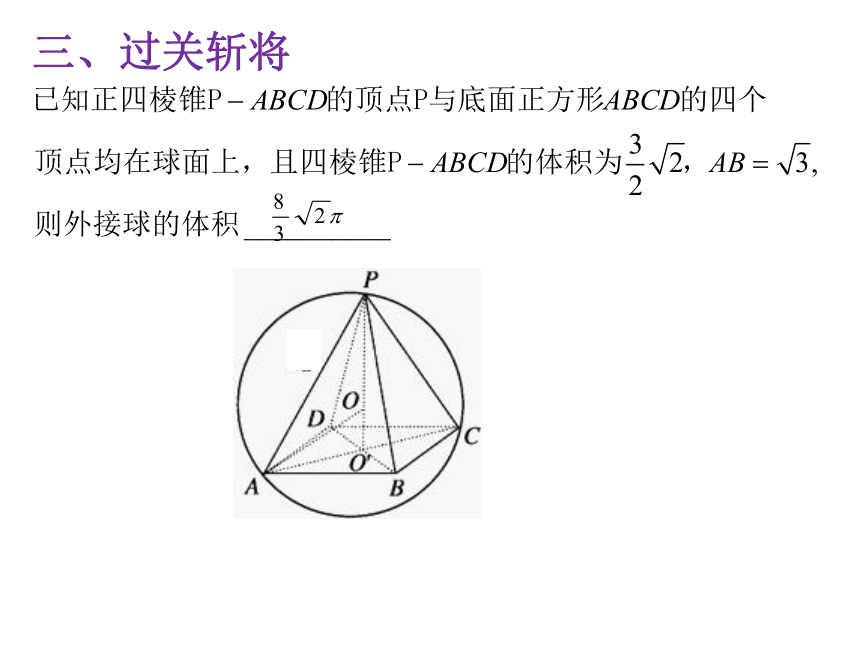
三、过关斩将
二、类型题归纳(二)
1、正三棱锥P-ABC中,PA,PB,PC两两垂直,且侧棱长为2 ,求三棱锥外接球表面积_______
P
B
A
C
A
B
C
P
变式:正三棱锥P-ABC中,M,N为PC,BC中点,且MN⊥AM,侧棱长为2 ,求三棱锥外接球表面积_______
M
A
N
B
C
P
P
B
A
C
M
N
2、三棱锥S-ABC的所有顶点都在球O的表面上,SA⊥平面ABC,AB⊥BC,又SA=AB=BC=1,则球O的表面积为_______
B
A
C
S
2、三棱锥S-ABC的所有顶点都在球O的表面上,SA⊥平面ABC,AB⊥BC,又SA=AB=BC=1,则球O的表面积为_______
B
A
C
S
A
C
S
B
2、三棱锥S-ABC的所有顶点都在球O的表面上,SA⊥平面ABC,AB⊥BC,又SA=AB=BC=1,则球O的表面积为_______
B
A
C
S
S
A
B
C
2、三棱锥S-ABC的所有顶点都在球O的表面上,SA⊥平面ABC,又SA=2,AB=BC=AC=1,则球O的表面积为_______
B
A
C
S
A
C
S
B
三、过关斩将
变式2:已知一个四面体的每个面都是有两条边长为3,一条边长为2的三角形,则该四面体的外接球的表面积_______
D
B
A
C
A
B
C
D
3
3
2
2
3
3
1、正三角形ABC的边长为2,将它沿高AD翻折,使点B与点C间的距离为1,此时四面体ABCD外接球表面积为_______
A
C
B
D
A
B
D
C
四、挑战提升
2、已知三角形PAD所在平面与矩形ABCD所在平面互相垂直,PA=AB=PD=2,∠APD=120°,则四棱锥P-ABCD的外接球表面积为_______
A
D
P
B
C
6、矩形ABCD,AB=4,BC=3,沿AC将ABC折起使平面ABC⊥平面ACD,求四面体A-BCD的外接球体积__________
变式1:矩形ABCD,AB=4,BC=3,沿AC将ABC折起成一个二面角B-AC-D,求四面体A-BCD的外接球体积__________
图3
四、课堂小结
本堂课你有什么收获:
1、球体的体积与表面积
一、知识回顾:
2、求外接球半径的方法:
⑴
⑵
⑶
直接找球心(直径):
补体:
构造直角三角形,利用勾股定理
A
3、你知道利用直角三角形求外接球半径时,利用了球的什么性质,确定球心的位置吗?
球心与截面圆圆心连线与截面垂直
A
二、类型题归纳(一)
1、变式:点A、B、C、D在同一个球的球面上,AB=BC=2,AC= ,若四面体ABCD体积的最大值为 ,则该球的表面积为_______
A
B
C
E
D
O
F
变式:已知直三棱柱ABC-A1B1C1的高为2,AC=1,BC=2,∠ACB=120°,则该三棱柱的外接球的表面积为_______
A
B1
C1
A1
B
C
O
D
三、过关斩将
二、类型题归纳(二)
1、正三棱锥P-ABC中,PA,PB,PC两两垂直,且侧棱长为2 ,求三棱锥外接球表面积_______
P
B
A
C
A
B
C
P
变式:正三棱锥P-ABC中,M,N为PC,BC中点,且MN⊥AM,侧棱长为2 ,求三棱锥外接球表面积_______
M
A
N
B
C
P
P
B
A
C
M
N
2、三棱锥S-ABC的所有顶点都在球O的表面上,SA⊥平面ABC,AB⊥BC,又SA=AB=BC=1,则球O的表面积为_______
B
A
C
S
2、三棱锥S-ABC的所有顶点都在球O的表面上,SA⊥平面ABC,AB⊥BC,又SA=AB=BC=1,则球O的表面积为_______
B
A
C
S
A
C
S
B
2、三棱锥S-ABC的所有顶点都在球O的表面上,SA⊥平面ABC,AB⊥BC,又SA=AB=BC=1,则球O的表面积为_______
B
A
C
S
S
A
B
C
2、三棱锥S-ABC的所有顶点都在球O的表面上,SA⊥平面ABC,又SA=2,AB=BC=AC=1,则球O的表面积为_______
B
A
C
S
A
C
S
B
三、过关斩将
变式2:已知一个四面体的每个面都是有两条边长为3,一条边长为2的三角形,则该四面体的外接球的表面积_______
D
B
A
C
A
B
C
D
3
3
2
2
3
3
1、正三角形ABC的边长为2,将它沿高AD翻折,使点B与点C间的距离为1,此时四面体ABCD外接球表面积为_______
A
C
B
D
A
B
D
C
四、挑战提升
2、已知三角形PAD所在平面与矩形ABCD所在平面互相垂直,PA=AB=PD=2,∠APD=120°,则四棱锥P-ABCD的外接球表面积为_______
A
D
P
B
C
6、矩形ABCD,AB=4,BC=3,沿AC将ABC折起使平面ABC⊥平面ACD,求四面体A-BCD的外接球体积__________
变式1:矩形ABCD,AB=4,BC=3,沿AC将ABC折起成一个二面角B-AC-D,求四面体A-BCD的外接球体积__________
图3
四、课堂小结
本堂课你有什么收获:
