高中数学人教新课标B版必修2《1.1.7 柱、锥、台和球的体积》 课件(共34张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修2《1.1.7 柱、锥、台和球的体积》 课件(共34张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 627.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 00:00:00 | ||
图片预览



文档简介
(共34张PPT)
1.1.7 柱、锥、台和球的体积
复习回顾
1.正方体的体积公式
V正方体=a3(这里a为棱长)
2.长方体的体积公式
V长方体=abc(这里a,b,c分别为长方体长、宽、高)
或V长方体=sh(s,h分别表示长方体的底面积和高)
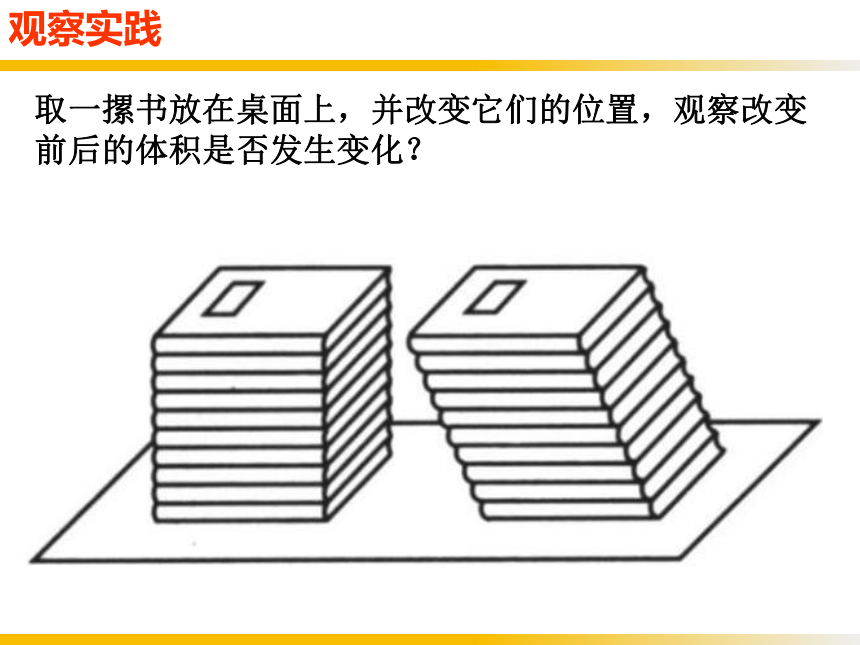
观察实践
取一摞书放在桌面上,并改变它们的位置,观察改变前后的体积是否发生变化?
祖暅原理:幂势既同,则积不容异。
夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等。
等底面积、等高的两个柱体或锥体的体积相等。
我国古代对几何体的体积研究,取得了光辉的成就,并建立了完整的理论体系。
祖暅是我国古代南北朝时期(5世纪)的数学家,他在总结前人研究的基础上,总 结出这个原理,在欧洲直到17世纪,才由意大利的卡瓦列里提出这个事实。
S
S
h
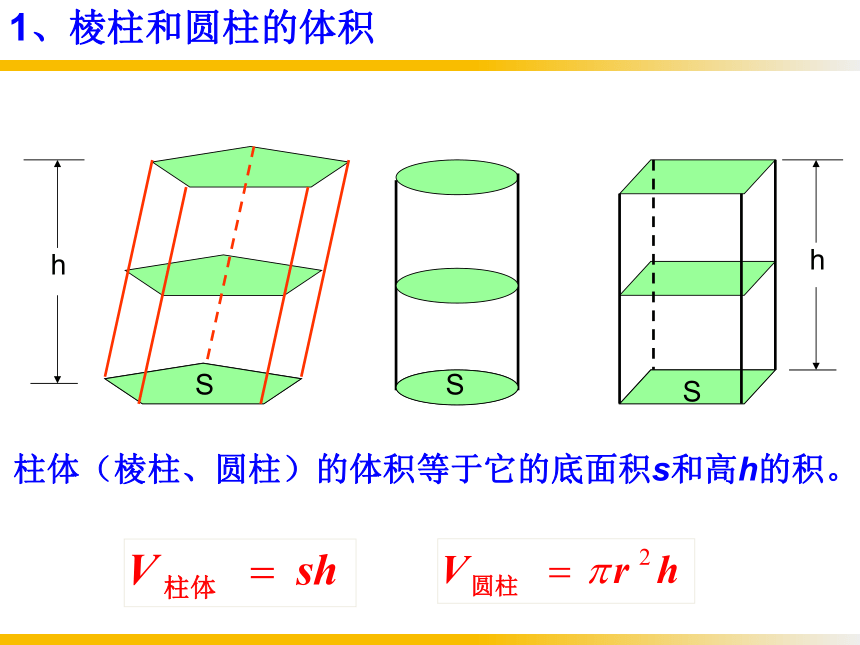
1、棱柱和圆柱的体积
S
h
柱体(棱柱、圆柱)的体积等于它的底面积s和高h的积。
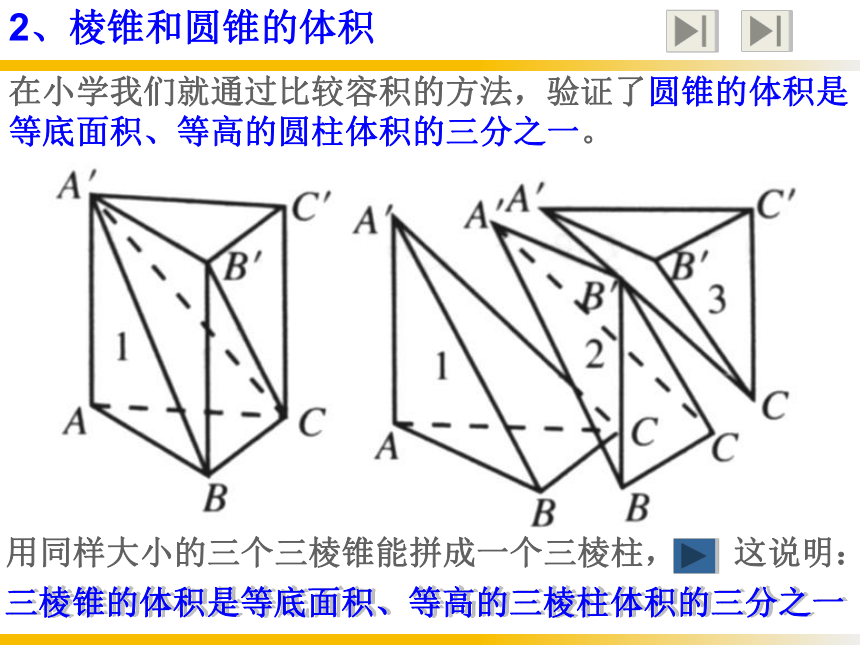
2、棱锥和圆锥的体积
在小学我们就通过比较容积的方法,验证了圆锥的体积是等底面积、等高的圆柱体积的三分之一。
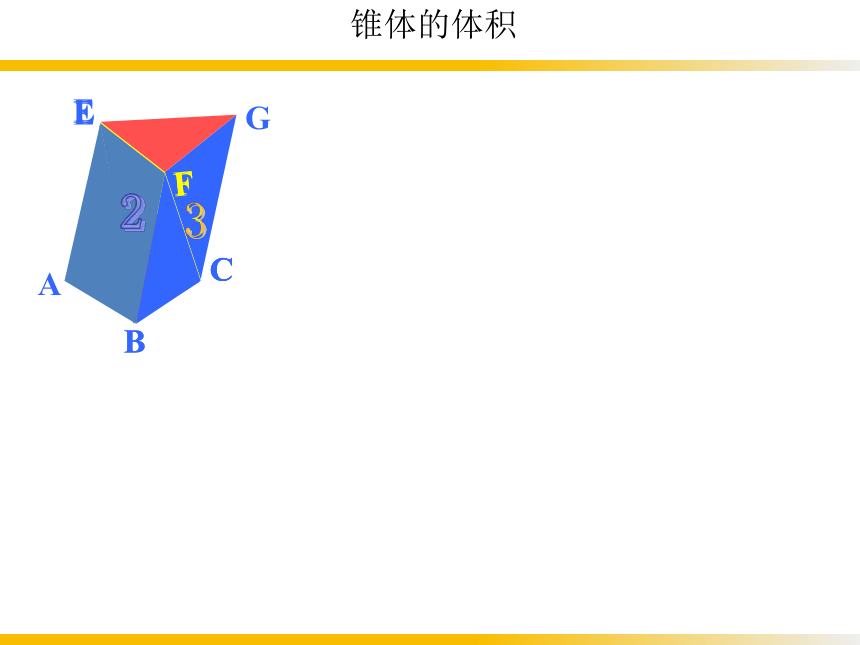
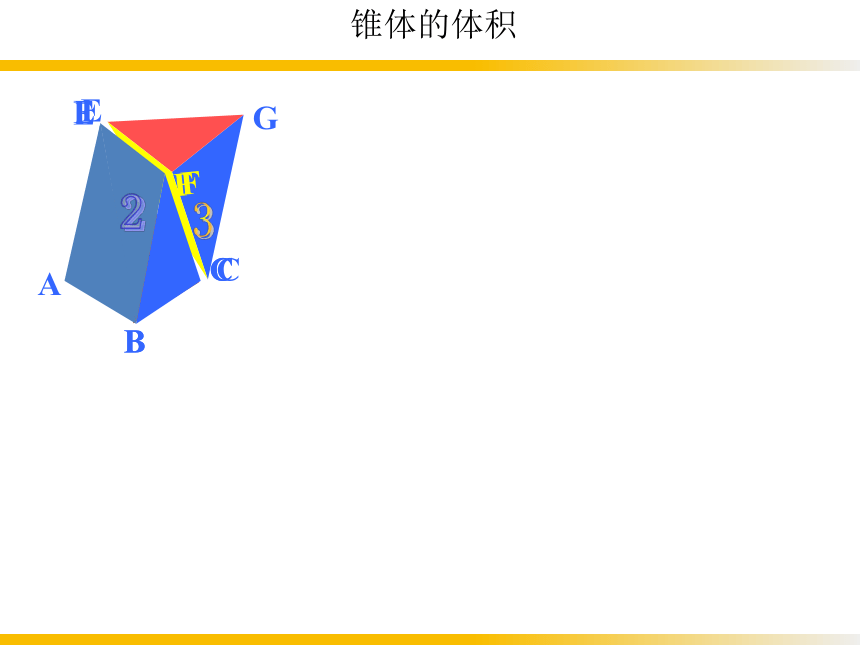
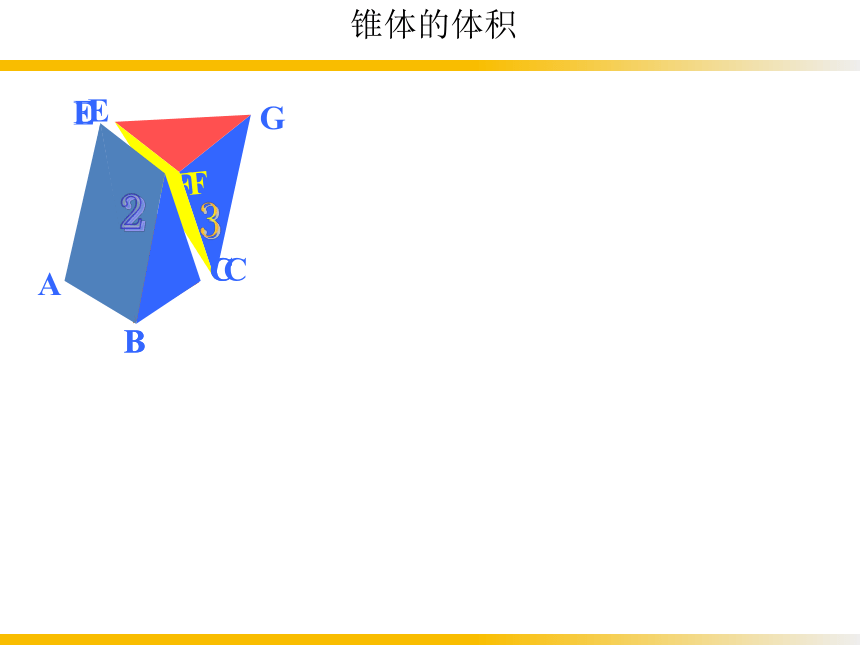
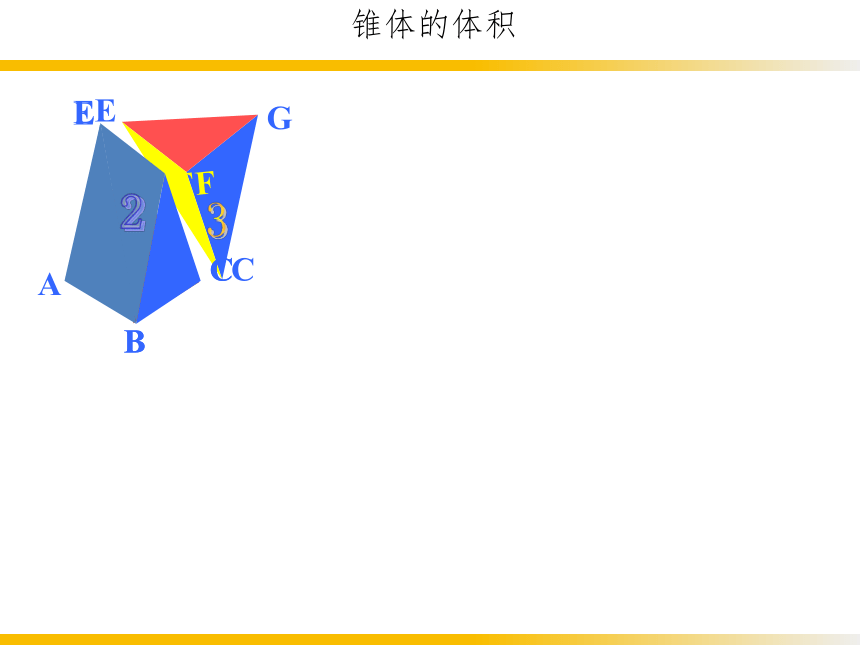
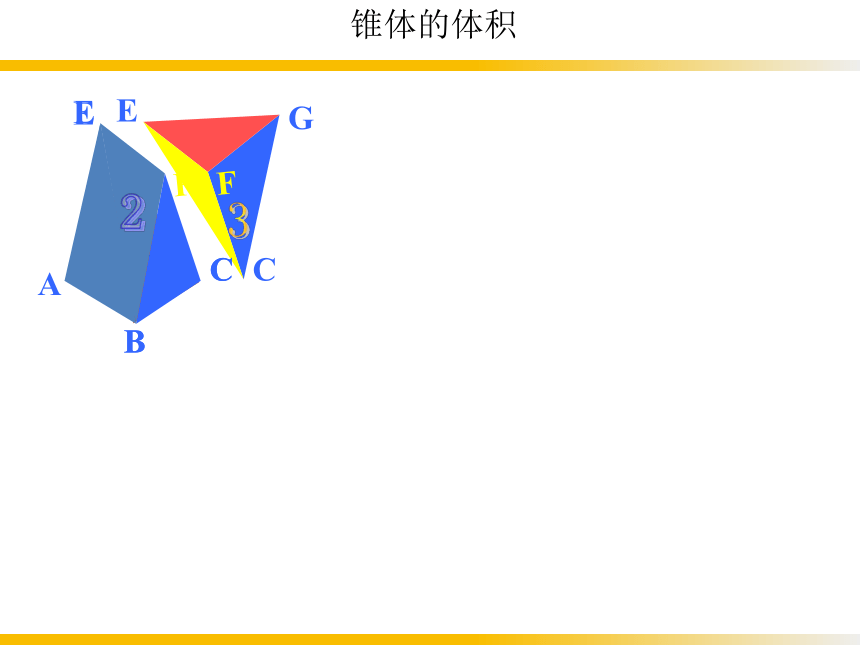
用同样大小的三个三棱锥能拼成一个三棱柱, 这说明:
三棱锥的体积是等底面积、等高的三棱柱体积的三分之一
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
B
E
C
A
C
F
B
E
锥体的体积
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
由祖暅原理和以上基础,可以推出:底面积相等,高也相等的两个锥体的体积也相等.
S为底面积,h为高.
s
s
2、棱锥和圆锥的体积
h
h
s
s/
s
s/
h
x
若台体的上下底面积分别是s/,s,高是h,则
3、棱台和圆台的体积
台体的体积可以用两个锥体的体积的差来计算。
V台体=
V柱体=sh
V锥体=
s
s/
s
s/
s
S/=0
S=S’
柱体、锥体、台体的体积公式之间有什么关系呢?
V球=
4、球的体积
B
C
A
D
应用举例
A
D
应用举例
B
C
例2:如图 有一堆相同规格的六角螺帽毛坯共重5.8kg.已知底面正六边形的边长是12mm,高是10mm,内孔直径是10mm.那么约有毛坯多少个?(铁的密度是7.8g/cm3).
分析:六角螺帽毛坯的体积是一个正六棱柱的体积与一个圆柱的体积的差,再由密度算出一个六角螺帽毛坯的质量即可.
答:这堆螺帽约有250个。
应用举例
教材P32-1.1.7练习A
巩固练习
D1
A1
B1
C1
C
B
D
A
A
B1
C
D1
D1
B1
C
A
D1
B1
C
A
柱体
锥体
台体
球
课堂小结
1.1.7 柱、锥、台和球的体积
复习回顾
1.正方体的体积公式
V正方体=a3(这里a为棱长)
2.长方体的体积公式
V长方体=abc(这里a,b,c分别为长方体长、宽、高)
或V长方体=sh(s,h分别表示长方体的底面积和高)
观察实践
取一摞书放在桌面上,并改变它们的位置,观察改变前后的体积是否发生变化?
祖暅原理:幂势既同,则积不容异。
夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等。
等底面积、等高的两个柱体或锥体的体积相等。
我国古代对几何体的体积研究,取得了光辉的成就,并建立了完整的理论体系。
祖暅是我国古代南北朝时期(5世纪)的数学家,他在总结前人研究的基础上,总 结出这个原理,在欧洲直到17世纪,才由意大利的卡瓦列里提出这个事实。
S
S
h
1、棱柱和圆柱的体积
S
h
柱体(棱柱、圆柱)的体积等于它的底面积s和高h的积。
2、棱锥和圆锥的体积
在小学我们就通过比较容积的方法,验证了圆锥的体积是等底面积、等高的圆柱体积的三分之一。
用同样大小的三个三棱锥能拼成一个三棱柱, 这说明:
三棱锥的体积是等底面积、等高的三棱柱体积的三分之一
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
B
E
C
A
C
F
B
E
锥体的体积
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
C
E
G
F
锥体的体积
B
E
C
A
C
F
B
E
由祖暅原理和以上基础,可以推出:底面积相等,高也相等的两个锥体的体积也相等.
S为底面积,h为高.
s
s
2、棱锥和圆锥的体积
h
h
s
s/
s
s/
h
x
若台体的上下底面积分别是s/,s,高是h,则
3、棱台和圆台的体积
台体的体积可以用两个锥体的体积的差来计算。
V台体=
V柱体=sh
V锥体=
s
s/
s
s/
s
S/=0
S=S’
柱体、锥体、台体的体积公式之间有什么关系呢?
V球=
4、球的体积
B
C
A
D
应用举例
A
D
应用举例
B
C
例2:如图 有一堆相同规格的六角螺帽毛坯共重5.8kg.已知底面正六边形的边长是12mm,高是10mm,内孔直径是10mm.那么约有毛坯多少个?(铁的密度是7.8g/cm3).
分析:六角螺帽毛坯的体积是一个正六棱柱的体积与一个圆柱的体积的差,再由密度算出一个六角螺帽毛坯的质量即可.
答:这堆螺帽约有250个。
应用举例
教材P32-1.1.7练习A
巩固练习
D1
A1
B1
C1
C
B
D
A
A
B1
C
D1
D1
B1
C
A
D1
B1
C
A
柱体
锥体
台体
球
课堂小结
