高中数学人教新课标B版必修2--《1.2.3 空间中的垂直关系》 课件(共18张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修2--《1.2.3 空间中的垂直关系》 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 566.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 08:42:52 | ||
图片预览





文档简介
(共18张PPT)
空间中的垂直关系
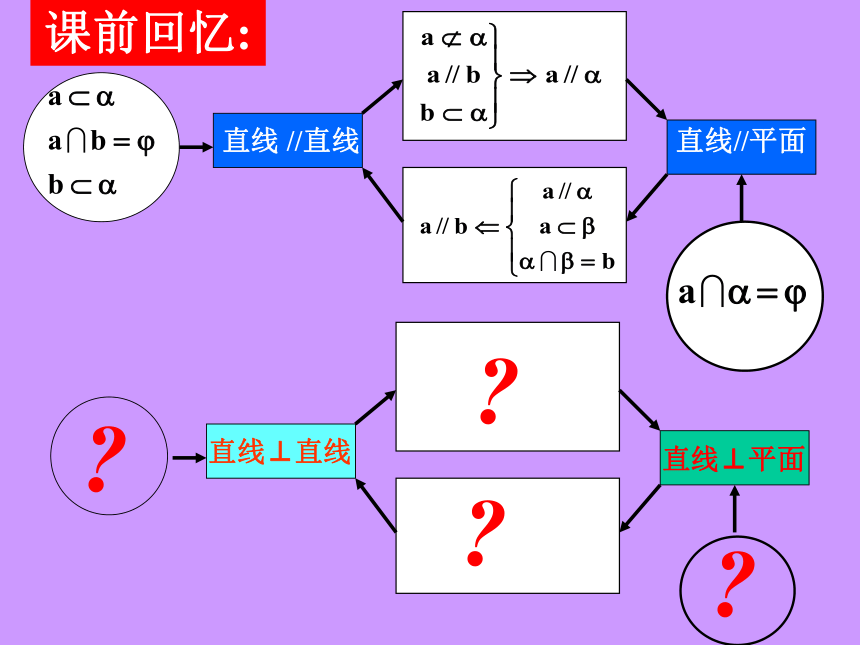
课前回忆:
直线 //直线
直线//平面
直线⊥直线
直线⊥平面
如果两条直线相交一点或经过平移后相交于一点,并且交角为直角(90°),则称这两条直线互相垂直.
两条直线垂直,有相交一点的垂直;
(2) 两条直线垂直还可以异面直线垂直;
(就是不相交的垂直)
一.直线与直线垂直定义
1. 直线垂直平面的定义:
如果直线( AB)和一个平面(α)相交于点O, 并且和这个平面内过点(O)的任何直线都垂直,那么就说这条直线和这个平面垂直。
α
O
L
二.直线垂直平面
记作: L ⊥α。
直线 L 叫做平面α的垂线。
平面α叫做直线 L 的垂面。
直线 L 和平面α的交点P叫做垂足。
α
P
L
直线垂直平面的术语:
二、填空题:
2、直线和平面垂直的判定定理
如果一条直线和一个平面内的
两条相交直线都垂直,那么这条直线垂直于这个平面。
L
m α
n α
m ∩ n = B
l ⊥ m
l ⊥ n
l ⊥α
n
m
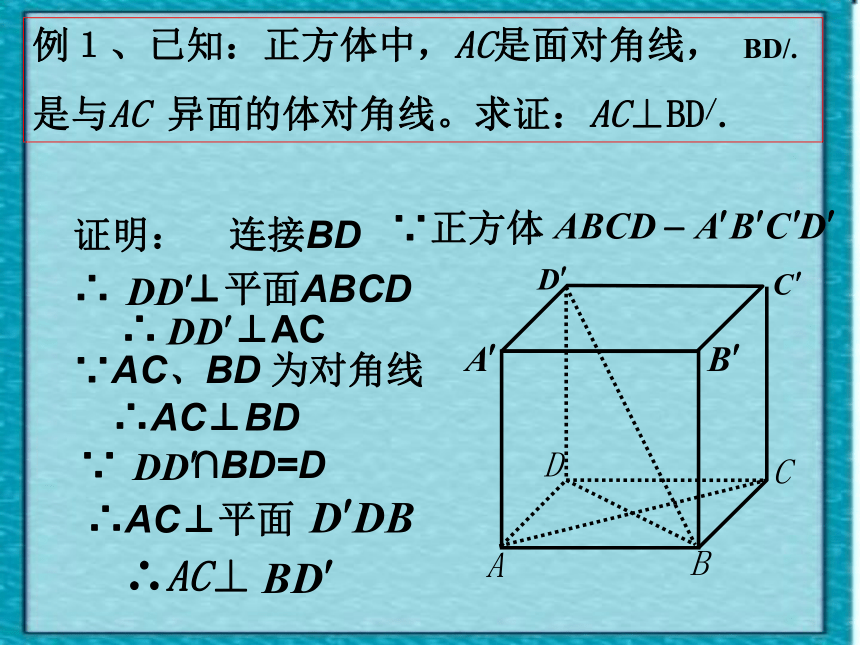
证明:
连接BD
∵AC、BD 为对角线
∴AC⊥BD
例1、已知:正方体中,AC是面对角线, BD/.
是与AC 异面的体对角线。求证:AC⊥BD/.
∴ ⊥平面ABCD
∵正方体
A
B
D
C
∴ ⊥AC
∵ ∩BD=D
∴AC⊥平面
∴AC⊥
(1)如果三条直线共点、且两两垂直,其中任一条直线是否垂直于另两条直线确定的平面?为什么?
练习1、
(2)如果一条直线垂直于一个三角形的两边,能否断定这条直线和三角形的第三条边垂直?为什么?
(1)垂直!先证一条直线垂直另两条(相交)。
(2)能垂直!先证一条直线垂直 三角形平面。
(3)判断下列命题的真假:
①若a⊥m,a⊥n,m α,n α,则a⊥α。
②若a⊥α,b α,则a⊥b。
③若a⊥α,a⊥b,则b//α。
④线段AB的垂直平分面内任意一点到A、B的
距离均相等。
⑤若a垂直于平面α内的无数条直线,则a⊥α。
⑥若a⊥α于A,AB⊥a,则AB α。
⑦若a//α,b⊥a,则b⊥α。
如果一条直线垂直于一个平面,
那么它就和平面内任何一条直线都垂直。
3、直线与平面垂直的性质
格式:
例题2、如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于同一个平面。
a
b
已知:a , a‖b.
求证:b .
m
证明:
设m是 内的任意一条直线。
a
m
b
a‖b
a m
m
b m
直线与平面垂直的性质
直线与平面垂直的性质
练习2、如果两条直线垂直于同一个平面,
那么这两条直线互相平行。
a
b
a‖b
a
b
C
o
例题3、设 是任意平面,点p是空间任一点。则:
过p有且只有一条直线 与 垂直。
从平面外一点引这个平面的垂线,这个点和垂足间的距离叫做这个点到这个平面的距离。
α
P
l
P
常用结论(1)
设 是任一直线,点p是空间任一点。
则:
过点p有且只有一个平面 垂直 。
α
P
l
P
常用结论(2)
练习3、如果一条直线a在投射面上的正投 影 a/垂直于投射面上的一条直线 b,那么这条直线 a和投射面上直线 b垂直。
a
a/
b
例题4、 有一根旗杆AB 高 8m,它的顶点 A挂着两条长10m的绳子,拉紧绳子,并把它的下端放在地面上的两点 C , D ( 和旗杆脚不在同一直线上),如果这两点都和旗脚 B的距离是 6m,那么旗杆为什么和地面是垂直的 ( 课本P50-例题2)
α
A
D
C
B
练习4、四棱锥P-ABCD 的底面是矩形,
PA⊥平面 AC, 且有AD=2, AB= ,
确定点M在线段 BC上
什么位置时PM ⊥MD。
P
A
B
M
C
D
答:点M距离点B为
直线⊥直线 <===>直线⊥平面
线//线
线//面
面//面
线⊥线
线⊥面
面⊥面
空间中的垂直关系
课前回忆:
直线 //直线
直线//平面
直线⊥直线
直线⊥平面
如果两条直线相交一点或经过平移后相交于一点,并且交角为直角(90°),则称这两条直线互相垂直.
两条直线垂直,有相交一点的垂直;
(2) 两条直线垂直还可以异面直线垂直;
(就是不相交的垂直)
一.直线与直线垂直定义
1. 直线垂直平面的定义:
如果直线( AB)和一个平面(α)相交于点O, 并且和这个平面内过点(O)的任何直线都垂直,那么就说这条直线和这个平面垂直。
α
O
L
二.直线垂直平面
记作: L ⊥α。
直线 L 叫做平面α的垂线。
平面α叫做直线 L 的垂面。
直线 L 和平面α的交点P叫做垂足。
α
P
L
直线垂直平面的术语:
二、填空题:
2、直线和平面垂直的判定定理
如果一条直线和一个平面内的
两条相交直线都垂直,那么这条直线垂直于这个平面。
L
m α
n α
m ∩ n = B
l ⊥ m
l ⊥ n
l ⊥α
n
m
证明:
连接BD
∵AC、BD 为对角线
∴AC⊥BD
例1、已知:正方体中,AC是面对角线, BD/.
是与AC 异面的体对角线。求证:AC⊥BD/.
∴ ⊥平面ABCD
∵正方体
A
B
D
C
∴ ⊥AC
∵ ∩BD=D
∴AC⊥平面
∴AC⊥
(1)如果三条直线共点、且两两垂直,其中任一条直线是否垂直于另两条直线确定的平面?为什么?
练习1、
(2)如果一条直线垂直于一个三角形的两边,能否断定这条直线和三角形的第三条边垂直?为什么?
(1)垂直!先证一条直线垂直另两条(相交)。
(2)能垂直!先证一条直线垂直 三角形平面。
(3)判断下列命题的真假:
①若a⊥m,a⊥n,m α,n α,则a⊥α。
②若a⊥α,b α,则a⊥b。
③若a⊥α,a⊥b,则b//α。
④线段AB的垂直平分面内任意一点到A、B的
距离均相等。
⑤若a垂直于平面α内的无数条直线,则a⊥α。
⑥若a⊥α于A,AB⊥a,则AB α。
⑦若a//α,b⊥a,则b⊥α。
如果一条直线垂直于一个平面,
那么它就和平面内任何一条直线都垂直。
3、直线与平面垂直的性质
格式:
例题2、如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于同一个平面。
a
b
已知:a , a‖b.
求证:b .
m
证明:
设m是 内的任意一条直线。
a
m
b
a‖b
a m
m
b m
直线与平面垂直的性质
直线与平面垂直的性质
练习2、如果两条直线垂直于同一个平面,
那么这两条直线互相平行。
a
b
a‖b
a
b
C
o
例题3、设 是任意平面,点p是空间任一点。则:
过p有且只有一条直线 与 垂直。
从平面外一点引这个平面的垂线,这个点和垂足间的距离叫做这个点到这个平面的距离。
α
P
l
P
常用结论(1)
设 是任一直线,点p是空间任一点。
则:
过点p有且只有一个平面 垂直 。
α
P
l
P
常用结论(2)
练习3、如果一条直线a在投射面上的正投 影 a/垂直于投射面上的一条直线 b,那么这条直线 a和投射面上直线 b垂直。
a
a/
b
例题4、 有一根旗杆AB 高 8m,它的顶点 A挂着两条长10m的绳子,拉紧绳子,并把它的下端放在地面上的两点 C , D ( 和旗杆脚不在同一直线上),如果这两点都和旗脚 B的距离是 6m,那么旗杆为什么和地面是垂直的 ( 课本P50-例题2)
α
A
D
C
B
练习4、四棱锥P-ABCD 的底面是矩形,
PA⊥平面 AC, 且有AD=2, AB= ,
确定点M在线段 BC上
什么位置时PM ⊥MD。
P
A
B
M
C
D
答:点M距离点B为
直线⊥直线 <===>直线⊥平面
线//线
线//面
面//面
线⊥线
线⊥面
面⊥面
