高中数学人教新课标B版必修2--《2.3.4 圆与圆的位置关系》 课件(共19张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修2--《2.3.4 圆与圆的位置关系》 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 469.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 08:48:04 | ||
图片预览




文档简介
(共19张PPT)
2.3.4 圆与圆的位置关系
人教B版必修二
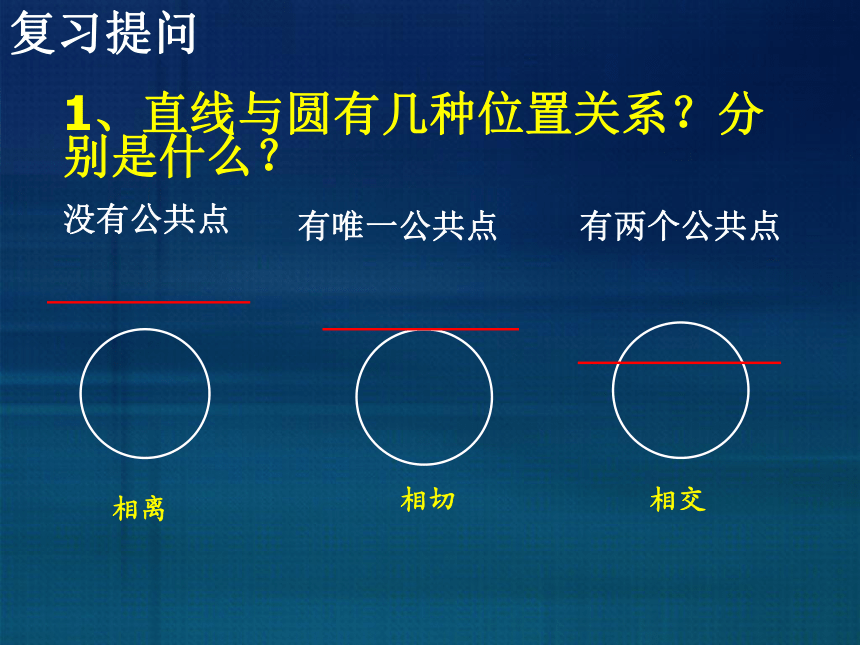
相交
相离
相切
没有公共点
有唯一公共点
有两个公共点
复习提问
1、直线与圆有几种位置关系?分别是什么?
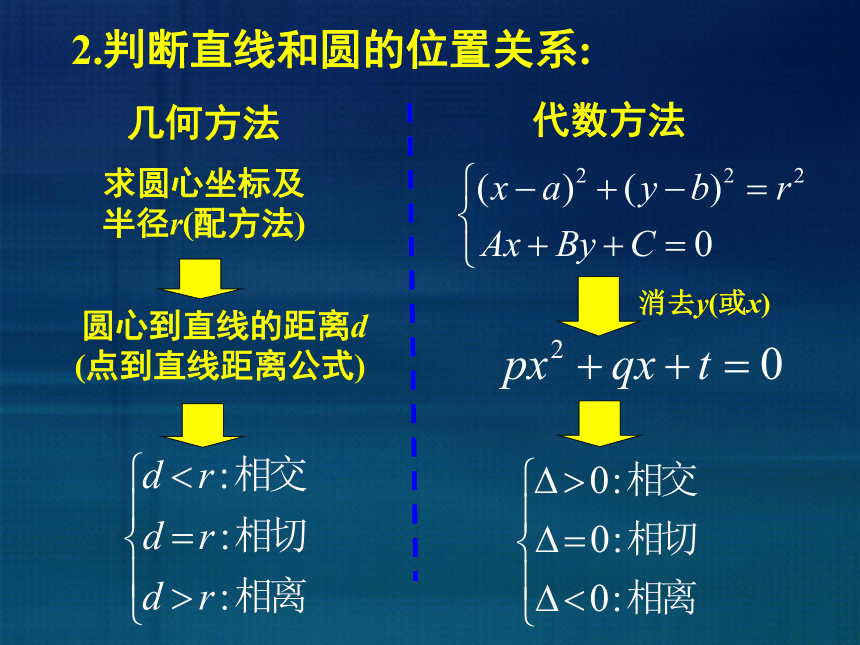
2.判断直线和圆的位置关系:
几何方法
求圆心坐标及
半径r(配方法)
圆心到直线的距离d
(点到直线距离公式)
代数方法
消去y(或x)
如果把这里的直线改为圆,则圆与圆之间又会有什么样的位置关系呢?我们又如何判断这些位置关系。
·
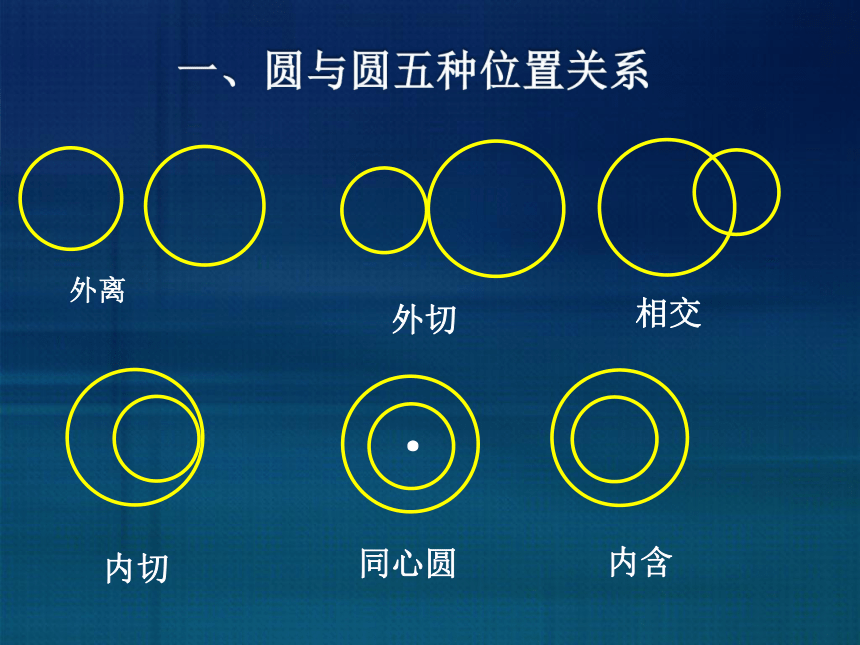
外离
外切
相交
内切
内含
同心圆
根据交点个数对圆与圆位置关系进行分类
1、没有交点
2、有一个公共点
3、有两个公共点
外离和内含
内切和外切
相交
相离
相切
相交
自我小测
1、如果两圆无公共点,那么这两个圆外离。
2、两个半径不相等的同心圆从位置关系上来说是内含。
3若两圆有且只有一个公共点,则两圆外切。
错误
正确
错误
二、判断圆与圆的位置关系
(1)外离
(2)内含
(3)外切
(4)内切
(5)相交
思考:影响圆与圆的位置关系的数量因素是什么?
两圆的半径与圆心距之间的大小。
探究:如果设圆1半径为r1,圆2半径为r2,两个圆圆心距为d。则在五种情况下三者之间有什么样的数量关系呢?
(1)外离
(2)内含
(3)外切
(4)内切
(5)相交
练一练
8或2
3、已知⊙1和⊙2的半径分别为5cm和3cm,如果⊙1和⊙2相切,则圆心距为多少?
1、已知⊙1和⊙2的半径分别为4cm和7cm,如果圆心距为8cm,则两圆的位置关系是什么?
相交
2、已知⊙1和⊙2的半径分别为4cm和7cm,如果圆心距为18cm,则两圆的位置关系是什么?
外离
合作探究
例1 判断下列两个圆的位置关系
几何方法
两圆心坐标及半径
(配方法)
圆心距d
(两点间距离公式)
比较d和r1,r2的
大小,下结论
二、圆与圆的位置关系的判定:
合作探究:
思考:
能否用其它方法判断这两个圆的位置关系
联立方程组求解的个数
二、圆与圆的位置关系的判定:
代数方法
消去y(或x)
几何方法
两圆心坐标及半径
(配方法)
圆心距d
(两点间距离公式)
比较d和r1,r2的
大小,下结论
二、圆与圆的位置关系的判定:
代数方法
消去y(或x)
2、
内切
3、
1、判断一下两个圆的位置关系
课 堂 小 结
通过本节课的学习你学到了什么?
2、课后思考
提示:两圆相切,切点必在两圆的圆心连线上。
作业:
1、书第103页,练习A第一题
2.3.4 圆与圆的位置关系
人教B版必修二
相交
相离
相切
没有公共点
有唯一公共点
有两个公共点
复习提问
1、直线与圆有几种位置关系?分别是什么?
2.判断直线和圆的位置关系:
几何方法
求圆心坐标及
半径r(配方法)
圆心到直线的距离d
(点到直线距离公式)
代数方法
消去y(或x)
如果把这里的直线改为圆,则圆与圆之间又会有什么样的位置关系呢?我们又如何判断这些位置关系。
·
外离
外切
相交
内切
内含
同心圆
根据交点个数对圆与圆位置关系进行分类
1、没有交点
2、有一个公共点
3、有两个公共点
外离和内含
内切和外切
相交
相离
相切
相交
自我小测
1、如果两圆无公共点,那么这两个圆外离。
2、两个半径不相等的同心圆从位置关系上来说是内含。
3若两圆有且只有一个公共点,则两圆外切。
错误
正确
错误
二、判断圆与圆的位置关系
(1)外离
(2)内含
(3)外切
(4)内切
(5)相交
思考:影响圆与圆的位置关系的数量因素是什么?
两圆的半径与圆心距之间的大小。
探究:如果设圆1半径为r1,圆2半径为r2,两个圆圆心距为d。则在五种情况下三者之间有什么样的数量关系呢?
(1)外离
(2)内含
(3)外切
(4)内切
(5)相交
练一练
8或2
3、已知⊙1和⊙2的半径分别为5cm和3cm,如果⊙1和⊙2相切,则圆心距为多少?
1、已知⊙1和⊙2的半径分别为4cm和7cm,如果圆心距为8cm,则两圆的位置关系是什么?
相交
2、已知⊙1和⊙2的半径分别为4cm和7cm,如果圆心距为18cm,则两圆的位置关系是什么?
外离
合作探究
例1 判断下列两个圆的位置关系
几何方法
两圆心坐标及半径
(配方法)
圆心距d
(两点间距离公式)
比较d和r1,r2的
大小,下结论
二、圆与圆的位置关系的判定:
合作探究:
思考:
能否用其它方法判断这两个圆的位置关系
联立方程组求解的个数
二、圆与圆的位置关系的判定:
代数方法
消去y(或x)
几何方法
两圆心坐标及半径
(配方法)
圆心距d
(两点间距离公式)
比较d和r1,r2的
大小,下结论
二、圆与圆的位置关系的判定:
代数方法
消去y(或x)
2、
内切
3、
1、判断一下两个圆的位置关系
课 堂 小 结
通过本节课的学习你学到了什么?
2、课后思考
提示:两圆相切,切点必在两圆的圆心连线上。
作业:
1、书第103页,练习A第一题
