高中数学人教新课标B版必修2--《1.1.2 棱柱、棱锥和棱台的结构特征》 课件(共19张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修2--《1.1.2 棱柱、棱锥和棱台的结构特征》 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 668.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 09:04:24 | ||
图片预览






文档简介
(共19张PPT)
棱柱、棱锥和棱台
的结构特征
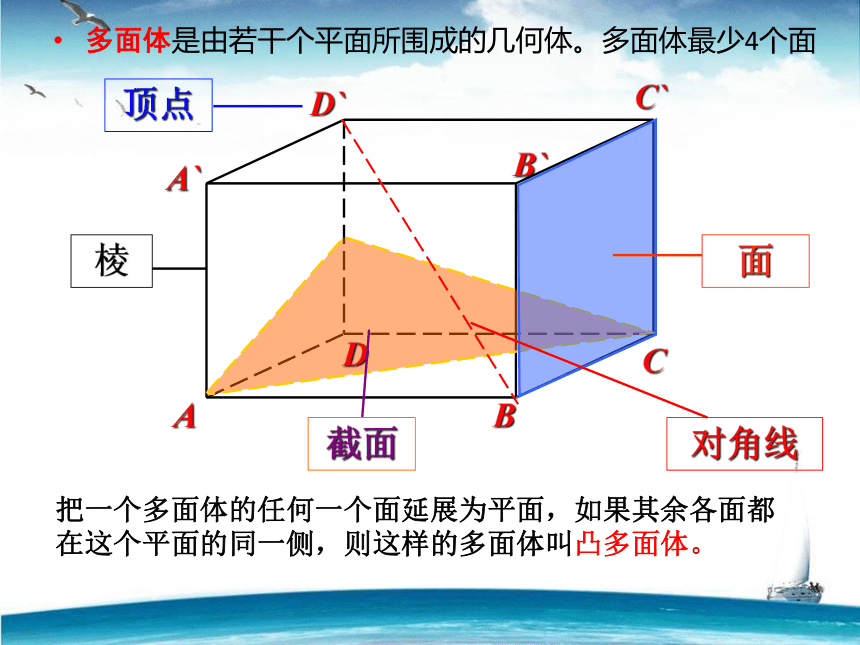
多面体是由若干个平面所围成的几何体。多面体最少4个面
A
B
C
D
A`
B`
C`
D`
棱
面
截面
顶点
对角线
把一个多面体的任何一个面延展为平面,如果其余各面都
在这个平面的同一侧,则这样的多面体叫凸多面体。
判断下列几何体哪些是多面体?
A
B
C
D
A`
B`
C`
D`
底
面
侧
面
侧
棱
高
棱柱可以看成一个多边形(包括图形围成的平面部分)上各点都沿着同一个方向移动相同的距离所形成的几何体。
棱柱的性质
自主探究1、棱柱上下两个底面关系如何,侧棱之间关系 如何?
性质1:棱柱上下两个底面互相平行,侧棱互相平行。
自主探究2、棱柱上、下两个底面的形状大小如何?各侧 面的形状如何?
性质2、棱柱上下两个底面全等,各侧面都是平行四边形。
例1
1、下列命题中,正确的是( )
A.有两个面互相平行,其余各面都是四边形的几何体叫棱柱
B.棱柱中互相平行的两个面叫做棱柱的底面
C.棱柱的侧面是平行四边形,而底面不是平行四边形
D.棱柱的侧棱都相等,侧面是平行四边形
棱柱的分类
按底面多边形分类:
底面是三角形、四边形、五边形......分别叫做三棱柱、四棱柱、五棱柱......
按侧棱与底面关系分类:
侧棱与底面垂直的棱柱叫做直棱柱。
侧棱与底面不垂直的棱柱叫做斜棱柱。
特殊棱柱
底面是正多边形的直棱柱叫做正棱柱。
底面是平行四边形的棱柱叫平行六面体。
练习
1、侧棱不垂直于底面且底面为三角形的棱柱叫做___________;
2、侧棱垂直于底面且底面为四边形的棱柱叫做____________;
3、侧棱垂直于底面且底面为正五边形的棱柱叫做____________。
斜三棱柱
直四棱柱
正五棱柱
四棱柱
平行六面体
长方体
直平行六面体
正四棱柱
正方体
底面是
平行四边形
侧棱与底面
垂直
底面是
矩形
底面为
正方形
侧棱与底面
边长相等
平行六面体集合、长方体集合、正四棱柱集合之间存在着怎样的包含关系?
平行六面体集合
正四棱柱集合
长方体集合
例2、
下列说法中,正确的是( )
A.四棱柱是平行六面体
B.直平行六面体是长方体
C.六个面都是矩形的六面体是长方体
D.底面是矩形的四棱柱是长方体
例3、
经过长方体同一个顶点的三条棱长分别是a、b、c,那么这个长方体的对角线长是多少?
A
B
C
D
练习题一
(1)任意一个直棱柱去掉两个底面,沿任意一条侧棱剪开,然后放在一个平面上展开,它是什么样的平面图形?
(2)长方体是不是四棱柱?直四棱柱是不是长方体?
(3)正方体集合记为A,长方体集合记为B,直棱柱集合记为C,棱柱集合记为D,写出这四个集合之间的关系。
练习题二
(1).在棱柱中 ( )
A.只有两个面平行
B.所有的棱都相等
C.所有的面都是平行四边形
D.两底面平行,且各侧棱也平行
(2).下列命题中正确的是 ( )
A.四棱柱是平行六面体
B.直平行六面体是长方体
C.底面是矩形的四棱柱是长方体
D.六个面都是矩形的六面体是长方体
(3).下面没有体对角线的一种几何体是 ( )
A.三棱柱
B.四棱柱
C.五棱柱
D.六棱柱
A
课堂小结
多面体的概念
棱柱的概念与分类
思考题
如图所示,在正三棱柱ABC- 中,AB=3,
=4,M为 的中点,P是BC上一点,且由点P沿棱柱侧面经过棱 到点M最短路线长为 ,设这条最短路线与 的交点为N。求:该三棱柱的侧面展开图的对角线长; PC和NC的长。
C
B
N
A
M
P
棱柱、棱锥和棱台
的结构特征
多面体是由若干个平面所围成的几何体。多面体最少4个面
A
B
C
D
A`
B`
C`
D`
棱
面
截面
顶点
对角线
把一个多面体的任何一个面延展为平面,如果其余各面都
在这个平面的同一侧,则这样的多面体叫凸多面体。
判断下列几何体哪些是多面体?
A
B
C
D
A`
B`
C`
D`
底
面
侧
面
侧
棱
高
棱柱可以看成一个多边形(包括图形围成的平面部分)上各点都沿着同一个方向移动相同的距离所形成的几何体。
棱柱的性质
自主探究1、棱柱上下两个底面关系如何,侧棱之间关系 如何?
性质1:棱柱上下两个底面互相平行,侧棱互相平行。
自主探究2、棱柱上、下两个底面的形状大小如何?各侧 面的形状如何?
性质2、棱柱上下两个底面全等,各侧面都是平行四边形。
例1
1、下列命题中,正确的是( )
A.有两个面互相平行,其余各面都是四边形的几何体叫棱柱
B.棱柱中互相平行的两个面叫做棱柱的底面
C.棱柱的侧面是平行四边形,而底面不是平行四边形
D.棱柱的侧棱都相等,侧面是平行四边形
棱柱的分类
按底面多边形分类:
底面是三角形、四边形、五边形......分别叫做三棱柱、四棱柱、五棱柱......
按侧棱与底面关系分类:
侧棱与底面垂直的棱柱叫做直棱柱。
侧棱与底面不垂直的棱柱叫做斜棱柱。
特殊棱柱
底面是正多边形的直棱柱叫做正棱柱。
底面是平行四边形的棱柱叫平行六面体。
练习
1、侧棱不垂直于底面且底面为三角形的棱柱叫做___________;
2、侧棱垂直于底面且底面为四边形的棱柱叫做____________;
3、侧棱垂直于底面且底面为正五边形的棱柱叫做____________。
斜三棱柱
直四棱柱
正五棱柱
四棱柱
平行六面体
长方体
直平行六面体
正四棱柱
正方体
底面是
平行四边形
侧棱与底面
垂直
底面是
矩形
底面为
正方形
侧棱与底面
边长相等
平行六面体集合、长方体集合、正四棱柱集合之间存在着怎样的包含关系?
平行六面体集合
正四棱柱集合
长方体集合
例2、
下列说法中,正确的是( )
A.四棱柱是平行六面体
B.直平行六面体是长方体
C.六个面都是矩形的六面体是长方体
D.底面是矩形的四棱柱是长方体
例3、
经过长方体同一个顶点的三条棱长分别是a、b、c,那么这个长方体的对角线长是多少?
A
B
C
D
练习题一
(1)任意一个直棱柱去掉两个底面,沿任意一条侧棱剪开,然后放在一个平面上展开,它是什么样的平面图形?
(2)长方体是不是四棱柱?直四棱柱是不是长方体?
(3)正方体集合记为A,长方体集合记为B,直棱柱集合记为C,棱柱集合记为D,写出这四个集合之间的关系。
练习题二
(1).在棱柱中 ( )
A.只有两个面平行
B.所有的棱都相等
C.所有的面都是平行四边形
D.两底面平行,且各侧棱也平行
(2).下列命题中正确的是 ( )
A.四棱柱是平行六面体
B.直平行六面体是长方体
C.底面是矩形的四棱柱是长方体
D.六个面都是矩形的六面体是长方体
(3).下面没有体对角线的一种几何体是 ( )
A.三棱柱
B.四棱柱
C.五棱柱
D.六棱柱
A
课堂小结
多面体的概念
棱柱的概念与分类
思考题
如图所示,在正三棱柱ABC- 中,AB=3,
=4,M为 的中点,P是BC上一点,且由点P沿棱柱侧面经过棱 到点M最短路线长为 ,设这条最短路线与 的交点为N。求:该三棱柱的侧面展开图的对角线长; PC和NC的长。
C
B
N
A
M
P
