高中数学人教新课标B版必修2--《1.1.3 圆柱、圆锥、圆台和球》 课件(共27张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修2--《1.1.3 圆柱、圆锥、圆台和球》 课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 00:00:00 | ||
图片预览





文档简介
(共27张PPT)
O
O1
O1
1、定义:以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱。
(1)旋转轴叫做圆柱的轴。
(2) 垂直于轴的边旋转而成的曲面叫做圆柱的底面。
(3)平行于轴的边旋转而成的曲面叫做圆柱的侧面。
(4)无论旋转到什么位置不垂直于轴的边都叫做圆柱的母线。
圆柱
2、表示:如圆柱OO1。
A
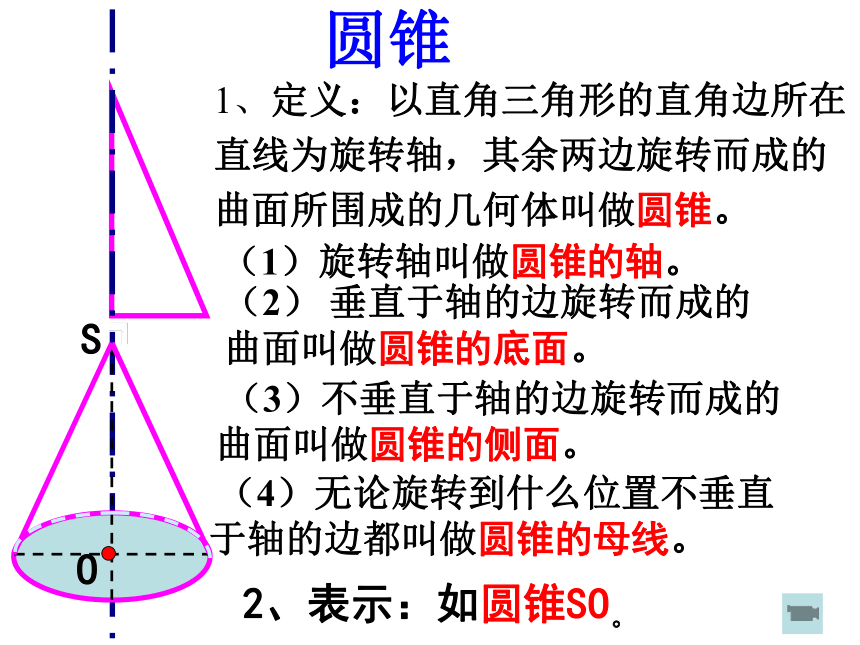
1、定义:以直角三角形的直角边所在直线为旋转轴,其余两边旋转而成的曲面所围成的几何体叫做圆锥。
(1)旋转轴叫做圆锥的轴。
(2) 垂直于轴的边旋转而成的曲面叫做圆锥的底面。
(3)不垂直于轴的边旋转而成的曲面叫做圆锥的侧面。
(4)无论旋转到什么位置不垂直于轴的边都叫做圆锥的母线。
圆锥
2、表示:如圆锥SO。
O
O
S
O
O1
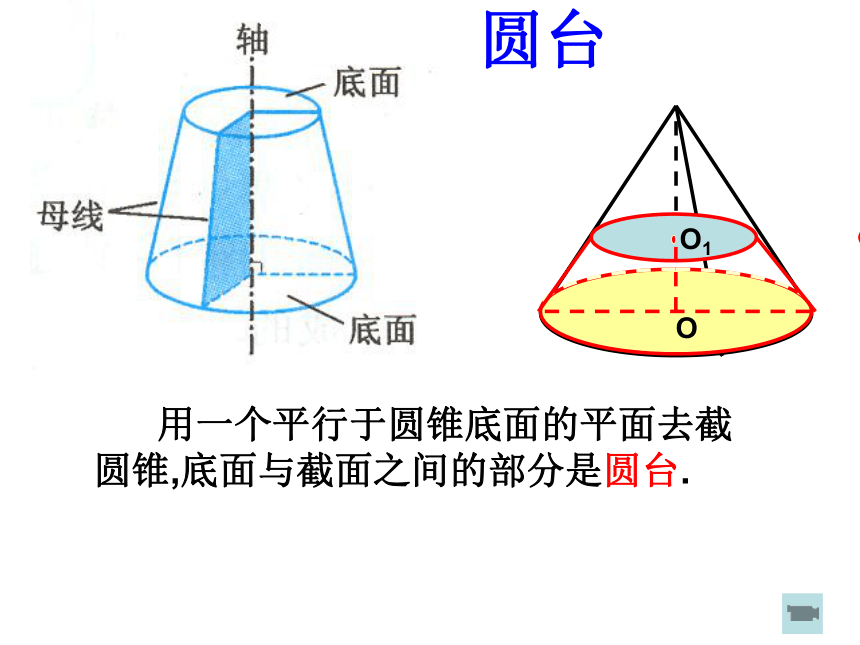
用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分是圆台.
圆台
一条平面曲线绕着它所在的平面内的一条定直线旋转所围成的几何体叫作旋转体。
旋转体
轴
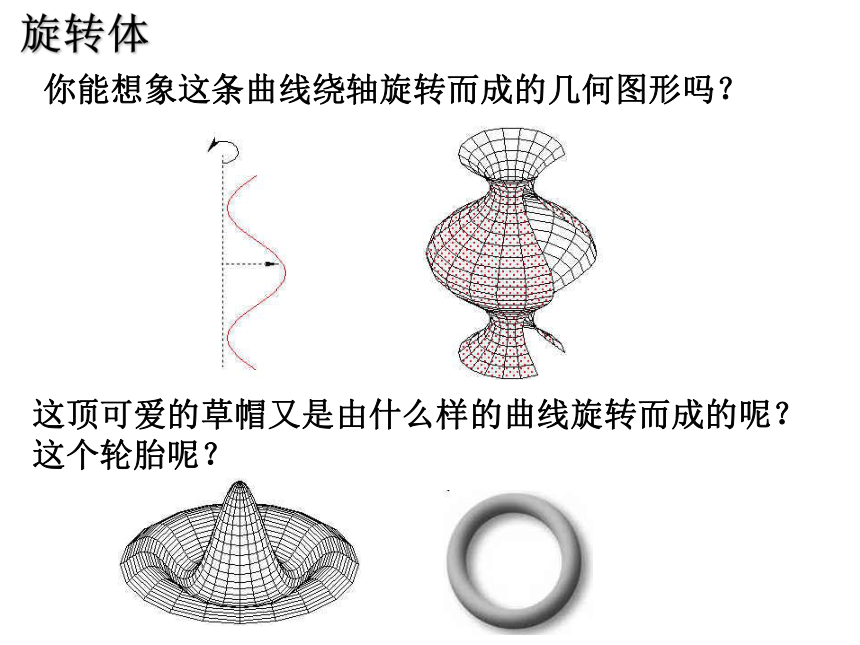
你能想象这条曲线绕轴旋转而成的几何图形吗?
这顶可爱的草帽又是由什么样的曲线旋转而成的呢? 这个轮胎呢?
旋转体
思考:圆柱、圆锥和圆台都是旋转体,当底面发生变化时,它们能否互相转化?
上底扩大
上底缩小
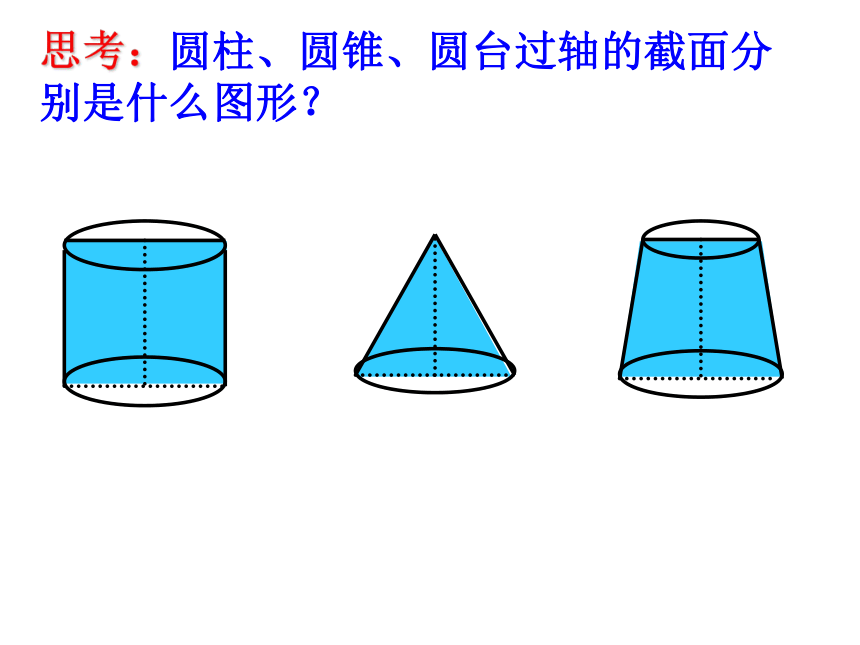
思考:圆柱、圆锥、圆台过轴的截面分别是什么图形?
例1. 用一个平行圆锥底面的平面截这个 圆锥,截得圆台上下底面半径的比是1:4,截去的圆锥的母线长是3cm,求圆台的母线长。
A
S
O
S
A
y
4x
x
解: 设圆台的母线长为y,
截得的圆锥底面与原圆锥底面半径
分别是x,4x,根据相似三角形的性质得
O
球心
球的半径
A
B
1、球的定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体叫做球体,简称球。
2、球的表示:用表示球心的字母表示,如球O
球:
球的直径
O
注意:
球体:
球面:
空间中到一个定点的距离等于定长的点的集合
思考:用一个平面去截一个球,截面是什么图形?
圆面
d
r
R
球面被经过球心的平面截得的圆叫做球的大圆。
球面被不过球心的平面截得的圆叫球的小圆。
半圆面旋转一周形成的几何体
思考与讨论:在平面几何中,你学习了直线与圆的位置关系,那么平面与球 的位置关系如何?
90°
60°
40°
20°
0°
20°
40°
60°
90°
66.5°
23.5° 南回归线
23.5°
66.5°
北极圈
北回归线
赤道
南极圈
30°
60°
90°
120°
150°
经度和纬度:
O
A
P
北极
南极
G
R
r
P地的纬度就是经过P点的球半径和赤道平面所成的线面角∠POA的度数
在球面上,两点之间的最短距离,就是经过这两点的大圆在这两点间的一段劣弧的长度。
球面距离
A
B
N
O
练习:1、球O的半径为2,它的表面上有两点A、B,∠AOB=600,
则A、B两点间的球面距离为( )
A、π B、2π
C、2π/3 D、π/2
C
例2 我国首都北京靠近北纬40 ° ,求北纬线的长度(单位:km,地球半径约6370km,结果保留四位有效数字)。
O
A
K
B
40 °
解:作轴截面如图,A是北纬40°圈上的一点,AK是它的半径,所以OK⊥AK 。设c是北纬40°的纬线长。
∵∠AOB=∠OAK=40°,
A北京
O
K
∴c= 2 π ×AK =
答:北纬40°纬线的长度3.066×104km
≈3.066×104(km)
≈2×3.1416×6370×0.7660
2π·OAcos∠OAK
组合体
日常生活中我们常用到的日用品,比如:消毒液、暖瓶、洗洁精等的主要几何结构特征是什么?
简单组合体
由柱、锥、台、球组成了一些简单的组合体.认识它们的结构特征要注意整体与部分的关系.
圆柱
圆台
圆柱
走在街上会看到一些物体,它们的主要几何结构特征是什么?
简单组合体
一些螺母、带盖螺母又是有什么主要的几何结构特征呢?
简单组合体
蒙古大草原上遍布蒙古包,那么蒙古包的主要几何结构特征是什么?
简单组合体
居民的住宅又有什么主要几何结构特征?
简单组合体
下图是著名的中央电视塔和天坛,你能说说它们的主要几何结构特征吗?
你能从旋转体的概念说说它们是由什么图形旋转而成的吗?
简单组合体
数学在生活中无处不在,培养在生活中不断的用数学的眼光看问题,会逐渐激发学数学的兴趣,增强数学地分析问题、解决问题的能力.
生活与数学
生活与数学
几何体的分类
柱体
锥体
台体
球
多面体
旋转体
小结
O
O1
O1
1、定义:以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱。
(1)旋转轴叫做圆柱的轴。
(2) 垂直于轴的边旋转而成的曲面叫做圆柱的底面。
(3)平行于轴的边旋转而成的曲面叫做圆柱的侧面。
(4)无论旋转到什么位置不垂直于轴的边都叫做圆柱的母线。
圆柱
2、表示:如圆柱OO1。
A
1、定义:以直角三角形的直角边所在直线为旋转轴,其余两边旋转而成的曲面所围成的几何体叫做圆锥。
(1)旋转轴叫做圆锥的轴。
(2) 垂直于轴的边旋转而成的曲面叫做圆锥的底面。
(3)不垂直于轴的边旋转而成的曲面叫做圆锥的侧面。
(4)无论旋转到什么位置不垂直于轴的边都叫做圆锥的母线。
圆锥
2、表示:如圆锥SO。
O
O
S
O
O1
用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分是圆台.
圆台
一条平面曲线绕着它所在的平面内的一条定直线旋转所围成的几何体叫作旋转体。
旋转体
轴
你能想象这条曲线绕轴旋转而成的几何图形吗?
这顶可爱的草帽又是由什么样的曲线旋转而成的呢? 这个轮胎呢?
旋转体
思考:圆柱、圆锥和圆台都是旋转体,当底面发生变化时,它们能否互相转化?
上底扩大
上底缩小
思考:圆柱、圆锥、圆台过轴的截面分别是什么图形?
例1. 用一个平行圆锥底面的平面截这个 圆锥,截得圆台上下底面半径的比是1:4,截去的圆锥的母线长是3cm,求圆台的母线长。
A
S
O
S
A
y
4x
x
解: 设圆台的母线长为y,
截得的圆锥底面与原圆锥底面半径
分别是x,4x,根据相似三角形的性质得
O
球心
球的半径
A
B
1、球的定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体叫做球体,简称球。
2、球的表示:用表示球心的字母表示,如球O
球:
球的直径
O
注意:
球体:
球面:
空间中到一个定点的距离等于定长的点的集合
思考:用一个平面去截一个球,截面是什么图形?
圆面
d
r
R
球面被经过球心的平面截得的圆叫做球的大圆。
球面被不过球心的平面截得的圆叫球的小圆。
半圆面旋转一周形成的几何体
思考与讨论:在平面几何中,你学习了直线与圆的位置关系,那么平面与球 的位置关系如何?
90°
60°
40°
20°
0°
20°
40°
60°
90°
66.5°
23.5° 南回归线
23.5°
66.5°
北极圈
北回归线
赤道
南极圈
30°
60°
90°
120°
150°
经度和纬度:
O
A
P
北极
南极
G
R
r
P地的纬度就是经过P点的球半径和赤道平面所成的线面角∠POA的度数
在球面上,两点之间的最短距离,就是经过这两点的大圆在这两点间的一段劣弧的长度。
球面距离
A
B
N
O
练习:1、球O的半径为2,它的表面上有两点A、B,∠AOB=600,
则A、B两点间的球面距离为( )
A、π B、2π
C、2π/3 D、π/2
C
例2 我国首都北京靠近北纬40 ° ,求北纬线的长度(单位:km,地球半径约6370km,结果保留四位有效数字)。
O
A
K
B
40 °
解:作轴截面如图,A是北纬40°圈上的一点,AK是它的半径,所以OK⊥AK 。设c是北纬40°的纬线长。
∵∠AOB=∠OAK=40°,
A北京
O
K
∴c= 2 π ×AK =
答:北纬40°纬线的长度3.066×104km
≈3.066×104(km)
≈2×3.1416×6370×0.7660
2π·OAcos∠OAK
组合体
日常生活中我们常用到的日用品,比如:消毒液、暖瓶、洗洁精等的主要几何结构特征是什么?
简单组合体
由柱、锥、台、球组成了一些简单的组合体.认识它们的结构特征要注意整体与部分的关系.
圆柱
圆台
圆柱
走在街上会看到一些物体,它们的主要几何结构特征是什么?
简单组合体
一些螺母、带盖螺母又是有什么主要的几何结构特征呢?
简单组合体
蒙古大草原上遍布蒙古包,那么蒙古包的主要几何结构特征是什么?
简单组合体
居民的住宅又有什么主要几何结构特征?
简单组合体
下图是著名的中央电视塔和天坛,你能说说它们的主要几何结构特征吗?
你能从旋转体的概念说说它们是由什么图形旋转而成的吗?
简单组合体
数学在生活中无处不在,培养在生活中不断的用数学的眼光看问题,会逐渐激发学数学的兴趣,增强数学地分析问题、解决问题的能力.
生活与数学
生活与数学
几何体的分类
柱体
锥体
台体
球
多面体
旋转体
小结
