高中数学人教新课标B版必修2--《1.1.6 棱柱、棱锥、棱台和球的表面积》 课件(共21张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修2--《1.1.6 棱柱、棱锥、棱台和球的表面积》 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 930.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
1、掌握柱、锥、台体的表面积的求法(不需要记忆公式),掌握其推导过程;
2、进一步加强空间与平面问题互相转化的思想方法的应用。
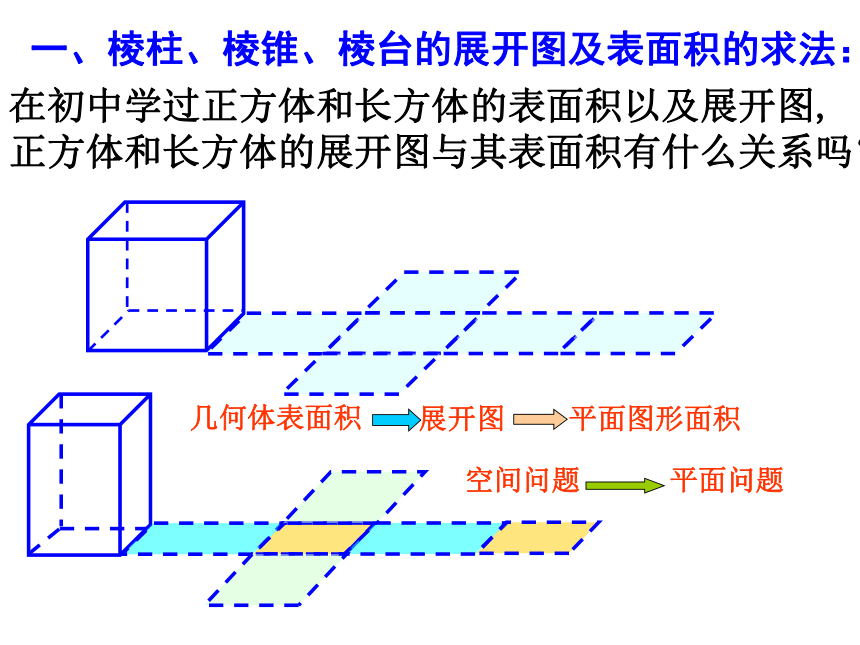
在初中学过正方体和长方体的表面积以及展开图,正方体和长方体的展开图与其表面积有什么关系吗?
几何体表面积
展开图
平面图形面积
空间问题
平面问题
一、棱柱、棱锥、棱台的展开图及表面积的求法:
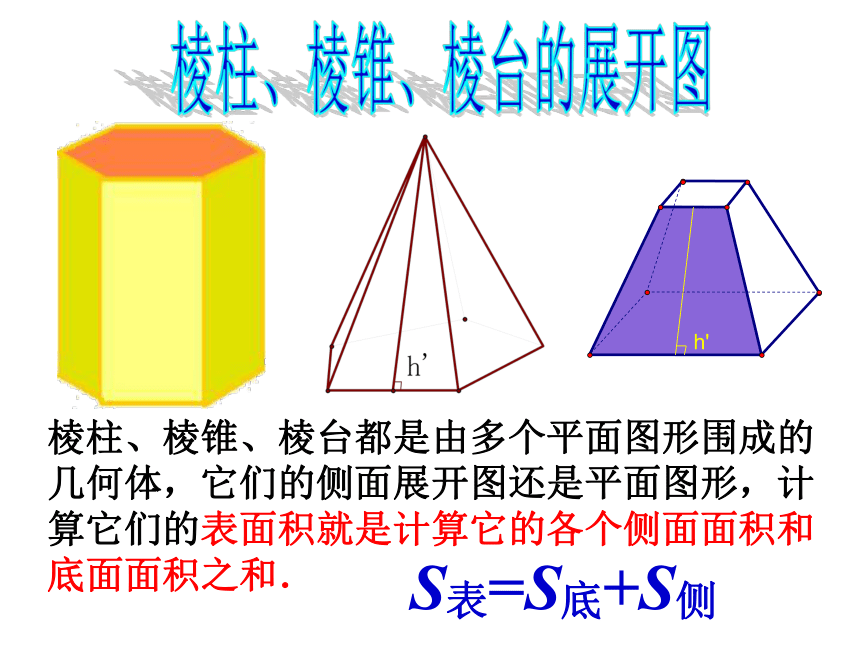
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧面展开图还是平面图形,计算它们的表面积就是计算它的各个侧面面积和底面面积之和.
h'
S表=S底+S侧
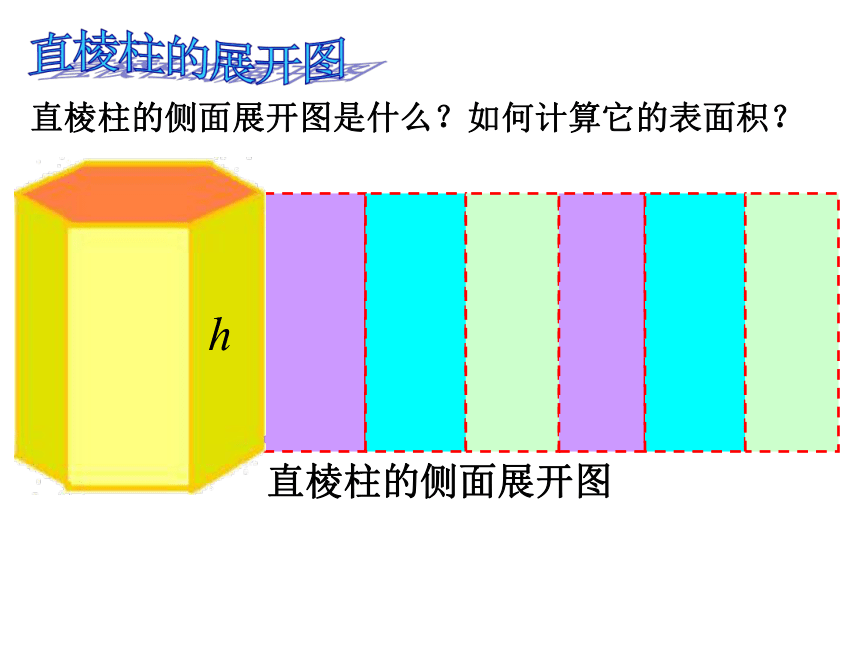
直棱柱的侧面展开图是什么?如何计算它的表面积?
h
直棱柱的侧面展开图
正棱锥的侧面展开图是什么?如何计算它的表面积?
正棱锥的侧面展开图
侧面展开
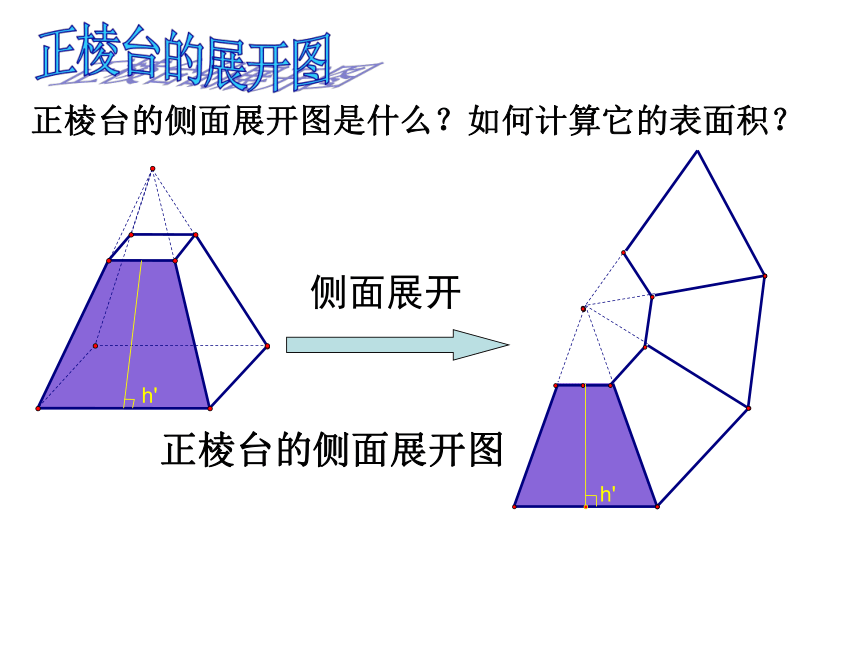
正棱台的侧面展开图是什么?如何计算它的表面积?
正棱台的侧面展开图
侧面展开
h'
h'
例1.已知棱长为a ,各面均为等边三角形的四面体S-ABC,求它的表面积 .
B
C
A
S
D
交BC于点D.
解:过点S作 ,
B
C
A
S
∵
例1.已知棱长为a ,各面均为等边三角形的四面体S-ABC,求它的表面积 .
因此,四面体S-ABC的表面积为
习题精析:
练习1.已知正四棱锥底面正方形的边长为4cm,高与斜高的夹角为
求正四棱锥的侧面积及全面积。
练习2.已知正四棱台上底面边长为4cm,侧棱和下底面边长都是8cm,求它的全面积____________
圆柱的侧面展开图是矩形
O
二、圆柱、圆锥、圆台的展开图及表面积的求法:
圆锥的侧面展开图是扇形
O
例2.若一个圆锥的轴截面是等边三角形,其面积是 ,则这个圆锥的全面积。
解:一个圆锥的轴截面是等边三角形,其面积为 ,则它的边长是a,
所以 = ,∴a=2 ,
这个圆锥的全面积是:2π+ ×2π× 1 ×2 =3π
故答案为:3π.
O
O’
圆台的侧面展开图是扇环
O
O’
侧
15cm
20cm
15cm
例3.一圆台形花盆,盆口直径20厘米,盆底直径15厘米底部渗水圆孔直径1.5厘米,盆壁长15厘米,为美化外表而涂油漆,若每平方米用100毫升油漆,涂100个这样的花盆要多少油漆?(π取3.14,结果精确到1毫升)
若每平方米用100毫升油漆,则涂100个这样的花盆要0.0999×100×100=999毫升油漆
解:由圆台的表面积公式可得花盆的表面积为
练习:看图回答问题
O
O’
O
O
圆柱、圆锥、圆台的表面积公式之间有什么关系?
上底扩大
上底缩小
r/=0
r/=r
已知球的半径为R,用R表示球的表面积?
O
练习1.已知球的大圆周长为16
求这个球的表面积。
练习2.过球半径的中点,作一垂直于这条半径的截面,已知此截面的面积是
试求球的表面积。
【总一总★成竹在胸】
1.柱、锥、台体的表面积的求法;
2.将空间图形的问题转化成平面图形问题,是解决立体几何的常用方法。
1、掌握柱、锥、台体的表面积的求法(不需要记忆公式),掌握其推导过程;
2、进一步加强空间与平面问题互相转化的思想方法的应用。
在初中学过正方体和长方体的表面积以及展开图,正方体和长方体的展开图与其表面积有什么关系吗?
几何体表面积
展开图
平面图形面积
空间问题
平面问题
一、棱柱、棱锥、棱台的展开图及表面积的求法:
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧面展开图还是平面图形,计算它们的表面积就是计算它的各个侧面面积和底面面积之和.
h'
S表=S底+S侧
直棱柱的侧面展开图是什么?如何计算它的表面积?
h
直棱柱的侧面展开图
正棱锥的侧面展开图是什么?如何计算它的表面积?
正棱锥的侧面展开图
侧面展开
正棱台的侧面展开图是什么?如何计算它的表面积?
正棱台的侧面展开图
侧面展开
h'
h'
例1.已知棱长为a ,各面均为等边三角形的四面体S-ABC,求它的表面积 .
B
C
A
S
D
交BC于点D.
解:过点S作 ,
B
C
A
S
∵
例1.已知棱长为a ,各面均为等边三角形的四面体S-ABC,求它的表面积 .
因此,四面体S-ABC的表面积为
习题精析:
练习1.已知正四棱锥底面正方形的边长为4cm,高与斜高的夹角为
求正四棱锥的侧面积及全面积。
练习2.已知正四棱台上底面边长为4cm,侧棱和下底面边长都是8cm,求它的全面积____________
圆柱的侧面展开图是矩形
O
二、圆柱、圆锥、圆台的展开图及表面积的求法:
圆锥的侧面展开图是扇形
O
例2.若一个圆锥的轴截面是等边三角形,其面积是 ,则这个圆锥的全面积。
解:一个圆锥的轴截面是等边三角形,其面积为 ,则它的边长是a,
所以 = ,∴a=2 ,
这个圆锥的全面积是:2π+ ×2π× 1 ×2 =3π
故答案为:3π.
O
O’
圆台的侧面展开图是扇环
O
O’
侧
15cm
20cm
15cm
例3.一圆台形花盆,盆口直径20厘米,盆底直径15厘米底部渗水圆孔直径1.5厘米,盆壁长15厘米,为美化外表而涂油漆,若每平方米用100毫升油漆,涂100个这样的花盆要多少油漆?(π取3.14,结果精确到1毫升)
若每平方米用100毫升油漆,则涂100个这样的花盆要0.0999×100×100=999毫升油漆
解:由圆台的表面积公式可得花盆的表面积为
练习:看图回答问题
O
O’
O
O
圆柱、圆锥、圆台的表面积公式之间有什么关系?
上底扩大
上底缩小
r/=0
r/=r
已知球的半径为R,用R表示球的表面积?
O
练习1.已知球的大圆周长为16
求这个球的表面积。
练习2.过球半径的中点,作一垂直于这条半径的截面,已知此截面的面积是
试求球的表面积。
【总一总★成竹在胸】
1.柱、锥、台体的表面积的求法;
2.将空间图形的问题转化成平面图形问题,是解决立体几何的常用方法。
