5单元圆的面积(3课时)(课件)- 六年级上册数学 人教版(30张PPT)
文档属性
| 名称 | 5单元圆的面积(3课时)(课件)- 六年级上册数学 人教版(30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 00:00:00 | ||
图片预览








文档简介
(共30张PPT)
《圆的面积》
半径为2米的圆形草地
小马能吃到多大一块青草?
圆所占平面的大小叫做圆的面积。
什么是圆的面积?
关于圆的面积你还想知道什么?
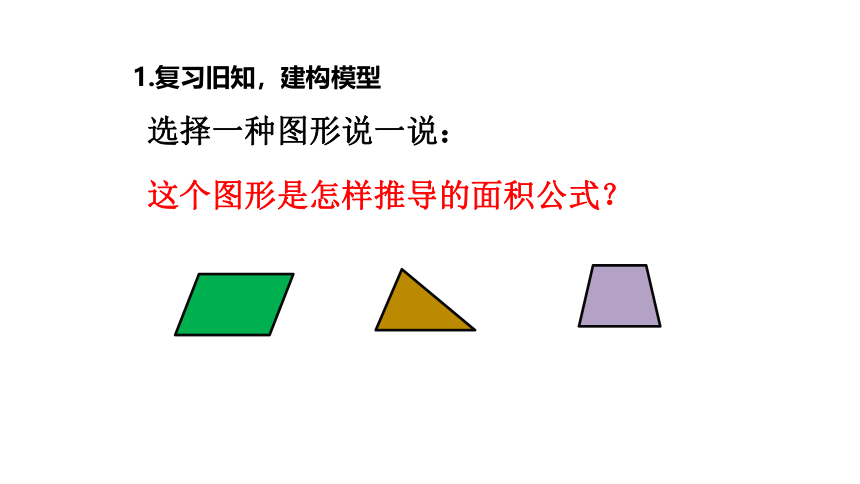
1.复习旧知,建构模型
选择一种图形说一说:
这个图形是怎样推导的面积公式?
1.复习旧知,建构模型
S三角形=a×h÷2
S梯形=(a+b)×h÷2
→
→
→
→
S平行四边形=a×h
→
→
它们的面积公式都是采用什么思路推导出来的?
小结:它们用转化的方法,找到转化前后图形的联系,然后推导公式。
2.讨论转化,操作想象
问:(1)要想得到圆的面积公式,你有什么疑惑?
(2)圆是曲边图形,怎么转化成直边图形?
(3)猜想圆能转化成什么图形?
生:平行四边形、长方形、三角形……
2.讨论转化,操作想象
小组讨论:圆怎样转化成平行四边形?
汇报交流:
生:……
追问:怎样转化?从哪剪?为什么这样剪?还能分成多少份?
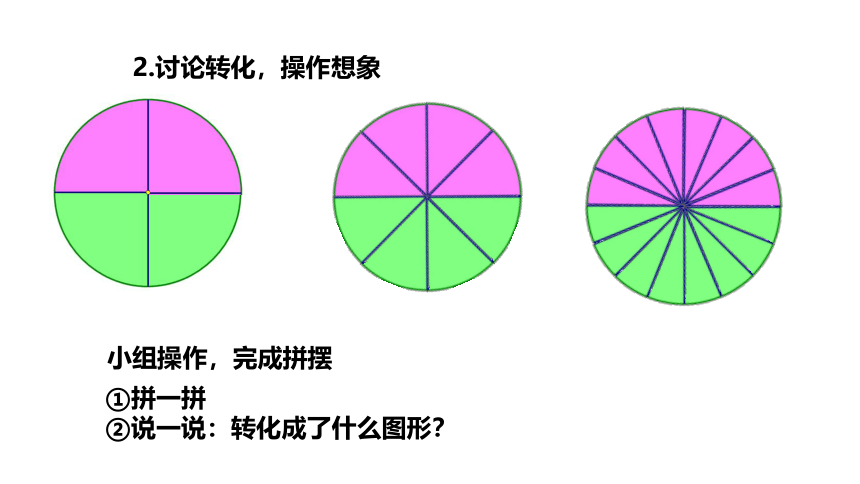
2.讨论转化,操作想象
小组操作,完成拼摆
①拼一拼
②说一说:转化成了什么图形?
2.讨论转化,操作想象
小组展示(展示平均分成4份、8份、16份拼摆后的作品。)
观察这三幅图,你发现了什么?
有没有什么办法使它变得更像平行四边形一些?
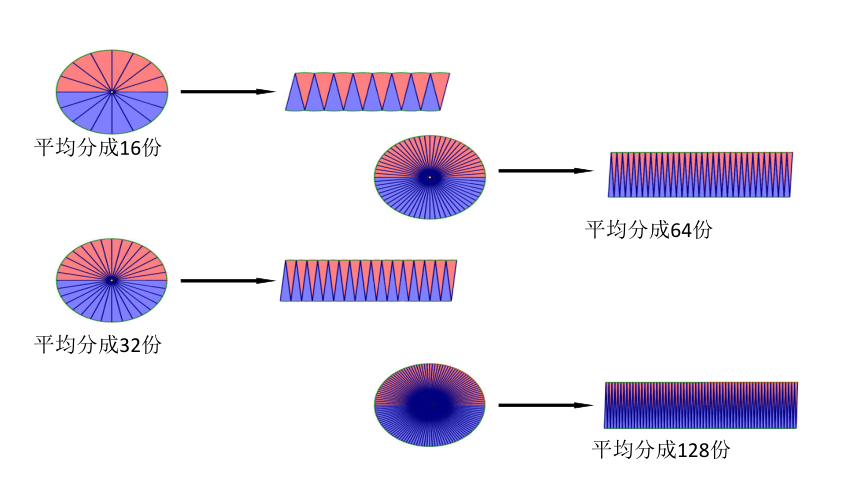
平均分成16份
平均分成32份
平均分成64份
平均分成128份
3.找圆与长方形的联系
小组合作,推导公式
1.讨论:
转化后的长方形和原的圆之间有什么联系?
2.推导圆的面积公式
3. 说一说:
圆的面积公式推导过程。
师:长方形与圆有什么联系?
4.圆的面积公式推导
生:长方形的面积等于圆的面积
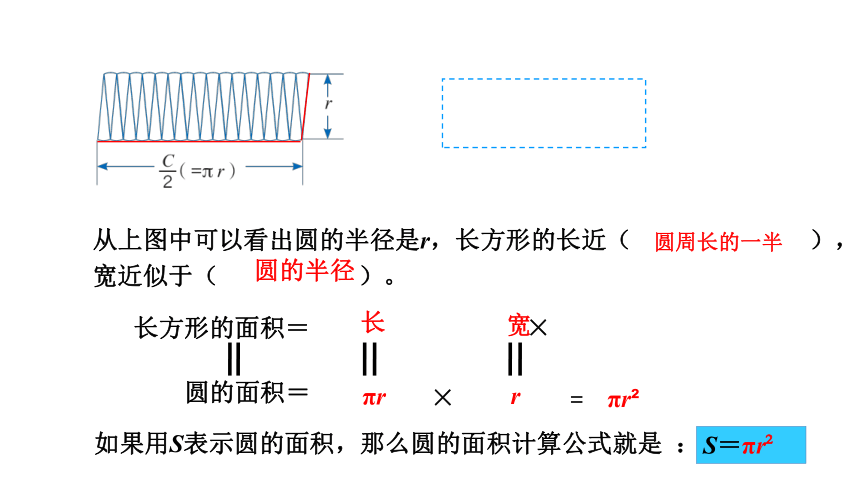
从上图中可以看出圆的半径是r,长方形的长近( ),宽近似于( )。
长方形的面积= ×
圆的面积=
如果用S表示圆的面积,那么圆的面积计算公式就是 :
圆周长的一半
圆的半径
长
宽
πr
r
πr
S=πr
×
=
1.知道半径、直径、周长求面积
师:已知直径怎么求圆的面积?
生:……
师:已知周长呢?
2.生活运用
公园草地上一个自动旋转喷灌装置的射程是10m,它能灌溉的面积是多少?
S = πr 2
=3.14 ×102
=3.14 ×(10 ×10 )
=3.14 ×100
=314(cm 2)
答:它的灌溉面积是314平方厘米。
1.数学故事:历史上圆的面积求解方法
我国古代的数学家祖冲之,从圆内接正六边形入手,让边数成倍增加,用圆内接正多边形的面积去逼近圆面积。
1.数学故事:历史上圆的面积求解方法
古希腊的数学家,从圆内接正多边形和外切正多边形同时入手,不断增加它们的边数,从里外两个方面去逼近圆面积。
1.数学故事:历史上圆的面积求解方法
古印度的数学家,采用类似切西瓜的办法,把圆切成许多小瓣,再把这些小瓣对接成一个长方形,用长方形的面积去代替圆面积。
众多的古代数学家煞费苦心,巧妙构思,为求圆面积作出了十分宝贵的贡献。为后人解决这个问题开辟了道路。
2.回顾小结:这节课我们怎样学的圆的面积?
C
1
4
4r
三角形的面积 = 底×高÷2
圆的面积
4r
= × ÷2
=πr2
πr
1
2
C
5
16
C
3
16
梯形的面积=(上底+下底)×高÷2
圆的面积
2r
= × ÷2
=πr2
2r
πr
S三角形=a×h÷2
S梯形=(a+b)×h÷2
→
→
→
→
S平行四边形=a×h
→
→
→
→
S圆=πr2
转化
找联系
推导公式
《圆的面积》
半径为2米的圆形草地
小马能吃到多大一块青草?
圆所占平面的大小叫做圆的面积。
什么是圆的面积?
关于圆的面积你还想知道什么?
1.复习旧知,建构模型
选择一种图形说一说:
这个图形是怎样推导的面积公式?
1.复习旧知,建构模型
S三角形=a×h÷2
S梯形=(a+b)×h÷2
→
→
→
→
S平行四边形=a×h
→
→
它们的面积公式都是采用什么思路推导出来的?
小结:它们用转化的方法,找到转化前后图形的联系,然后推导公式。
2.讨论转化,操作想象
问:(1)要想得到圆的面积公式,你有什么疑惑?
(2)圆是曲边图形,怎么转化成直边图形?
(3)猜想圆能转化成什么图形?
生:平行四边形、长方形、三角形……
2.讨论转化,操作想象
小组讨论:圆怎样转化成平行四边形?
汇报交流:
生:……
追问:怎样转化?从哪剪?为什么这样剪?还能分成多少份?
2.讨论转化,操作想象
小组操作,完成拼摆
①拼一拼
②说一说:转化成了什么图形?
2.讨论转化,操作想象
小组展示(展示平均分成4份、8份、16份拼摆后的作品。)
观察这三幅图,你发现了什么?
有没有什么办法使它变得更像平行四边形一些?
平均分成16份
平均分成32份
平均分成64份
平均分成128份
3.找圆与长方形的联系
小组合作,推导公式
1.讨论:
转化后的长方形和原的圆之间有什么联系?
2.推导圆的面积公式
3. 说一说:
圆的面积公式推导过程。
师:长方形与圆有什么联系?
4.圆的面积公式推导
生:长方形的面积等于圆的面积
从上图中可以看出圆的半径是r,长方形的长近( ),宽近似于( )。
长方形的面积= ×
圆的面积=
如果用S表示圆的面积,那么圆的面积计算公式就是 :
圆周长的一半
圆的半径
长
宽
πr
r
πr
S=πr
×
=
1.知道半径、直径、周长求面积
师:已知直径怎么求圆的面积?
生:……
师:已知周长呢?
2.生活运用
公园草地上一个自动旋转喷灌装置的射程是10m,它能灌溉的面积是多少?
S = πr 2
=3.14 ×102
=3.14 ×(10 ×10 )
=3.14 ×100
=314(cm 2)
答:它的灌溉面积是314平方厘米。
1.数学故事:历史上圆的面积求解方法
我国古代的数学家祖冲之,从圆内接正六边形入手,让边数成倍增加,用圆内接正多边形的面积去逼近圆面积。
1.数学故事:历史上圆的面积求解方法
古希腊的数学家,从圆内接正多边形和外切正多边形同时入手,不断增加它们的边数,从里外两个方面去逼近圆面积。
1.数学故事:历史上圆的面积求解方法
古印度的数学家,采用类似切西瓜的办法,把圆切成许多小瓣,再把这些小瓣对接成一个长方形,用长方形的面积去代替圆面积。
众多的古代数学家煞费苦心,巧妙构思,为求圆面积作出了十分宝贵的贡献。为后人解决这个问题开辟了道路。
2.回顾小结:这节课我们怎样学的圆的面积?
C
1
4
4r
三角形的面积 = 底×高÷2
圆的面积
4r
= × ÷2
=πr2
πr
1
2
C
5
16
C
3
16
梯形的面积=(上底+下底)×高÷2
圆的面积
2r
= × ÷2
=πr2
2r
πr
S三角形=a×h÷2
S梯形=(a+b)×h÷2
→
→
→
→
S平行四边形=a×h
→
→
→
→
S圆=πr2
转化
找联系
推导公式
