苏科版物理九年级上册同步学案:11.1 杠杆(有答案)
文档属性
| 名称 | 苏科版物理九年级上册同步学案:11.1 杠杆(有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 280.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-25 11:09:14 | ||
图片预览




文档简介
一、杠 杆
【新知梳理】
一、杠杆
1.定义:物理学中,将在 可绕一 转动的硬棒称为杠杆.
2.杠杆的五要素(如图所示)
支点:杠杆绕着转动的点,常用O来表示.
动力:使杠杆 的力,常用F1来表示.
阻力: 杠杆转动的力,常用F2来表示.
动力臂:从支点到 的距离,常用l1来表示.
阻力臂:从支点到 的距离,常用l2来表示.
(
二
)二、杠杆的平衡条件
1.杠杆平衡
杠杆 或 ,我们就说此时杠杆处于平衡状态.
[说明] 杠杆在水平位置或倾斜位置静止时都处于平衡状态.
2.探究杠杆的平衡条件
(1)实验器材:所需的器材除了杠杆、支架、细线、钩码外,还需要 .
(2)实验装置:如图所示.
(3)实验步骤
①组装、调节杠杆:把杠杆中点支在支架上,调节杠杆两端的螺母使杠杆在 位置平衡.
②在杠杆左边挂上一定数量的钩码,用弹簧测力计在某一位置沿 方向拉住杠杆,使杠杆在 位置平衡,记录钩码对杠杆的拉力即阻力F2、阻力臂l2、弹簧测力计的拉力即动力F1、动力臂l1,并填入实验数据记录表中.
③不断改变钩码的个数和钩码悬挂的位置,使杠杆在水平位置重新平衡,重复步骤②,记录对应的F2、l2、F1、l1,并填入实验数据记录表中.
(4)实验数据记录表
实验次数 动力F1/N 动力臂l1/m 阻力F2/N 阻力臂l2/m
1
2
3
(5)分析论证:分析上述表格中的数据,运用加减乘除运算,找出动力F1、动力臂l1、阻力F2、阻力臂l2之间存在怎样的关系.
(6)实验结论:杠杆的平衡条件是 ,表达式是 ,这个平衡条件也称为杠杆原理.
(7)评估交流
①把质量分布均匀的杠杆的中点作为支点,其目的是消除 对实验的影响.实验前,杠杆左端下沉,则应将两端的平衡螺母向 调节,直到杠杆在水平位置平衡.
②在实验过程中使杠杆在水平位置平衡,目的是便于 .
③实验中改变钩码的个数或悬挂的位置进行多次实验,目的是 .
④若改变弹簧测力计拉力的方向,仍使杠杆在水平位置平衡,弹簧测力计的示数将 ,原因是 发生改变.
三、杠杆的分类
类型 示意图 力臂关系 力的关系 特点 应用
省力杠杆 l1 l2 F1 F2 省力但费距离 铡刀、羊角锤
费力杠杆 l1 l2 F1 F2 费力但省距离 筷子、钓鱼竿
等臂杠杆 l1 l2 F1 F2 既不省力也不省距离,既不费力也不费距离 天平
【应用示例】
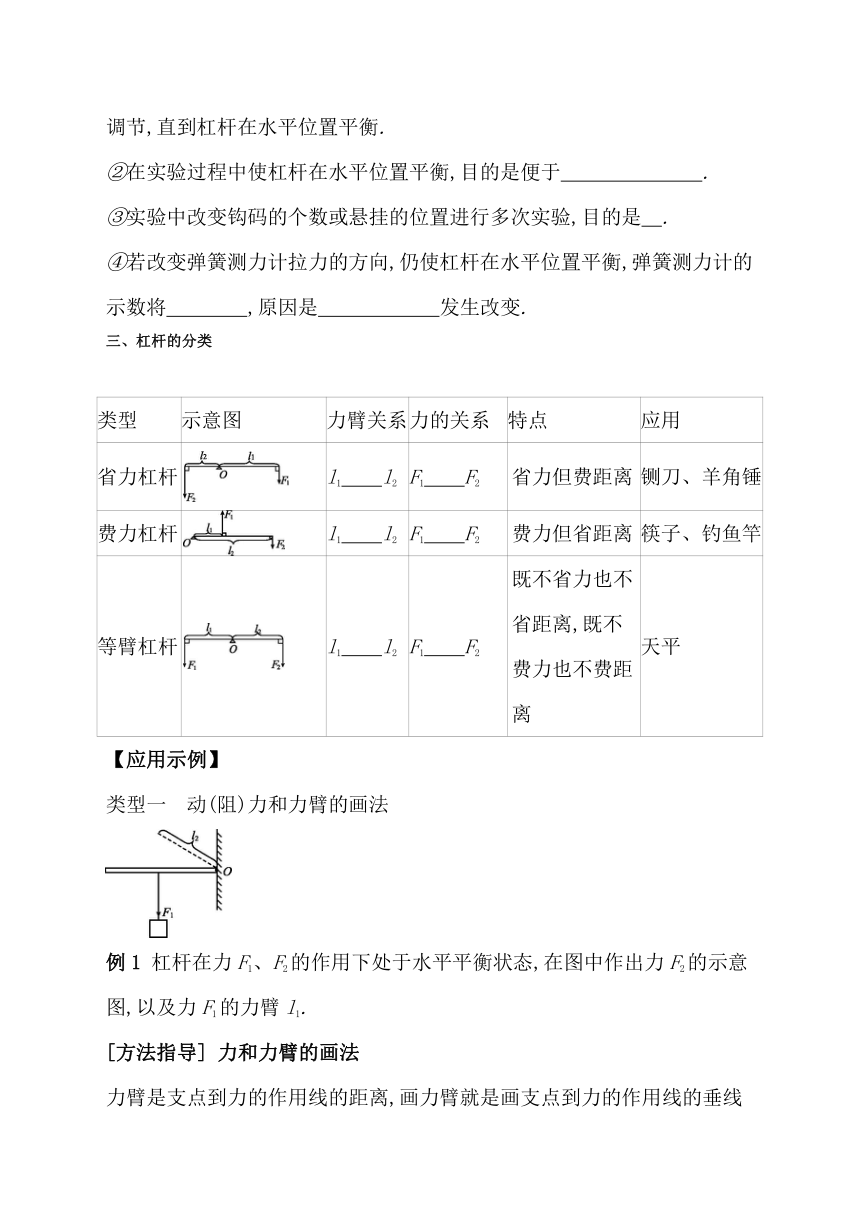
类型一 动(阻)力和力臂的画法
例1 杠杆在力F1、F2的作用下处于水平平衡状态,在图中作出力F2的示意图,以及力F1的力臂l1.
[方法指导] 力和力臂的画法
力臂是支点到力的作用线的距离,画力臂就是画支点到力的作用线的垂线段.
(1)根据已知力画对应力臂的步骤
(2)根据已知力臂画对应力的示意图的步骤:①作力的作用线,即过力臂的非支点端作力臂的垂线(虚线表示).②确定力的作用点(力的作用线与杠杆的交点).③确定力的方向,即根据动力和阻力使杠杆转动方向相反的特点,确定力的方向.④作力的示意图,即从力的作用点出发沿着力的方向作出力的示意图.
类型二 探究杠杆的平衡条件
例2 [2020-2021学年南京期中] 如图所示是小明用刻度均匀、质量分布也均匀的杠杆进行“探究杠杆平衡条件”的实验,每个钩码质量相等,杠杆上的数字所对应的单位为cm.
(1)将杠杆的中点置于支架上,当杠杆静止时,发现杠杆左端下沉,他将杠杆左端平衡螺母向右调节到最大限度后,杠杆左端仍有轻微下沉,这时他应将右端的平衡螺母向 端调节,才能使杠杆在水平位置平衡.这样既方便读取 大小,也可以消除 对实验的影响.
(2)图甲是他在探究过程中的一个情景,接下来他在两边钩码的下方各加两个相同的钩码,为了使杠杆在水平位置平衡,他应将右端钩码移动到右端 cm刻度线处.
(3)若杠杆的重心恰好处于杠杆的支点处,当杠杆在图甲的水平位置平衡后,用手使杠杆缓慢地转过一个角度(如图乙所示)后松手,杠杆 (选填“能”或“不能”)保持静止.
(4)小明通过不断改变两端所挂钩码的个数和位置,使杠杆在水平位置平衡,并记录各次实验数据,通过对数据分析后可以得出结论:动力×支点到动力作用点的距离=阻力×支点到阻力作用点的距离.与老师交流后,他增加一个弹簧测力计又做了如图所示的A、B、C三次实验.
①用弹簧测力计进行图A操作后,在图B操作前应该先 .
②A、B、C三次实验操作,图 所示实验能直接说明原先结论是错误的,图 中测力计示数最大.
[实验点拨] (1)杠杆在任意位置静止,都处于平衡状态.(2)实验前调节杠杆在水平位置平衡,是为了消除杠杆自重对实验的影响.(3)实验过程中调节杠杆在水平位置平衡,是为了便于测量力臂.
类型三 杠杆的分类
例3 如图所示的工具中,在使用时属于费力杠杆的是 ( )
[方法指导] 两种方法判断实际生活中杠杆的类型
方法1 : 先寻找杠杆的支点、动力作用点及阻力作用点,进而粗略判断出动力臂和阻力臂的大小关系,得出杠杆的类型.
方法2 : 根据杠杆使用的目的进行判断,若是为了省力,则是省力杠杆;若是为了省距离,则是费力杠杆.
类型四 最大力臂、最小力问题
例4 如图所示,在杠杆AOB的A端挂一重物G,要使杠杆在图中位置平衡,请画出在杠杆上施加的最小动力F及其力臂l的示意图.
[方法指导] 最小力的作图方法
最小动力的作图问题,可转化为找最长动力臂的问题.找最长动力臂,一般分两种情况:
(1)在动力作用点已知的情况下,支点到动力作用点的连线就是最长动力臂.
(2)在动力作用点未知时,支点到杠杆上距支点最远点的距离就是最长动力臂.首先,确定支点和动力作用点的位置,以让两点间距离最远为依据.其次,连接支点和动力作用点,所得线段即为最长动力臂.最后,根据由力臂作对应力的方法,作出最小力的示意图,注意力的方向的选择.
类型五 杠杆的动态平衡
例5 如图所示,轻质杠杆中点悬挂一重为60 N的物体,在右端施加一竖直向上的力F,杠杆在水平位置平衡,则力F的大小是 ;保持F的方向不变,将杠杆从A位置匀速提升到B位置的过程中,力F将 (选填“变大”“变小”或“不变”).
[方法指导] 杠杆动态平衡的解题技巧
有关动态杠杆的分析和计算,可以先找几个位置(一般为两个),在这几个位置的杠杆上将力和力臂都画出来,然后应用数形结合的方法,在所画图形中结合杠杆的平衡条件及杠杆被拉起过程中的变化分析求解.
类型六 运用杠杆的平衡条件计算
例6 如图所示,用固定在墙上的三角支架ABC放置空调室外机,如果A处螺钉松脱,则支架会绕C点倾翻.已知AB长40 cm,AC长30 cm,室外机的重力为300 N,其重力作用线正好经过AB中点.
(1)求A处螺钉的水平拉力为多大.(支架重力不计)
(2)若A处螺钉的水平拉力最大为400 N,则在室外机位置不变的情况下,室外机重力不能超过多少牛
[方法指导] 利用杠杆的平衡条件分析和计算有关问题的一般步骤
(1)确定杠杆支点的位置.
(2)分析杠杆受到的动力和阻力,明确其大小和方向,并作出力的示意图.
(3)确定动力臂和阻力臂.
(4)根据杠杆的平衡条件列出关系式并分析求解.
【课堂小结】
答案
一、 杠 杆
【新知梳理】
一、1.力的作用下 固定点
2.转动 阻碍 动力作用线 阻力作用线
二、1.静止 匀速转动
2.(1)弹簧测力计 (3)①水平 ②竖直 水平
(6)动力×动力臂=阻力×阻力臂 F1l1=F2l2
(7)①杠杆自重 右 ②测量力臂 ③得出普遍规律,避免实验结论的偶然性 ④变大 动力臂
三、> < < > = =
【应用示例】
例1 如图所示
例2 (1)右 力臂 杠杆自重
(2)15 (3)能
(4)①对弹簧测力计进行调零 ②C C
(1)现在杠杆左端仍有轻微下沉,说明杠杆左端偏重,为使杠杆在水平位置平衡,应将右端的平衡螺母向右端调节,使杠杆在水平位置平衡,从而消除杠杆自重对实验的影响.(2)设一个钩码重为G,左边再加两个相同的钩码后,则左边力和力臂的乘积为F左l左=3G×20 cm,右边再加两个相同的钩码后,则右边力和力臂的乘积为F右l右=4G×l右,为了使杠杆在水平位置平衡,F左l左=F右l右,即3G×20 cm=4G×l右,所以l右=15 cm,他应将右端钩码移动到右端15 cm刻度线处.(3)杠杆的重心在支点处,将杠杆转过一个角度松手后,动力和阻力不变,动力臂和阻力臂的比值不变,仍符合F左l左=F右l右,杠杆仍然是平衡的,所以能保持静止.(4)①进行A、B两次实验时,弹簧测力计所施加的拉力的方向不同,所以图A操作后、图B操作前需要对弹簧测力计进行调零.②小明得到“动力×支点到动力作用点的距离=阻力×支点到阻力作用点的距离”,这个结论是不正确的;可在动力臂不等于支点到动力作用点的距离时,看实验结论是否成立,所以利用图C进行验证.三个图中钩码的重力及其位置均不变,图C中测力计拉力的力臂最小,所以需要用的拉力最大.
例3 A 筷子在使用过程中,动力臂小于阻力臂,是费力杠杆;瓶盖起子在使用过程中,动力臂大于阻力臂,是省力杠杆;撬棒在使用过程中,动力臂大于阻力臂,是省力杠杆;核桃夹在使用过程中,动力臂大于阻力臂,是省力杠杆.
例4 如图所示
例5 30 N 不变
例6 (1)由题知,阻力臂l2=AB=×40 cm=20 cm=0.2 m,动力臂l1=AC=30 cm=0.3 m,根据杠杆平衡条件,A处螺钉的水平拉力为
FA===200 N.
(2)若A处螺钉的水平拉力最大为400 N,根据杠杆平衡条件得,室外机的重力最大为
G'===600 N.
【新知梳理】
一、杠杆
1.定义:物理学中,将在 可绕一 转动的硬棒称为杠杆.
2.杠杆的五要素(如图所示)
支点:杠杆绕着转动的点,常用O来表示.
动力:使杠杆 的力,常用F1来表示.
阻力: 杠杆转动的力,常用F2来表示.
动力臂:从支点到 的距离,常用l1来表示.
阻力臂:从支点到 的距离,常用l2来表示.
(
二
)二、杠杆的平衡条件
1.杠杆平衡
杠杆 或 ,我们就说此时杠杆处于平衡状态.
[说明] 杠杆在水平位置或倾斜位置静止时都处于平衡状态.
2.探究杠杆的平衡条件
(1)实验器材:所需的器材除了杠杆、支架、细线、钩码外,还需要 .
(2)实验装置:如图所示.
(3)实验步骤
①组装、调节杠杆:把杠杆中点支在支架上,调节杠杆两端的螺母使杠杆在 位置平衡.
②在杠杆左边挂上一定数量的钩码,用弹簧测力计在某一位置沿 方向拉住杠杆,使杠杆在 位置平衡,记录钩码对杠杆的拉力即阻力F2、阻力臂l2、弹簧测力计的拉力即动力F1、动力臂l1,并填入实验数据记录表中.
③不断改变钩码的个数和钩码悬挂的位置,使杠杆在水平位置重新平衡,重复步骤②,记录对应的F2、l2、F1、l1,并填入实验数据记录表中.
(4)实验数据记录表
实验次数 动力F1/N 动力臂l1/m 阻力F2/N 阻力臂l2/m
1
2
3
(5)分析论证:分析上述表格中的数据,运用加减乘除运算,找出动力F1、动力臂l1、阻力F2、阻力臂l2之间存在怎样的关系.
(6)实验结论:杠杆的平衡条件是 ,表达式是 ,这个平衡条件也称为杠杆原理.
(7)评估交流
①把质量分布均匀的杠杆的中点作为支点,其目的是消除 对实验的影响.实验前,杠杆左端下沉,则应将两端的平衡螺母向 调节,直到杠杆在水平位置平衡.
②在实验过程中使杠杆在水平位置平衡,目的是便于 .
③实验中改变钩码的个数或悬挂的位置进行多次实验,目的是 .
④若改变弹簧测力计拉力的方向,仍使杠杆在水平位置平衡,弹簧测力计的示数将 ,原因是 发生改变.
三、杠杆的分类
类型 示意图 力臂关系 力的关系 特点 应用
省力杠杆 l1 l2 F1 F2 省力但费距离 铡刀、羊角锤
费力杠杆 l1 l2 F1 F2 费力但省距离 筷子、钓鱼竿
等臂杠杆 l1 l2 F1 F2 既不省力也不省距离,既不费力也不费距离 天平
【应用示例】
类型一 动(阻)力和力臂的画法
例1 杠杆在力F1、F2的作用下处于水平平衡状态,在图中作出力F2的示意图,以及力F1的力臂l1.
[方法指导] 力和力臂的画法
力臂是支点到力的作用线的距离,画力臂就是画支点到力的作用线的垂线段.
(1)根据已知力画对应力臂的步骤
(2)根据已知力臂画对应力的示意图的步骤:①作力的作用线,即过力臂的非支点端作力臂的垂线(虚线表示).②确定力的作用点(力的作用线与杠杆的交点).③确定力的方向,即根据动力和阻力使杠杆转动方向相反的特点,确定力的方向.④作力的示意图,即从力的作用点出发沿着力的方向作出力的示意图.
类型二 探究杠杆的平衡条件
例2 [2020-2021学年南京期中] 如图所示是小明用刻度均匀、质量分布也均匀的杠杆进行“探究杠杆平衡条件”的实验,每个钩码质量相等,杠杆上的数字所对应的单位为cm.
(1)将杠杆的中点置于支架上,当杠杆静止时,发现杠杆左端下沉,他将杠杆左端平衡螺母向右调节到最大限度后,杠杆左端仍有轻微下沉,这时他应将右端的平衡螺母向 端调节,才能使杠杆在水平位置平衡.这样既方便读取 大小,也可以消除 对实验的影响.
(2)图甲是他在探究过程中的一个情景,接下来他在两边钩码的下方各加两个相同的钩码,为了使杠杆在水平位置平衡,他应将右端钩码移动到右端 cm刻度线处.
(3)若杠杆的重心恰好处于杠杆的支点处,当杠杆在图甲的水平位置平衡后,用手使杠杆缓慢地转过一个角度(如图乙所示)后松手,杠杆 (选填“能”或“不能”)保持静止.
(4)小明通过不断改变两端所挂钩码的个数和位置,使杠杆在水平位置平衡,并记录各次实验数据,通过对数据分析后可以得出结论:动力×支点到动力作用点的距离=阻力×支点到阻力作用点的距离.与老师交流后,他增加一个弹簧测力计又做了如图所示的A、B、C三次实验.
①用弹簧测力计进行图A操作后,在图B操作前应该先 .
②A、B、C三次实验操作,图 所示实验能直接说明原先结论是错误的,图 中测力计示数最大.
[实验点拨] (1)杠杆在任意位置静止,都处于平衡状态.(2)实验前调节杠杆在水平位置平衡,是为了消除杠杆自重对实验的影响.(3)实验过程中调节杠杆在水平位置平衡,是为了便于测量力臂.
类型三 杠杆的分类
例3 如图所示的工具中,在使用时属于费力杠杆的是 ( )
[方法指导] 两种方法判断实际生活中杠杆的类型
方法1 : 先寻找杠杆的支点、动力作用点及阻力作用点,进而粗略判断出动力臂和阻力臂的大小关系,得出杠杆的类型.
方法2 : 根据杠杆使用的目的进行判断,若是为了省力,则是省力杠杆;若是为了省距离,则是费力杠杆.
类型四 最大力臂、最小力问题
例4 如图所示,在杠杆AOB的A端挂一重物G,要使杠杆在图中位置平衡,请画出在杠杆上施加的最小动力F及其力臂l的示意图.
[方法指导] 最小力的作图方法
最小动力的作图问题,可转化为找最长动力臂的问题.找最长动力臂,一般分两种情况:
(1)在动力作用点已知的情况下,支点到动力作用点的连线就是最长动力臂.
(2)在动力作用点未知时,支点到杠杆上距支点最远点的距离就是最长动力臂.首先,确定支点和动力作用点的位置,以让两点间距离最远为依据.其次,连接支点和动力作用点,所得线段即为最长动力臂.最后,根据由力臂作对应力的方法,作出最小力的示意图,注意力的方向的选择.
类型五 杠杆的动态平衡
例5 如图所示,轻质杠杆中点悬挂一重为60 N的物体,在右端施加一竖直向上的力F,杠杆在水平位置平衡,则力F的大小是 ;保持F的方向不变,将杠杆从A位置匀速提升到B位置的过程中,力F将 (选填“变大”“变小”或“不变”).
[方法指导] 杠杆动态平衡的解题技巧
有关动态杠杆的分析和计算,可以先找几个位置(一般为两个),在这几个位置的杠杆上将力和力臂都画出来,然后应用数形结合的方法,在所画图形中结合杠杆的平衡条件及杠杆被拉起过程中的变化分析求解.
类型六 运用杠杆的平衡条件计算
例6 如图所示,用固定在墙上的三角支架ABC放置空调室外机,如果A处螺钉松脱,则支架会绕C点倾翻.已知AB长40 cm,AC长30 cm,室外机的重力为300 N,其重力作用线正好经过AB中点.
(1)求A处螺钉的水平拉力为多大.(支架重力不计)
(2)若A处螺钉的水平拉力最大为400 N,则在室外机位置不变的情况下,室外机重力不能超过多少牛
[方法指导] 利用杠杆的平衡条件分析和计算有关问题的一般步骤
(1)确定杠杆支点的位置.
(2)分析杠杆受到的动力和阻力,明确其大小和方向,并作出力的示意图.
(3)确定动力臂和阻力臂.
(4)根据杠杆的平衡条件列出关系式并分析求解.
【课堂小结】
答案
一、 杠 杆
【新知梳理】
一、1.力的作用下 固定点
2.转动 阻碍 动力作用线 阻力作用线
二、1.静止 匀速转动
2.(1)弹簧测力计 (3)①水平 ②竖直 水平
(6)动力×动力臂=阻力×阻力臂 F1l1=F2l2
(7)①杠杆自重 右 ②测量力臂 ③得出普遍规律,避免实验结论的偶然性 ④变大 动力臂
三、> < < > = =
【应用示例】
例1 如图所示
例2 (1)右 力臂 杠杆自重
(2)15 (3)能
(4)①对弹簧测力计进行调零 ②C C
(1)现在杠杆左端仍有轻微下沉,说明杠杆左端偏重,为使杠杆在水平位置平衡,应将右端的平衡螺母向右端调节,使杠杆在水平位置平衡,从而消除杠杆自重对实验的影响.(2)设一个钩码重为G,左边再加两个相同的钩码后,则左边力和力臂的乘积为F左l左=3G×20 cm,右边再加两个相同的钩码后,则右边力和力臂的乘积为F右l右=4G×l右,为了使杠杆在水平位置平衡,F左l左=F右l右,即3G×20 cm=4G×l右,所以l右=15 cm,他应将右端钩码移动到右端15 cm刻度线处.(3)杠杆的重心在支点处,将杠杆转过一个角度松手后,动力和阻力不变,动力臂和阻力臂的比值不变,仍符合F左l左=F右l右,杠杆仍然是平衡的,所以能保持静止.(4)①进行A、B两次实验时,弹簧测力计所施加的拉力的方向不同,所以图A操作后、图B操作前需要对弹簧测力计进行调零.②小明得到“动力×支点到动力作用点的距离=阻力×支点到阻力作用点的距离”,这个结论是不正确的;可在动力臂不等于支点到动力作用点的距离时,看实验结论是否成立,所以利用图C进行验证.三个图中钩码的重力及其位置均不变,图C中测力计拉力的力臂最小,所以需要用的拉力最大.
例3 A 筷子在使用过程中,动力臂小于阻力臂,是费力杠杆;瓶盖起子在使用过程中,动力臂大于阻力臂,是省力杠杆;撬棒在使用过程中,动力臂大于阻力臂,是省力杠杆;核桃夹在使用过程中,动力臂大于阻力臂,是省力杠杆.
例4 如图所示
例5 30 N 不变
例6 (1)由题知,阻力臂l2=AB=×40 cm=20 cm=0.2 m,动力臂l1=AC=30 cm=0.3 m,根据杠杆平衡条件,A处螺钉的水平拉力为
FA===200 N.
(2)若A处螺钉的水平拉力最大为400 N,根据杠杆平衡条件得,室外机的重力最大为
G'===600 N.
同课章节目录
- 第十一章 简单机械和功
- 1 杠杆
- 2 滑轮
- 3 功
- 4 功率
- 5 机械效率
- 第十二章 机械能和内能
- 1 动能 势能 机械能
- 2 内能 热传递
- 3 物质的比热容
- 4 机械能和内能的相互转化
- 第十三章 电路初探
- 1 初识家用电器和电路
- 2 电路连接的基本方式
- 3 电流和电流表的使用
- 4 电压和电压表的使用
- 第十四章 欧姆定律
- 1 电阻
- 2 变阻器
- 3 欧姆定律
- 4 欧姆定律的应用
- 第十五章 电功和电热
- 电能表与电功
- 电功率
- 电热器 电流的热效应
- 家庭电路与安全用电
- 第十六章 电磁转换
- 磁体与磁场
- 电流的磁场
- 磁场对电流的作用 电动机
- 安装直流电动机模型
- 电磁感应 发电机
- 第十七章 电磁波与现代通信
- 信息与信息传播
- 电磁波及其传播
- 现代通信 走进信息时代
- 第十八章 能源与可持续发展
- 能源利用与社会发展
- 核能
- 太阳能
- 能量转化的基本规律
- 能源与可持续发展
