高中数学人教新课标B版必修3--《2.1.2 系统抽样》 课件(共17张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修3--《2.1.2 系统抽样》 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
§2.1.2 系统抽样
(1)简单随机抽样
(2)我们所讨论的简单随机抽样都是不放回的抽样,即抽取到某个个体后,该个体不再放回总体中.常用到的简单随机抽样方法有两种: _________ 和_________.
一、复习回顾:
一般地,设一个总体的个体数为N,如果通过逐个不放回地抽取n个个体作为样本(n抽签法(抓阄法)
随机数法
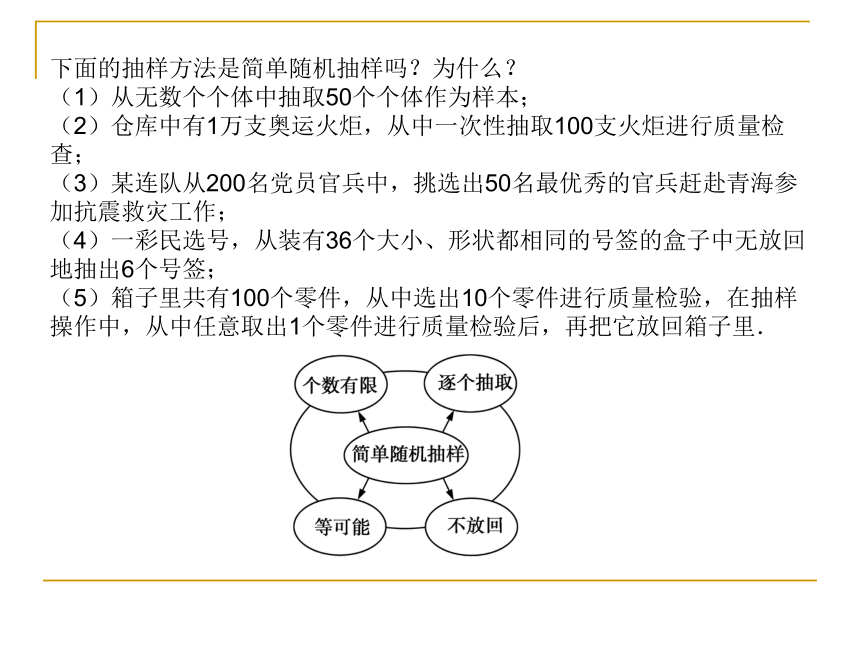
下面的抽样方法是简单随机抽样吗?为什么?
(1)从无数个个体中抽取50个个体作为样本;
(2)仓库中有1万支奥运火炬,从中一次性抽取100支火炬进行质量检查;
(3)某连队从200名党员官兵中,挑选出50名最优秀的官兵赶赴青海参加抗震救灾工作;
(4)一彩民选号,从装有36个大小、形状都相同的号签的盒子中无放回地抽出6个号签;
(5)箱子里共有100个零件,从中选出10个零件进行质量检验,在抽样操作中,从中任意取出1个零件进行质量检验后,再把它放回箱子里.
思考1:为了了解高一年级学生对老师教学的意见,教务处打算从年级500名学生中抽取50名进行问卷调查,那么年级每个同学被抽到的概率是多少?
思考2:你能用简单随机抽样对上述问题进行抽样吗?具体如何操作?
二、知识探究(一):简单随机抽样的基本思想
思考3:如果问题改为从5000人中抽取500名,简单的随机抽样好处理吗?
抽签法抽取样本的步骤:
随机数表法抽取样本的步骤:
编号;制签;搅匀;抽签;取个体。
编号;选数;读数;取个体。
那你能否设计其他抽样的方法?
思考4:如果从5000件产品中抽取500件进行质量检查,按照上述思路抽样应如何操作?
第二步,将总体平均分成500部分,每一部分含10个个体.
第四步,从该号码起,每隔10个号码取一个号码,就得到一个容量为500的样本.(如8,18,28,…,5998)
第三步,在第1部分中用简单随机抽样抽取一个号码(如8号).
第一步,将这5000件产品编号为1,2,3,…,5000.
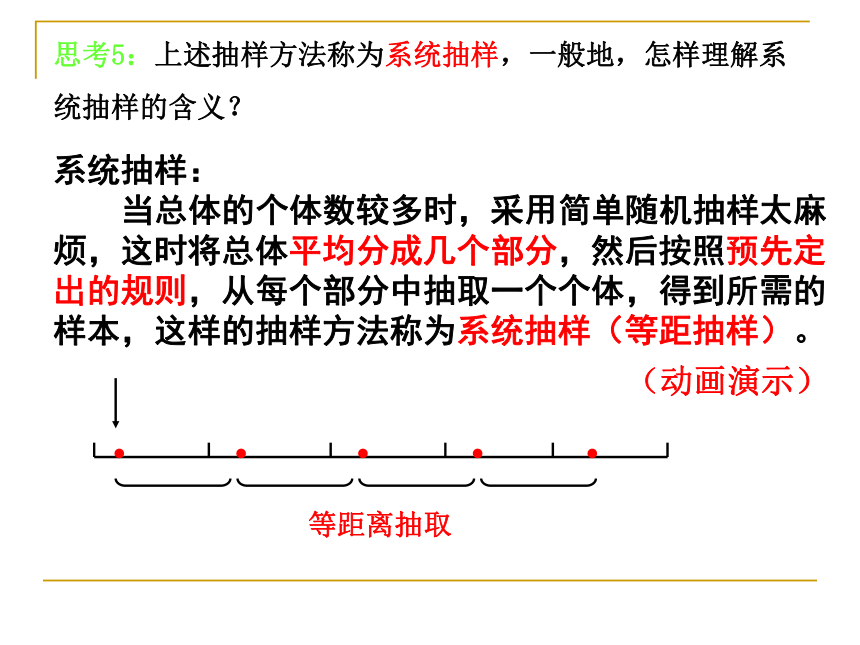
思考5:上述抽样方法称为系统抽样,一般地,怎样理解系统抽样的含义?
系统抽样:
当总体的个体数较多时,采用简单随机抽样太麻烦,这时将总体平均分成几个部分,然后按照预先定出的规则,从每个部分中抽取一个个体,得到所需的样本,这样的抽样方法称为系统抽样(等距抽样)。
等距离抽取
(动画演示)
思考1:用系统抽样从总体中抽取样本时,首先要做的工作是什么?
将总体中的所有个体编号.
先从总体中随机剔除5个个体,再均衡分成500部分.
知识探究(二):系统抽样的操作步骤
思考2:如果用系统抽样从5005件产品中抽取500件进行质量检查,由于5005件产品不能均衡分成500部分,对此应如何处理?
系统抽样的特点:
(1)用系统抽样抽取样本时,每个个体被抽到的可能性是相等的,
个体被抽取的概率等于
(2)系统抽样适用于总体中个体数较多,抽取样本容量也较大时;
(3)系统抽样是不放回抽样。
思考5:将含有N个个体的总体平均分成n段,每段的号码个数称为分段间隔,那么分段间隔k的值如何确定?
总体中的个体数N除以样本容量n所得的商.
思考6:用系统抽样抽取样本时,每段各取一个号码,其中第1段的个体编号怎样抽取?以后各段的个体编号怎样抽取?
用简单随机抽样抽取第1段的个体编号.在抽取第1段的号码之前,自定义规则确定以后各段的个体编号,通常是将第1段抽取的号码依次累加间隔k.
思考4:如果N不能被n整除怎么办?
从总体中随机剔除 N除以n的余数个个体后再分段.
思考3:用系统抽样从含有N个个体的总体中抽取一个容量为n的样本,要平均分成多少段,每段各有多少个号码?
(3)在第一段中用简单随机抽样确定起始的个体编号 ;
(4)将编号为 的个体抽出。
(2)将整个的编号按一定的间隔(设为K)分段,当 (N为总体中的个体数,n为样本容量)是整数时, ;当 不是整数时,从总体中剔除一些个体,使剩下的总体中个体的个数 能被n整除,这时, ,并将剩下的总体重新编号;
系统抽样的步骤:
简记为:编号;分段;在第一段确定起始号;加间隔获取样本。
(1)采用随机的方式将总体中的个体编号;
学号、准考证号、身份证号
思考7:一般地,用系统抽样从含有N个个体的总体中抽取一个容量为n的样本,其操作步骤如何?
思考8:系统抽样与简单随机抽样比较,有何区别及共同点?
简单随机抽样 系统抽样
区别 ①操作简单易行;②抽样的结果与个体编号无关 ①当总体中的个体数较大时,用系统抽样更易实施,更节约成本;②系统抽样的效果与个体的编号有关,如果编号的特征随编号呈周期性变化,可能使样本的代表性很差
联系 系统抽样在总体中的个体均匀分段后,在第一段进行抽样时,采用的是简单随机抽样
例1(1)下列问题中,最适合用系统抽样抽取样本的是( )
A.从10名学生中,随机抽2名学生参加义务劳动
B.从全校3 000名学生中,随机抽100名学生参加义务劳动
C.从某市30 000名学生中,其中小学生有14 000人,初中生有10 000人,高中生有6 000人,抽取300名学生了解该市学生的近视情况
D.从某班周二值日小组6人中,随机抽取1人擦黑板
(2)下列抽样方法不是系统抽样的是( )
A.从标有1~15号的15个球中,任选三个作样本,按从小号到大号的顺序,随机选起点i0,以后选i0+5,i0+10(超过15则从1再数起)号入选
B.工厂生产的产品用传送带将产品送入包装车间前,在一天时间内检验人员从传送带上每隔五分钟抽一件产品进行检验
C.做某项市场调查,规定在商场门口随机抽一个人进行询问调查,直到达到事先规定的调查人数为止
D.电影院调查观众的某一指标,通知每排(每排人数相等)座位号为14的观众留下来座谈
B
C
三、典例分析
例2(1)某中学有高一学生322名,为了了解学生的身体状况,要抽取一个容量为40的样本,用系统抽样法如何抽样?
解:第一步,随机剔除2名学生,把余下的320名学生编号为1,2,3,…320.
第四步,从该号码起,每间隔8个号码抽取1个号码,就可得到一个容量为40的样本.
第三步,在第1部分用抽签法确定起始编号.
第二步,把总体分成40个部分,每个部分有8个个体.
(2)请合理选择抽样方法进行抽样,并说明抽样过程
从某厂生产的703件产品中随机抽取70件测试某项指标;
从某厂生产的703件产品中随机抽取7件测试某项指标;
从某厂生产的30件产品中随机抽取4件测试某项指标.
2、采用系统抽样的方法,从个体数为1003的总体中抽取一个容量50的样本,则在抽样过程中,被剔除的个体数( ),抽样间隔为( )。
3
20
四、课堂练习:
1、某工厂生产产品,用传送带将产品送放下一道工序,质检人员每隔十分钟在传送带的某一个位置取一件检验,则这种抽样方法是( )。
A.抽签法 B.随机数表法 C.系统抽样 D.其他
C
3.将参加数学竞赛的1000名学生编号如下000,001,002,…,999,打算从中抽取一个容量为50的样本,按系统抽样方法分成50个部分,第一组编号000,001,…,019,如果在第一组随机抽取的号码为015,则第30个号码为________.
595
4、用系统抽样的方法从个体数为1003的总体中抽取一个容量为50的样本,在整个抽样过程中每个个体被抽到的可能性为( )
A、1/1000 B、1/1003 C、50/1003 D、50/1000
5、从N个编号中抽取n个号码入样,用系统的方法抽样,则抽样的间隔为( )
A、N/n B、n C、[N/n] D、[N/n]+1
说明:[N/n]表示N/n的整数部分。
6、从已编号为1-50的50枚最新研制的某种型号的导弹中随机抽取5枚来进行发射实验,若采用每部分选取的号码间隔一样的系统抽样方法,则所选取5枚导弹的编号可能为( )
A、5,10,15,20,25 B、3,13,23,33,43
C、1,2,3,4,5 D、2,4,6,16,32
C
C
B
2.系统抽样适合于总体的个体数较多的情形,操作上分四个步骤进行,除了剔除余数个体和确定起始号需要随机抽样外,其余样本号码由事先定下的规则自动生成,从而使得系统抽样操作简单、方便.
1.系统抽样也是等概率抽样,即每个个体被抽到的概率是相等的,从而保证了抽样的公平性.
五、课堂小结
7.将参加夏令营的600名学生编号为:001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为004,这600名学生分住在三个营区.从001到300在第Ⅰ营区,从301到495在第Ⅱ营区,从496到600在第Ⅲ营区.三个营区被抽中的人数依次为( )
A. 24,17,9 B.25,16,9 C. 25,17,8 D. 26,16,8
B
抽样方法
简单随机抽样 抽签法
系统抽样
随机数表法
共同点 (1)抽样过程中每个个体被抽到的概率相等;(2)都要先编号
各自特点 从总体中逐一抽取 先均分,再按事先确定的规则在各部分抽取
相互联系 在起始部分抽样时采用简单随机抽样
适用范围 总体中的个体数较少 总体中的个体数较多
两种抽样方法比较
返回
§2.1.2 系统抽样
(1)简单随机抽样
(2)我们所讨论的简单随机抽样都是不放回的抽样,即抽取到某个个体后,该个体不再放回总体中.常用到的简单随机抽样方法有两种: _________ 和_________.
一、复习回顾:
一般地,设一个总体的个体数为N,如果通过逐个不放回地抽取n个个体作为样本(n
随机数法
下面的抽样方法是简单随机抽样吗?为什么?
(1)从无数个个体中抽取50个个体作为样本;
(2)仓库中有1万支奥运火炬,从中一次性抽取100支火炬进行质量检查;
(3)某连队从200名党员官兵中,挑选出50名最优秀的官兵赶赴青海参加抗震救灾工作;
(4)一彩民选号,从装有36个大小、形状都相同的号签的盒子中无放回地抽出6个号签;
(5)箱子里共有100个零件,从中选出10个零件进行质量检验,在抽样操作中,从中任意取出1个零件进行质量检验后,再把它放回箱子里.
思考1:为了了解高一年级学生对老师教学的意见,教务处打算从年级500名学生中抽取50名进行问卷调查,那么年级每个同学被抽到的概率是多少?
思考2:你能用简单随机抽样对上述问题进行抽样吗?具体如何操作?
二、知识探究(一):简单随机抽样的基本思想
思考3:如果问题改为从5000人中抽取500名,简单的随机抽样好处理吗?
抽签法抽取样本的步骤:
随机数表法抽取样本的步骤:
编号;制签;搅匀;抽签;取个体。
编号;选数;读数;取个体。
那你能否设计其他抽样的方法?
思考4:如果从5000件产品中抽取500件进行质量检查,按照上述思路抽样应如何操作?
第二步,将总体平均分成500部分,每一部分含10个个体.
第四步,从该号码起,每隔10个号码取一个号码,就得到一个容量为500的样本.(如8,18,28,…,5998)
第三步,在第1部分中用简单随机抽样抽取一个号码(如8号).
第一步,将这5000件产品编号为1,2,3,…,5000.
思考5:上述抽样方法称为系统抽样,一般地,怎样理解系统抽样的含义?
系统抽样:
当总体的个体数较多时,采用简单随机抽样太麻烦,这时将总体平均分成几个部分,然后按照预先定出的规则,从每个部分中抽取一个个体,得到所需的样本,这样的抽样方法称为系统抽样(等距抽样)。
等距离抽取
(动画演示)
思考1:用系统抽样从总体中抽取样本时,首先要做的工作是什么?
将总体中的所有个体编号.
先从总体中随机剔除5个个体,再均衡分成500部分.
知识探究(二):系统抽样的操作步骤
思考2:如果用系统抽样从5005件产品中抽取500件进行质量检查,由于5005件产品不能均衡分成500部分,对此应如何处理?
系统抽样的特点:
(1)用系统抽样抽取样本时,每个个体被抽到的可能性是相等的,
个体被抽取的概率等于
(2)系统抽样适用于总体中个体数较多,抽取样本容量也较大时;
(3)系统抽样是不放回抽样。
思考5:将含有N个个体的总体平均分成n段,每段的号码个数称为分段间隔,那么分段间隔k的值如何确定?
总体中的个体数N除以样本容量n所得的商.
思考6:用系统抽样抽取样本时,每段各取一个号码,其中第1段的个体编号怎样抽取?以后各段的个体编号怎样抽取?
用简单随机抽样抽取第1段的个体编号.在抽取第1段的号码之前,自定义规则确定以后各段的个体编号,通常是将第1段抽取的号码依次累加间隔k.
思考4:如果N不能被n整除怎么办?
从总体中随机剔除 N除以n的余数个个体后再分段.
思考3:用系统抽样从含有N个个体的总体中抽取一个容量为n的样本,要平均分成多少段,每段各有多少个号码?
(3)在第一段中用简单随机抽样确定起始的个体编号 ;
(4)将编号为 的个体抽出。
(2)将整个的编号按一定的间隔(设为K)分段,当 (N为总体中的个体数,n为样本容量)是整数时, ;当 不是整数时,从总体中剔除一些个体,使剩下的总体中个体的个数 能被n整除,这时, ,并将剩下的总体重新编号;
系统抽样的步骤:
简记为:编号;分段;在第一段确定起始号;加间隔获取样本。
(1)采用随机的方式将总体中的个体编号;
学号、准考证号、身份证号
思考7:一般地,用系统抽样从含有N个个体的总体中抽取一个容量为n的样本,其操作步骤如何?
思考8:系统抽样与简单随机抽样比较,有何区别及共同点?
简单随机抽样 系统抽样
区别 ①操作简单易行;②抽样的结果与个体编号无关 ①当总体中的个体数较大时,用系统抽样更易实施,更节约成本;②系统抽样的效果与个体的编号有关,如果编号的特征随编号呈周期性变化,可能使样本的代表性很差
联系 系统抽样在总体中的个体均匀分段后,在第一段进行抽样时,采用的是简单随机抽样
例1(1)下列问题中,最适合用系统抽样抽取样本的是( )
A.从10名学生中,随机抽2名学生参加义务劳动
B.从全校3 000名学生中,随机抽100名学生参加义务劳动
C.从某市30 000名学生中,其中小学生有14 000人,初中生有10 000人,高中生有6 000人,抽取300名学生了解该市学生的近视情况
D.从某班周二值日小组6人中,随机抽取1人擦黑板
(2)下列抽样方法不是系统抽样的是( )
A.从标有1~15号的15个球中,任选三个作样本,按从小号到大号的顺序,随机选起点i0,以后选i0+5,i0+10(超过15则从1再数起)号入选
B.工厂生产的产品用传送带将产品送入包装车间前,在一天时间内检验人员从传送带上每隔五分钟抽一件产品进行检验
C.做某项市场调查,规定在商场门口随机抽一个人进行询问调查,直到达到事先规定的调查人数为止
D.电影院调查观众的某一指标,通知每排(每排人数相等)座位号为14的观众留下来座谈
B
C
三、典例分析
例2(1)某中学有高一学生322名,为了了解学生的身体状况,要抽取一个容量为40的样本,用系统抽样法如何抽样?
解:第一步,随机剔除2名学生,把余下的320名学生编号为1,2,3,…320.
第四步,从该号码起,每间隔8个号码抽取1个号码,就可得到一个容量为40的样本.
第三步,在第1部分用抽签法确定起始编号.
第二步,把总体分成40个部分,每个部分有8个个体.
(2)请合理选择抽样方法进行抽样,并说明抽样过程
从某厂生产的703件产品中随机抽取70件测试某项指标;
从某厂生产的703件产品中随机抽取7件测试某项指标;
从某厂生产的30件产品中随机抽取4件测试某项指标.
2、采用系统抽样的方法,从个体数为1003的总体中抽取一个容量50的样本,则在抽样过程中,被剔除的个体数( ),抽样间隔为( )。
3
20
四、课堂练习:
1、某工厂生产产品,用传送带将产品送放下一道工序,质检人员每隔十分钟在传送带的某一个位置取一件检验,则这种抽样方法是( )。
A.抽签法 B.随机数表法 C.系统抽样 D.其他
C
3.将参加数学竞赛的1000名学生编号如下000,001,002,…,999,打算从中抽取一个容量为50的样本,按系统抽样方法分成50个部分,第一组编号000,001,…,019,如果在第一组随机抽取的号码为015,则第30个号码为________.
595
4、用系统抽样的方法从个体数为1003的总体中抽取一个容量为50的样本,在整个抽样过程中每个个体被抽到的可能性为( )
A、1/1000 B、1/1003 C、50/1003 D、50/1000
5、从N个编号中抽取n个号码入样,用系统的方法抽样,则抽样的间隔为( )
A、N/n B、n C、[N/n] D、[N/n]+1
说明:[N/n]表示N/n的整数部分。
6、从已编号为1-50的50枚最新研制的某种型号的导弹中随机抽取5枚来进行发射实验,若采用每部分选取的号码间隔一样的系统抽样方法,则所选取5枚导弹的编号可能为( )
A、5,10,15,20,25 B、3,13,23,33,43
C、1,2,3,4,5 D、2,4,6,16,32
C
C
B
2.系统抽样适合于总体的个体数较多的情形,操作上分四个步骤进行,除了剔除余数个体和确定起始号需要随机抽样外,其余样本号码由事先定下的规则自动生成,从而使得系统抽样操作简单、方便.
1.系统抽样也是等概率抽样,即每个个体被抽到的概率是相等的,从而保证了抽样的公平性.
五、课堂小结
7.将参加夏令营的600名学生编号为:001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为004,这600名学生分住在三个营区.从001到300在第Ⅰ营区,从301到495在第Ⅱ营区,从496到600在第Ⅲ营区.三个营区被抽中的人数依次为( )
A. 24,17,9 B.25,16,9 C. 25,17,8 D. 26,16,8
B
抽样方法
简单随机抽样 抽签法
系统抽样
随机数表法
共同点 (1)抽样过程中每个个体被抽到的概率相等;(2)都要先编号
各自特点 从总体中逐一抽取 先均分,再按事先确定的规则在各部分抽取
相互联系 在起始部分抽样时采用简单随机抽样
适用范围 总体中的个体数较少 总体中的个体数较多
两种抽样方法比较
返回
