高中数学人教新课标B版必修3--《2.3.2 两个变量的线性相关》 课件(共26张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修3--《2.3.2 两个变量的线性相关》 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 14:22:05 | ||
图片预览




文档简介
(共26张PPT)
2.3.2两个变量的线性相关
人民教育出版社B版必修3
探究新知
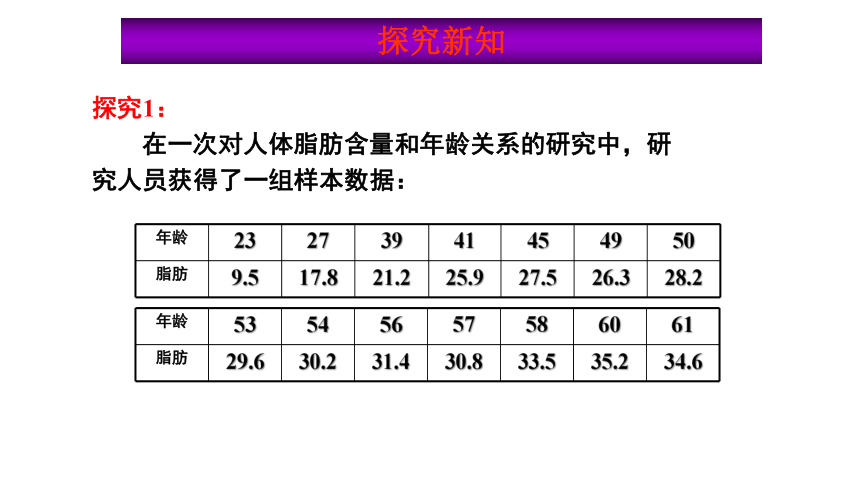
探究1:
在一次对人体脂肪含量和年龄关系的研究中,研
究人员获得了一组样本数据:
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
探究新知
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
探究新知
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
探究新知
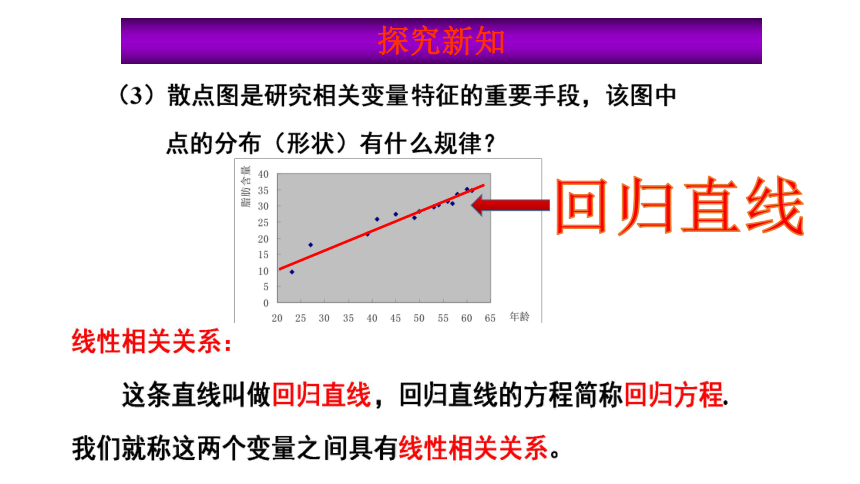
该图叫做
散点图.
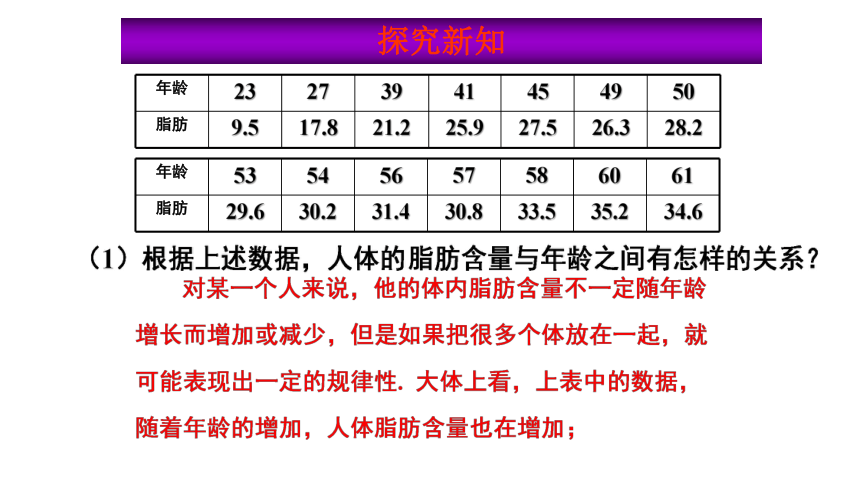
从散点图可以看出,年龄越大,体内脂肪含量越高.
探究新知
探究新知
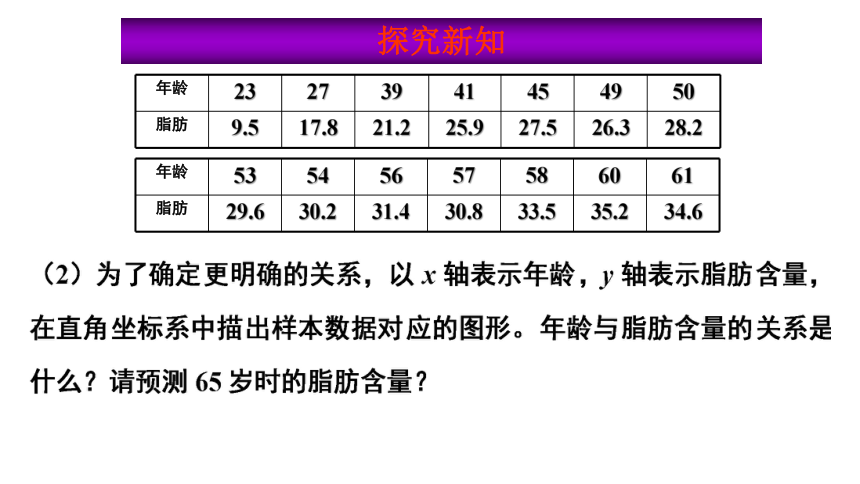
探究2:
只有散点图中的点呈条状集中在某一直线周围,
才可以用回归直线来描述两个变量之间的关系. 如何确定出这条直线的位置呢?
探究新知
如果要在下面5个城市间建一条高速公路(直路)以方便从这条高速公路到各个城市,你认为该怎么建?
整体:5个城市到直路的距离和最短
创设情景 挖掘内涵
探究3:设回归直线方程是y=bx+a,如何从代数角度刻画“从整体上看,各点到此直线的整体距离最小?
对一组具有线性相关的两个变量的样本数据:
(x1, y1)
(x2,y2)
(xn,yn)
(xi,yi)
o
x
y
“从整体上看,各点与直线的距离最小”
“整体距离”最小
各点到直线的距离和最小
深入探究 挖掘内涵
(x1,y1)
(x2,y2)
(xn,yn)
模型一:
深入探究 挖掘内涵
(x1,y1)
(x2,y2)
(xn,yn)
模型一:求 最小值
模型二:求 最小值
深入探究 挖掘内涵
类比方差和标准差
各点与直线
的整体距离
深入探究 挖掘内涵
问题归结为:a,b取什么值时Q最小,即总体和最小.
Q = (y1-bx1-a)2 + (y2-bx2-a)2 +…+ (yn-bxn-a)2
探究最小二乘法
先对a配方
探究最小二乘法
再对b 配方
探究最小二乘法
这种通过求:
的最小值而得到回归直线的方法,即求样本数据的点到
回归直线的距离的平方和最小的方法叫做最小二乘法.
探究最小二乘法
4、回归方程的系数公式:
回归方程 ,其中:
回归方程
模型应用
解:(1)散点图如图示:
模型应用
(2)由题意得:
回归方程为:
模型应用
(3)由回归方程预测,
即四家企业销售额约为34.1(百亿元).
模型应用
.
归纳:
求回归方程 的步骤:
小结
拓展训练
拓展训练
(1)散点图:
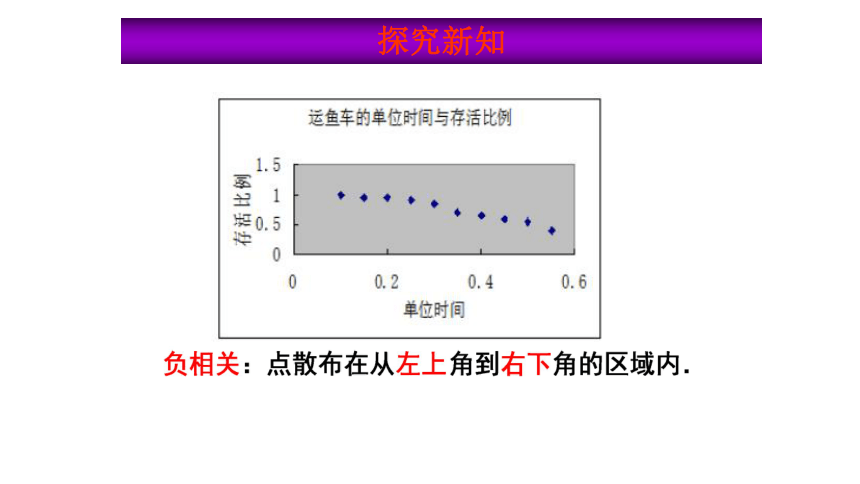
(2)正相关、负相关:
(3)线性相关关系:
(4)回归方程的系数公式:
1、知识:
(1)最小二乘法:
(2)转化与化归;
数形结合;统计思想
2、思想方法:
事件
回归方程
样本数据
预测
抽样
决定
总结升华
2.3.2两个变量的线性相关
人民教育出版社B版必修3
探究新知
探究1:
在一次对人体脂肪含量和年龄关系的研究中,研
究人员获得了一组样本数据:
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
探究新知
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
探究新知
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
探究新知
该图叫做
散点图.
从散点图可以看出,年龄越大,体内脂肪含量越高.
探究新知
探究新知
探究2:
只有散点图中的点呈条状集中在某一直线周围,
才可以用回归直线来描述两个变量之间的关系. 如何确定出这条直线的位置呢?
探究新知
如果要在下面5个城市间建一条高速公路(直路)以方便从这条高速公路到各个城市,你认为该怎么建?
整体:5个城市到直路的距离和最短
创设情景 挖掘内涵
探究3:设回归直线方程是y=bx+a,如何从代数角度刻画“从整体上看,各点到此直线的整体距离最小?
对一组具有线性相关的两个变量的样本数据:
(x1, y1)
(x2,y2)
(xn,yn)
(xi,yi)
o
x
y
“从整体上看,各点与直线的距离最小”
“整体距离”最小
各点到直线的距离和最小
深入探究 挖掘内涵
(x1,y1)
(x2,y2)
(xn,yn)
模型一:
深入探究 挖掘内涵
(x1,y1)
(x2,y2)
(xn,yn)
模型一:求 最小值
模型二:求 最小值
深入探究 挖掘内涵
类比方差和标准差
各点与直线
的整体距离
深入探究 挖掘内涵
问题归结为:a,b取什么值时Q最小,即总体和最小.
Q = (y1-bx1-a)2 + (y2-bx2-a)2 +…+ (yn-bxn-a)2
探究最小二乘法
先对a配方
探究最小二乘法
再对b 配方
探究最小二乘法
这种通过求:
的最小值而得到回归直线的方法,即求样本数据的点到
回归直线的距离的平方和最小的方法叫做最小二乘法.
探究最小二乘法
4、回归方程的系数公式:
回归方程 ,其中:
回归方程
模型应用
解:(1)散点图如图示:
模型应用
(2)由题意得:
回归方程为:
模型应用
(3)由回归方程预测,
即四家企业销售额约为34.1(百亿元).
模型应用
.
归纳:
求回归方程 的步骤:
小结
拓展训练
拓展训练
(1)散点图:
(2)正相关、负相关:
(3)线性相关关系:
(4)回归方程的系数公式:
1、知识:
(1)最小二乘法:
(2)转化与化归;
数形结合;统计思想
2、思想方法:
事件
回归方程
样本数据
预测
抽样
决定
总结升华
