高中数学人教新课标B版必修3--《3.1.2 事件与基本事件空间》 课件(共30张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修3--《3.1.2 事件与基本事件空间》 课件(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
问题1:这个游戏规则公平吗?小组讨论.
每位同学可以伸出1~5根手指,同桌俩人像玩剪刀、石头、布一样伸出自己的手指数,记下自己的数字.
游戏规则是:将两人的数字相加,和为5算坐在左边的同学赢,和不为5算右边的同学赢.游戏结束后,统计输赢情况.
问题2:两人出手指,所有可能的结果究竟有哪些?“和为5”包含了哪些结果 “和不为5”又包含了哪些结果呢?
我们来做个游戏
试验1:
郭艾伦在某次比赛第一小节共投篮5次,那么:
结果1:“投进6次”
结果2:“投进次数小于6”
结果3:“投进4次”
探究一
试验2:
10个相同的小球,其中8个绿球,2个红球,从中任意抽出3个小球,观察出现的红色小球的个数.
结果1:“抽到3个红球”
结果2:“至少抽到1个绿球”
结果3:“抽到2个绿球,1个红球”
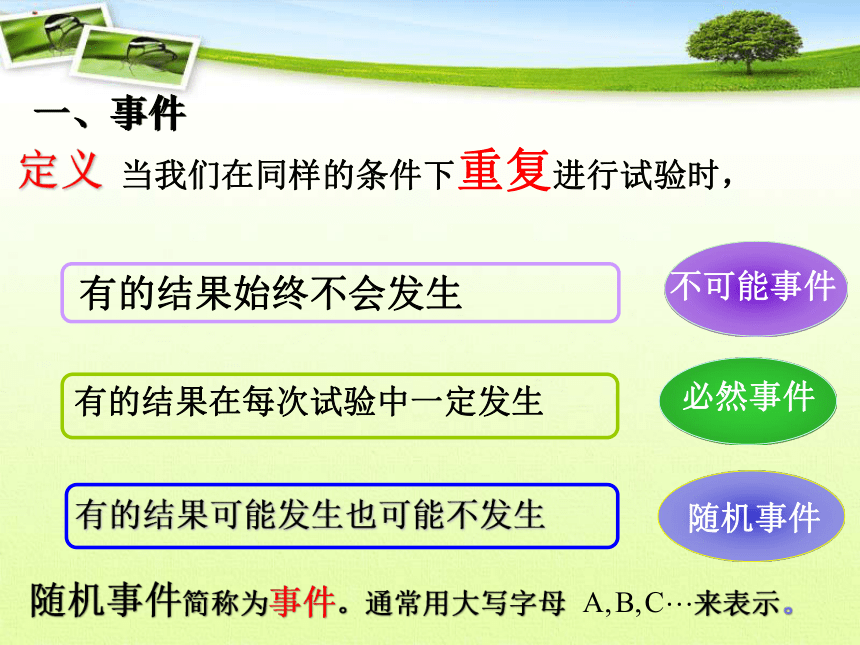
一、事件
随机事件
必然事件
不可能事件
有的结果可能发生也可能不发生
有的结果在每次试验中一定发生
有的结果始终不会发生
当我们在同样的条件下重复进行试验时,
定义
随机事件简称为事件。通常用大写字母 来表示。
1.在标准大气压下,温度低于0℃时,冰融化;
2.在常温下,铁块熔化;
3.掷一枚硬币,出现正面;
4.2017年6月7日沈阳下雨;
5.如果a>b,那么a-b>0;
6.导体通电后发热;
7.函数 在其定义域内是增函数.
8.在整数范围内,方程x2-2=0有解.
不可能事件
不可能事件
随机事件
随机事件
必然事件
必然事件
随机事件
不可能事件
下列事件中,哪些是必然事件?哪些是不可能事件?哪些是随机事件?
试验1:掷一枚硬币,观察硬币落地后哪一面朝上.
观察下列试验,每一个试验可能出现的结果都有哪些?
试验2:掷一颗骰子,观察掷出的点数.
以上这些结果都是试验中不能再分的最简单的随机事件
探究二
正面向上,反面向上
1,2,3,4,5,6
二、基本事件与基本事件空间
在一次试验中,不能再分解的最简单的随机事件,其他事件可以用它们来描绘,这样的事件
称为基本事件。
基本事件
所有基本事件构成的集合称为基本事件空间,
用 表示
基本事件空间
试验1:掷一枚硬币,观察硬币落地后哪一面朝上.
试验2:掷一颗骰子,观察掷出的点数.
事件A=“出现奇数点”
事件B=“点数大于3”
我们在哪里学过这种表示呢?
※事件、基本事件和基本事件空间的关系:
基本事件空间
事件A
●
●
●
●
●
基本事件
一个事件可以由若干个基本事件组成,
即随机事件可以理解为基本事件空间的子集。
基本事件可以理解为基本事件空间中不能再分的最小元素
例1.一先一后掷两枚硬币,观察正面向上的情况,
(1)写出基本事件空间;
(2)“一正一反”这个事件的含义;
(3)“至少有一次出现正面”这个事件包含哪几个基本事件。
变式:连续掷 3枚 硬币,观察落地后这3枚硬币的正反面情况.写出这个试验的基本事件空间;
?探讨:怎样才能准确的写出全部基本事件,并保证不重不漏呢?
4枚
方法1 在两枚的基础上增加第三枚硬币出现的结果
={(正,正,正),(正,正,反),
(反,反,正),(反,反,反),
(正,反,正),(正,反,反),
(反,正,正),(反,正,反)}.
变式:连续掷3枚硬币,观察落地后这3枚硬币的正反面情况.写出这个试验的基本事件空间;
方法2 按照正面向上的次数的多少进行分类,
分为有3次为正,有2次为正,有1次为正,有0次为正
={(正,正,正),
变式:连续掷3枚硬币,观察落地后这3枚硬币的正反面情况.写出这个试验的基本事件空间;
(正,正,反),(正,反,正),(反,正,正),
(正,反,反),(反,正,反),(反,反,正),
(反,反,反)}.
方法3 用树状图表示.
变式:连续掷3枚硬币,观察落地后这3枚硬币的正反面情况.写出这个试验的基本事件空间;
第一行是第一次掷的结果,第二行是第二次掷的结果,
第三行是第三次掷的结果.
正
反
正
反
正
正
反
反
正
反
正
正
反
反
例2:做投掷2颗骰子的试验,用(x,y)表示结果,其中x表示第一颗骰子出现的点数,y表示第2颗骰子出现的点数.写出
(1)基本事件空间,包含的基本事件个数;
(2)事件A“出现的点数相等”;
(3)事件B“出现的点数之和等于8”;
(4)事件C“出现的点数之和大于10”;
树状图表示
1
1
2
3
6
5
4
2
1
2
3
6
5
4
3
1
2
3
6
5
4
4
1
2
3
6
5
4
5
1
2
3
6
5
4
6
1
2
3
6
5
4
(1)基本事件空间为
共包含36个基本事件
1 2 3 4 5 6
1 (1,1) (2,1) (3,1) (4,1) (5,1) (6,1)
2 (1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
3 (1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
4 (1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
5 (1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
6 (1,6) (2,6) (3,6) (4,6) (5,6) (6,6)
列表格表示
x
y
(2)事件A“出现点数相等”
1 2 3 4 5 6
1
2
3
4
5
6
y
x
点阵表示
7 8 9 10 11 12
6 7 8 9 10 11
5 6 7 8 9 10
4 5 6 7 8 9
2 3 4 5 6 7
3 4 5 6 7 8
(3)事件B“出现的点数之和等于8”;
(4)事件C“出现的点数之和大于10”;
问题1:这个游戏规则公平吗?小组讨论.
每位同学可以伸出1~5根手指,同桌俩人像玩剪刀、石头、布一样伸出自己的手指数,记下自己的数字.
游戏规则是:将两人的数字相加,和为5算坐在左边的同学赢,和不为5算右边的同学赢.游戏结束后,统计输赢情况.
问题2:两人出手指,所有可能的结果究竟有哪些?“和为5”包含了哪些结果 “和不为5”又包含了哪些结果呢?
我们来做个游戏
例3 从A、B、C、D、E、F共6名学生中选出4人参加数学竞赛,
(1)写出这个试验的基本事件空间;
(2)求这个试验的基本事件总数;
(3)写出事件“A没被选中”所包含的基本事件’。
解:(1)这个试验的基本事件空间是:Ω={(A,B,C,D),(A,B,C,E),(A,B,C,F),(A,B,D,E),(A,B,D,F),(A,B,E,F),(A,C, D,E),(A,C,D,F),(A,C,E,F),(A,D,E,F),(B,C,D,E),(B,C,D,F),(B,C,E,F),(B,D,E, F),(C,D,E,F)};
(2)从6名学生中选出4人参加数学竞赛,共有15种可能情况;
(3)“A没被选中”包含下列5个基本事件:{(B,C,D,E),(B,C,D,F),(B,C,E,F),(B,D,E,F),(C,D,E,F)}。
随机
不可能
必然
A
取样方法的不同,基本事件空间有何区别?
袋中有红、白、黄、黑四个颜色不同、大小相同的球,
按下列要求分别进行试验:分别写出上面试验的基本
事件空间,并指出基本事件总数.
(1) 从中任取两个球;
(2)先取一球,取出后不放回,再取一球.
(3)先取一球,取出后放回,再取一球.
问题1:这个游戏规则公平吗?小组讨论.
每位同学可以伸出1~5根手指,同桌俩人像玩剪刀、石头、布一样伸出自己的手指数,记下自己的数字.
游戏规则是:将两人的数字相加,和为5算坐在左边的同学赢,和不为5算右边的同学赢.游戏结束后,统计输赢情况.
问题2:两人出手指,所有可能的结果究竟有哪些?“和为5”包含了哪些结果 “和不为5”又包含了哪些结果呢?
我们来做个游戏
试验1:
郭艾伦在某次比赛第一小节共投篮5次,那么:
结果1:“投进6次”
结果2:“投进次数小于6”
结果3:“投进4次”
探究一
试验2:
10个相同的小球,其中8个绿球,2个红球,从中任意抽出3个小球,观察出现的红色小球的个数.
结果1:“抽到3个红球”
结果2:“至少抽到1个绿球”
结果3:“抽到2个绿球,1个红球”
一、事件
随机事件
必然事件
不可能事件
有的结果可能发生也可能不发生
有的结果在每次试验中一定发生
有的结果始终不会发生
当我们在同样的条件下重复进行试验时,
定义
随机事件简称为事件。通常用大写字母 来表示。
1.在标准大气压下,温度低于0℃时,冰融化;
2.在常温下,铁块熔化;
3.掷一枚硬币,出现正面;
4.2017年6月7日沈阳下雨;
5.如果a>b,那么a-b>0;
6.导体通电后发热;
7.函数 在其定义域内是增函数.
8.在整数范围内,方程x2-2=0有解.
不可能事件
不可能事件
随机事件
随机事件
必然事件
必然事件
随机事件
不可能事件
下列事件中,哪些是必然事件?哪些是不可能事件?哪些是随机事件?
试验1:掷一枚硬币,观察硬币落地后哪一面朝上.
观察下列试验,每一个试验可能出现的结果都有哪些?
试验2:掷一颗骰子,观察掷出的点数.
以上这些结果都是试验中不能再分的最简单的随机事件
探究二
正面向上,反面向上
1,2,3,4,5,6
二、基本事件与基本事件空间
在一次试验中,不能再分解的最简单的随机事件,其他事件可以用它们来描绘,这样的事件
称为基本事件。
基本事件
所有基本事件构成的集合称为基本事件空间,
用 表示
基本事件空间
试验1:掷一枚硬币,观察硬币落地后哪一面朝上.
试验2:掷一颗骰子,观察掷出的点数.
事件A=“出现奇数点”
事件B=“点数大于3”
我们在哪里学过这种表示呢?
※事件、基本事件和基本事件空间的关系:
基本事件空间
事件A
●
●
●
●
●
基本事件
一个事件可以由若干个基本事件组成,
即随机事件可以理解为基本事件空间的子集。
基本事件可以理解为基本事件空间中不能再分的最小元素
例1.一先一后掷两枚硬币,观察正面向上的情况,
(1)写出基本事件空间;
(2)“一正一反”这个事件的含义;
(3)“至少有一次出现正面”这个事件包含哪几个基本事件。
变式:连续掷 3枚 硬币,观察落地后这3枚硬币的正反面情况.写出这个试验的基本事件空间;
?探讨:怎样才能准确的写出全部基本事件,并保证不重不漏呢?
4枚
方法1 在两枚的基础上增加第三枚硬币出现的结果
={(正,正,正),(正,正,反),
(反,反,正),(反,反,反),
(正,反,正),(正,反,反),
(反,正,正),(反,正,反)}.
变式:连续掷3枚硬币,观察落地后这3枚硬币的正反面情况.写出这个试验的基本事件空间;
方法2 按照正面向上的次数的多少进行分类,
分为有3次为正,有2次为正,有1次为正,有0次为正
={(正,正,正),
变式:连续掷3枚硬币,观察落地后这3枚硬币的正反面情况.写出这个试验的基本事件空间;
(正,正,反),(正,反,正),(反,正,正),
(正,反,反),(反,正,反),(反,反,正),
(反,反,反)}.
方法3 用树状图表示.
变式:连续掷3枚硬币,观察落地后这3枚硬币的正反面情况.写出这个试验的基本事件空间;
第一行是第一次掷的结果,第二行是第二次掷的结果,
第三行是第三次掷的结果.
正
反
正
反
正
正
反
反
正
反
正
正
反
反
例2:做投掷2颗骰子的试验,用(x,y)表示结果,其中x表示第一颗骰子出现的点数,y表示第2颗骰子出现的点数.写出
(1)基本事件空间,包含的基本事件个数;
(2)事件A“出现的点数相等”;
(3)事件B“出现的点数之和等于8”;
(4)事件C“出现的点数之和大于10”;
树状图表示
1
1
2
3
6
5
4
2
1
2
3
6
5
4
3
1
2
3
6
5
4
4
1
2
3
6
5
4
5
1
2
3
6
5
4
6
1
2
3
6
5
4
(1)基本事件空间为
共包含36个基本事件
1 2 3 4 5 6
1 (1,1) (2,1) (3,1) (4,1) (5,1) (6,1)
2 (1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
3 (1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
4 (1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
5 (1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
6 (1,6) (2,6) (3,6) (4,6) (5,6) (6,6)
列表格表示
x
y
(2)事件A“出现点数相等”
1 2 3 4 5 6
1
2
3
4
5
6
y
x
点阵表示
7 8 9 10 11 12
6 7 8 9 10 11
5 6 7 8 9 10
4 5 6 7 8 9
2 3 4 5 6 7
3 4 5 6 7 8
(3)事件B“出现的点数之和等于8”;
(4)事件C“出现的点数之和大于10”;
问题1:这个游戏规则公平吗?小组讨论.
每位同学可以伸出1~5根手指,同桌俩人像玩剪刀、石头、布一样伸出自己的手指数,记下自己的数字.
游戏规则是:将两人的数字相加,和为5算坐在左边的同学赢,和不为5算右边的同学赢.游戏结束后,统计输赢情况.
问题2:两人出手指,所有可能的结果究竟有哪些?“和为5”包含了哪些结果 “和不为5”又包含了哪些结果呢?
我们来做个游戏
例3 从A、B、C、D、E、F共6名学生中选出4人参加数学竞赛,
(1)写出这个试验的基本事件空间;
(2)求这个试验的基本事件总数;
(3)写出事件“A没被选中”所包含的基本事件’。
解:(1)这个试验的基本事件空间是:Ω={(A,B,C,D),(A,B,C,E),(A,B,C,F),(A,B,D,E),(A,B,D,F),(A,B,E,F),(A,C, D,E),(A,C,D,F),(A,C,E,F),(A,D,E,F),(B,C,D,E),(B,C,D,F),(B,C,E,F),(B,D,E, F),(C,D,E,F)};
(2)从6名学生中选出4人参加数学竞赛,共有15种可能情况;
(3)“A没被选中”包含下列5个基本事件:{(B,C,D,E),(B,C,D,F),(B,C,E,F),(B,D,E,F),(C,D,E,F)}。
随机
不可能
必然
A
取样方法的不同,基本事件空间有何区别?
袋中有红、白、黄、黑四个颜色不同、大小相同的球,
按下列要求分别进行试验:分别写出上面试验的基本
事件空间,并指出基本事件总数.
(1) 从中任取两个球;
(2)先取一球,取出后不放回,再取一球.
(3)先取一球,取出后放回,再取一球.
