高中数学人教新课标B版必修3--《3.1.1 随机事件的概率》 课件(共19张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修3--《3.1.1 随机事件的概率》 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 752.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 14:24:22 | ||
图片预览






文档简介
(共19张PPT)
奖项
中奖条件
红色球号码
蓝色球号码
一等奖
●●●●●●
●
二等奖
●●●●●●
三等奖
●●●●●
●
四
等
奖
●●●●●
●●●●
●
五等奖
●●●●
●●●
●
六等奖
●●
●
●
●
●
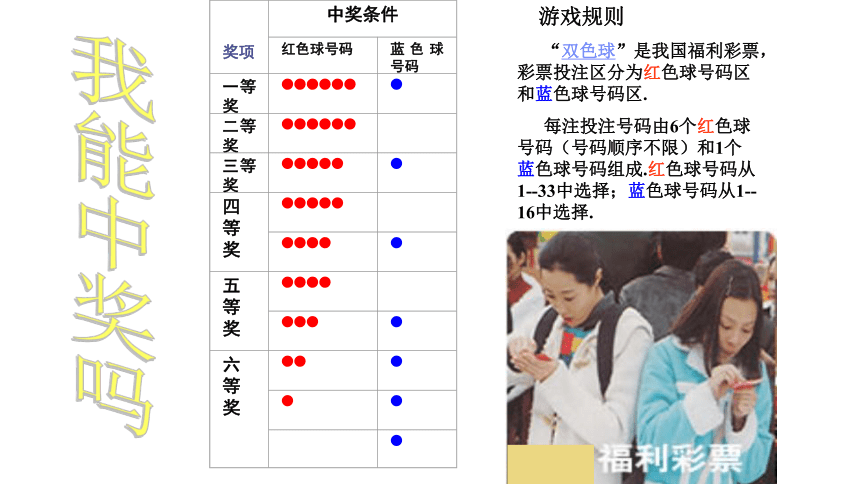
游戏规则
“双色球”是我国福利彩票, 彩票投注区分为红色球号码区和蓝色球号码区.
每注投注号码由6个红色球号码(号码顺序不限)和1个蓝色球号码组成.红色球号码从1--33中选择;蓝色球号码从1--16中选择.
学习目标
(1)结合实例了解必然事件,不可能事件,随机事件的概念;
(2)通过抛币试验了解随机事件的发生在大量重复试验下,呈现规律性,从而理解频率的稳定性及概率的统计定义;
(3)结合概率的统计定义理解频率与概率的区别和联系.
学习重点、难点
重点:理解频率的稳定性及概率的统计定义.
难点:频率与概率的区别和联系.
(1)“导体通电时,发热” ;
(2)“抛一石块,下落” ;
(3)“在标准大气压下且温度低于0oC时,冰融化 ”;
(4)“在常温下,焊锡融化” ;
(5)“某人射击一次,中靶” ;
(6)“掷一枚硬币,出现正面”.
---------------必然发生
---------------必然发生
-------不可能发生
-------不可能发生
---可能发生、也可能不发生
---可能发生、也可能不发生
下列事件是否发生,各有什么特点?
1、事件的分类
(1)“导体通电时,发热”;
(2)“抛一石块,下落”;
(3)“在标准大气压下且温度低于0oC时,冰融化”;
(4)“在常温下,焊锡融化”;
(5)“某人射击一次,中靶”;
(6)“掷一枚硬币,出现正面”...
---------------必然发生
---------------必然发生
-------不可能发生
-------不可能发生
---可能发生、也可能不发生
---可能发生、也可能不发生
必然事件
不可能事件
随机事件
在条件S下一定会发生的事件,叫做相对于条件S的必然事件,简称必然事件;
必然事件、不可能事件与随机事件
在条件S下一定不会发生的事件,叫做相对于条件S的不可能事件,简称不可能事件;
在条件S下可能发生也可能不发生的事件,叫做相对于条件S的随机事件,简称随机事件.
确定事件
必然事件、不可能事件与随机事件
指出下列事件是必然事件,不可能事件,还是随机事件:
例1
(1)“某电话机在一分钟之内,收到三次呼叫”;
(2)“当 x 是实数时,x2 ≥ 0”;
(3)“没有水分,种子发芽”;
(4)“打开电视机,正在播放新闻” .
你能举出一些现实生活中的随机事件、必然事件、不可能事件的实例吗?
如何才能获得随机事件发生的可能性大小呢?
最直接的方法就是试验(观察)
思考?
让我们来做抛掷硬币试验
(1)试验目的 探究随机事件“抛掷一枚硬币,正面朝上”发生的可能性大小;
(2)试验要求 每人做 10次 抛掷硬币试验,记录正面朝上的次数,并计算正面朝上的比例,然后各组长进行统计将试验结果填入下表中:
实验次数 正面朝上的次数 正面朝上的比例
10 0 0
10 1 0.1
10 2 0.2
10 3 0.3
10 4 0.4
10 ......
10 10 1
【规则(1)硬币统一(1角硬币);(2)垂直下抛;(3)离桌面高度大约为30cm.】
2.试验、观察和归纳
2、思考与讨论:
1.以上试验中,正面朝上的次数nA叫做 ,事件A出现的次数nA
与总实验次数n的比例叫做事件A出现的 . 即 .
2. 必然事件的频率为 ,不可能事件的频率为 ,频率的取值范围是 .
3.试验结果与其他同学比较,你的结果和他们一致吗?为什么
4.如果我们来做大量的重复抛掷硬币的试验,正面朝上的频率值会有什么规律吗?
频率本身是随机的,是一个变量。
频数
频率fn(A)
[0,1]
1
0
抛掷次数 2048 4040 12000 24000 30000 72088
正面朝上次数 1061 2048 6019 12012 14984 36124
频率 0.5181 0.5069 0.5016 0.5005 0 .4995 0.5011
历史上一些著名的抛币试验结果表
皮尔逊
皮尔逊
维 尼
蒲 丰
德 . 摩根
维 尼
结论:“掷一枚硬币,正面朝上”在一次试验中是否发生不能确定,但随着试验次数的增加,正面朝上的频率逐渐地接近于0.5.
随机事件A在一次试验中是否发生是不能预知的,但是在大量重复实验后,随着次数的增加,事件A发生的频率会逐渐稳定在某个常数上.
结论:
对于给定的随机事件A,如果随着试验次数的增加,事件A发生的频率fn(A)稳定在区间[0,1]中的某个常数上,把这个常数称为事件A的概率,记作P(A),简称为A的概率.
(1)概率的范围是 ,不可能事件的概率为 ,必然事件为 ,随机事件的概率 ;
(2)概率从数量上反映了一个事件发生的可能性的大小.
3、概率的定义
[0,1]
0
1
(0,1)
思考 频率是否等同于概率呢?
(1)随着试验次数的增加,频率会越来越接近概率;
(2)频率本身是随机的,在试验前不能确定;
(3)概率是一个确定的数,是客观存在的,与每次试验无关;
4、概率与频率的关系:
因此在实际中我们求一个事件的概率时,有时通过进行大量的重复试验,用这个事件发生的频率近似地作为它的概率.
判断对错
1.抛一枚硬币有可能出现正面也有可能出现反面。
2.抛一枚硬币出现正面向上的概率为0.5,所以抛两次时,肯定有一次是正面向上。
3.抛一枚硬币出现正面向上的概率为0.5,所以抛12000次时,出现正面向上的次数可能为6000 。
5、随堂练习:
(1)、下列事件:
①口袋里有伍角、壹角、壹元的硬币若干枚,随机地摸出一枚是壹角;
②在标准大气压下,水在90℃沸腾;
③射击运动员射击一次命中10环;
④同时掷两颗骰子,出现的点数之和不超过12.
其中是随机事件的有 ( )
A、① B、①② C、①③ D、②④
(2)、下列事件:
①如果a、b∈R,则a+b=b+a;
②“地球不停地转动”;
③明天西宁下雨;
④某人购买福利彩票中奖;
其中是必然事件的有 ( )
A、①② B、①②③ C、 ①④ D、②③
C
A
(3)、下列事件:
① a,b∈R且a②小华将一石块抛出地球;
③掷一枚硬币,正面向上;
④掷一颗骰子出现点8.
其中是不可能事件的是 ( )
A、①② B、②③ C、②④ D、①④
(4)、事件A发生的概率P(A)满足 ( )
(A) P(A)=0 (B) P(A)=1
(C) 0≤P(A)≤1 (D) 0C
C
(5)、某射手在同一条件下进行射击,结果如下:
射击次数n 10 20 50 100 200 500
击中靶心的次数 m 8 19 44 92 178 455
击中靶心的频率m/n
0.8
0.95
0.88
0.92
0.89
0.91
(1)计算表中击中靶心的各个频率;
(2)这个射手射击一次,击中靶心的概率约为多少?
0.9
(1)事件的分类:必然事件、不可能事件和随机事件;
(2)随机事件概率的定义;
(3)频率与概率的关系;
(4)统计的思想方法—试验、观察、探究、归纳和总结.
6.
奖项
中奖条件
红色球号码
蓝色球号码
一等奖
●●●●●●
●
二等奖
●●●●●●
三等奖
●●●●●
●
四
等
奖
●●●●●
●●●●
●
五等奖
●●●●
●●●
●
六等奖
●●
●
●
●
●
游戏规则
“双色球”是我国福利彩票, 彩票投注区分为红色球号码区和蓝色球号码区.
每注投注号码由6个红色球号码(号码顺序不限)和1个蓝色球号码组成.红色球号码从1--33中选择;蓝色球号码从1--16中选择.
学习目标
(1)结合实例了解必然事件,不可能事件,随机事件的概念;
(2)通过抛币试验了解随机事件的发生在大量重复试验下,呈现规律性,从而理解频率的稳定性及概率的统计定义;
(3)结合概率的统计定义理解频率与概率的区别和联系.
学习重点、难点
重点:理解频率的稳定性及概率的统计定义.
难点:频率与概率的区别和联系.
(1)“导体通电时,发热” ;
(2)“抛一石块,下落” ;
(3)“在标准大气压下且温度低于0oC时,冰融化 ”;
(4)“在常温下,焊锡融化” ;
(5)“某人射击一次,中靶” ;
(6)“掷一枚硬币,出现正面”.
---------------必然发生
---------------必然发生
-------不可能发生
-------不可能发生
---可能发生、也可能不发生
---可能发生、也可能不发生
下列事件是否发生,各有什么特点?
1、事件的分类
(1)“导体通电时,发热”;
(2)“抛一石块,下落”;
(3)“在标准大气压下且温度低于0oC时,冰融化”;
(4)“在常温下,焊锡融化”;
(5)“某人射击一次,中靶”;
(6)“掷一枚硬币,出现正面”...
---------------必然发生
---------------必然发生
-------不可能发生
-------不可能发生
---可能发生、也可能不发生
---可能发生、也可能不发生
必然事件
不可能事件
随机事件
在条件S下一定会发生的事件,叫做相对于条件S的必然事件,简称必然事件;
必然事件、不可能事件与随机事件
在条件S下一定不会发生的事件,叫做相对于条件S的不可能事件,简称不可能事件;
在条件S下可能发生也可能不发生的事件,叫做相对于条件S的随机事件,简称随机事件.
确定事件
必然事件、不可能事件与随机事件
指出下列事件是必然事件,不可能事件,还是随机事件:
例1
(1)“某电话机在一分钟之内,收到三次呼叫”;
(2)“当 x 是实数时,x2 ≥ 0”;
(3)“没有水分,种子发芽”;
(4)“打开电视机,正在播放新闻” .
你能举出一些现实生活中的随机事件、必然事件、不可能事件的实例吗?
如何才能获得随机事件发生的可能性大小呢?
最直接的方法就是试验(观察)
思考?
让我们来做抛掷硬币试验
(1)试验目的 探究随机事件“抛掷一枚硬币,正面朝上”发生的可能性大小;
(2)试验要求 每人做 10次 抛掷硬币试验,记录正面朝上的次数,并计算正面朝上的比例,然后各组长进行统计将试验结果填入下表中:
实验次数 正面朝上的次数 正面朝上的比例
10 0 0
10 1 0.1
10 2 0.2
10 3 0.3
10 4 0.4
10 ......
10 10 1
【规则(1)硬币统一(1角硬币);(2)垂直下抛;(3)离桌面高度大约为30cm.】
2.试验、观察和归纳
2、思考与讨论:
1.以上试验中,正面朝上的次数nA叫做 ,事件A出现的次数nA
与总实验次数n的比例叫做事件A出现的 . 即 .
2. 必然事件的频率为 ,不可能事件的频率为 ,频率的取值范围是 .
3.试验结果与其他同学比较,你的结果和他们一致吗?为什么
4.如果我们来做大量的重复抛掷硬币的试验,正面朝上的频率值会有什么规律吗?
频率本身是随机的,是一个变量。
频数
频率fn(A)
[0,1]
1
0
抛掷次数 2048 4040 12000 24000 30000 72088
正面朝上次数 1061 2048 6019 12012 14984 36124
频率 0.5181 0.5069 0.5016 0.5005 0 .4995 0.5011
历史上一些著名的抛币试验结果表
皮尔逊
皮尔逊
维 尼
蒲 丰
德 . 摩根
维 尼
结论:“掷一枚硬币,正面朝上”在一次试验中是否发生不能确定,但随着试验次数的增加,正面朝上的频率逐渐地接近于0.5.
随机事件A在一次试验中是否发生是不能预知的,但是在大量重复实验后,随着次数的增加,事件A发生的频率会逐渐稳定在某个常数上.
结论:
对于给定的随机事件A,如果随着试验次数的增加,事件A发生的频率fn(A)稳定在区间[0,1]中的某个常数上,把这个常数称为事件A的概率,记作P(A),简称为A的概率.
(1)概率的范围是 ,不可能事件的概率为 ,必然事件为 ,随机事件的概率 ;
(2)概率从数量上反映了一个事件发生的可能性的大小.
3、概率的定义
[0,1]
0
1
(0,1)
思考 频率是否等同于概率呢?
(1)随着试验次数的增加,频率会越来越接近概率;
(2)频率本身是随机的,在试验前不能确定;
(3)概率是一个确定的数,是客观存在的,与每次试验无关;
4、概率与频率的关系:
因此在实际中我们求一个事件的概率时,有时通过进行大量的重复试验,用这个事件发生的频率近似地作为它的概率.
判断对错
1.抛一枚硬币有可能出现正面也有可能出现反面。
2.抛一枚硬币出现正面向上的概率为0.5,所以抛两次时,肯定有一次是正面向上。
3.抛一枚硬币出现正面向上的概率为0.5,所以抛12000次时,出现正面向上的次数可能为6000 。
5、随堂练习:
(1)、下列事件:
①口袋里有伍角、壹角、壹元的硬币若干枚,随机地摸出一枚是壹角;
②在标准大气压下,水在90℃沸腾;
③射击运动员射击一次命中10环;
④同时掷两颗骰子,出现的点数之和不超过12.
其中是随机事件的有 ( )
A、① B、①② C、①③ D、②④
(2)、下列事件:
①如果a、b∈R,则a+b=b+a;
②“地球不停地转动”;
③明天西宁下雨;
④某人购买福利彩票中奖;
其中是必然事件的有 ( )
A、①② B、①②③ C、 ①④ D、②③
C
A
(3)、下列事件:
① a,b∈R且a
③掷一枚硬币,正面向上;
④掷一颗骰子出现点8.
其中是不可能事件的是 ( )
A、①② B、②③ C、②④ D、①④
(4)、事件A发生的概率P(A)满足 ( )
(A) P(A)=0 (B) P(A)=1
(C) 0≤P(A)≤1 (D) 0
C
(5)、某射手在同一条件下进行射击,结果如下:
射击次数n 10 20 50 100 200 500
击中靶心的次数 m 8 19 44 92 178 455
击中靶心的频率m/n
0.8
0.95
0.88
0.92
0.89
0.91
(1)计算表中击中靶心的各个频率;
(2)这个射手射击一次,击中靶心的概率约为多少?
0.9
(1)事件的分类:必然事件、不可能事件和随机事件;
(2)随机事件概率的定义;
(3)频率与概率的关系;
(4)统计的思想方法—试验、观察、探究、归纳和总结.
6.
