高中数学人教新课标B版必修3--《2.3.1 变量间的相关关系》教学设计(表格式)
文档属性
| 名称 | 高中数学人教新课标B版必修3--《2.3.1 变量间的相关关系》教学设计(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 166.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 14:33:55 | ||
图片预览


文档简介
课题:2.3.1变量间的相关关系
教材:普通高中课程标准实验教科书数学必修3 人教B版
课题 2.3.1 变量间的相关关系
教学目标 1.知识与技能(1)理解相关关系与函数关系的区别;(2)能根据两个有关联变量的数据作出散点图;(3)利用散点图直观认识两变量的相关关系.2.过程与方法(1)通过类比函数概念,体会统计思维与确定性思维的差异,注意到统计结果的随机性;(2)通过举例,体会相关关系在现实中是大量存在的,了解研究相关关系的必要性;(3)通过类比函数的研究方法,来研究相关关系,体会数学中类比的思想,学会用已学的知识来探索解决未知的知识.3.情感态度与价值观现代社会是信息化社会,人们常常需要收集数据,根据所获得的数据提取有价值的信息,作出合理决策.学习变量间的相关关系,可以解决此类问题,增强学生分析问题解决问题的能力.
教学重点 通过收集现实问题中两个有关联变量的数据作出散点图并判断两变量是否具有相关关系.
教学难点 利用散点图认识变量间的相关关系。
教学方法 教师引导学生进行小组合作,探索,讨论.
技术准备 PPT,EXCEL,实物展示台.
教学教程 师生互动 设计意图
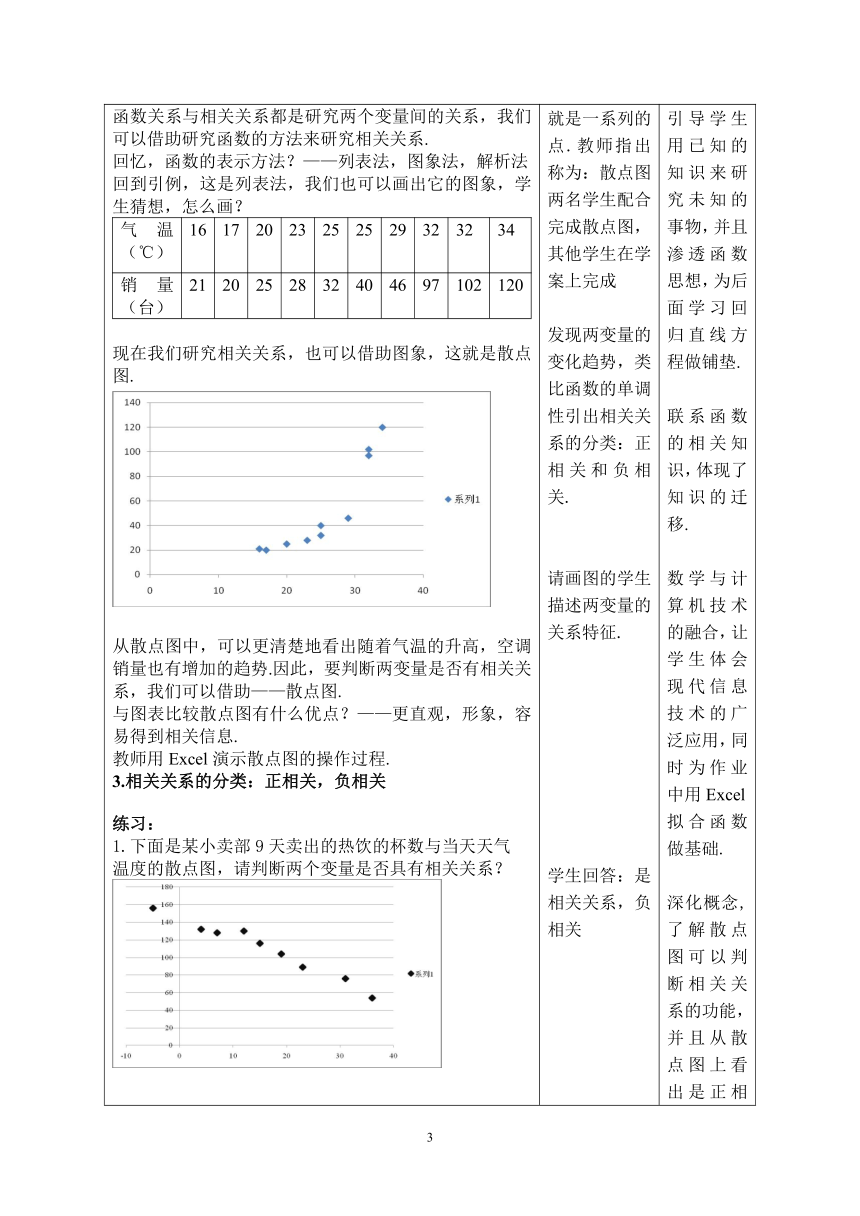
一、复习引入 世间万物都在发生变化,对于两个变化的量,如正方形的面积与边长的关系,可以称为(函数)关系 函数的概念:设集合A是一个非空数集,对A中的任意数x,按照确定的法则f,都有唯一确定的数y与它对应,则这种关系叫做集合A上的一个函数.强调三要素:定义域,值域,对应法则.对应法则必须是确定的,而且允许一对一,多对一,不允许一对多二、情景设置 看一段新闻视频,请你找出其中有几组变量,它们之间是否具有函数关系?气温升高——空调热卖气温升高——感冒的人增多气温升高——游泳的人增多从新闻中抽取一个实例,某商场在5月中的10天空调的销量(台)与气温(℃)的关系,如下表:气温(℃)16172023252529323234销量(台)21 20 25 25 32 40 46 97 102 120 预期结果:学生说出与函数关系的不同之处:可以“一对多”;没有一个确定的关系式;当确定温度值时,无法计算销量等.强调不确定性,影响销量的因素有很多,不一定只有温度.生活当中大量的存在这样看起来有关系,但又不确定,我们称这种关系为相关关系.请学生通过自己的理解说出相关关系有什么特点?三、概念形成1.相关关系概念:两变量间确实存在关系,但又不具备函数关系所要求的确定性,它们的关系带有随机性的,就称为变量间的相关关系.四、概念深化判断下列两变量的关系是相关关系还是函数关系1.正方体的棱长与体积的关系;2.人的年龄与他拥有财富之间的关系;3.电压一定时,电流与电阻的关系;4.某产品在广告上的投资与销售量之间的关系你能举出相关关系的例子吗? 2.散点图如何判断两变量之间是否有相关关系?我们可以借助日常生活经验对一些常规问题来进行定性分析,但是定性分析有时会给我们以误导,也无法确定变量之间相互影响的程度有多大.数学是说理的,需要用数字来说话,因此,我们还需要进行定量分析.函数关系与相关关系都是研究两个变量间的关系,我们可以借助研究函数的方法来研究相关关系.回忆,函数的表示方法?——列表法,图象法,解析法回到引例,这是列表法,我们也可以画出它的图象,学生猜想,怎么画?气温(℃)1617202325252932 32 34 销量(台)21 20 25 28 32 40 46 97 102 120 现在我们研究相关关系,也可以借助图象,这就是散点图.从散点图中,可以更清楚地看出随着气温的升高,空调销量也有增加的趋势.因此,要判断两变量是否有相关关系,我们可以借助——散点图.与图表比较散点图有什么优点?——更直观,形象,容易得到相关信息.教师用Excel演示散点图的操作过程.3.相关关系的分类:正相关,负相关练习:1.下面是某小卖部9天卖出的热饮的杯数与当天天气 温度的散点图,请判断两个变量是否具有相关关系?2. 请判断以下两个变量是否具有相关关系? 有的同学可能有这样的疑问:我们为什么要学习相关关系呢?函数关系是一种理想的关系模型,而相关关系是更为一般的情况,因此研究相关关系可以处理更广泛的数学问题.五、学生活动(一)给出本班10名学生期中考试的数学以及物理成绩,请对成绩进行分析:姓名数学物理夏晗7780张铭梁7473何颖媛6973支张6961薛闻达6763拉巴雍措6654李泽昂6056孙雨5948杜思旭5537具浩宇48281.画出散点图,并判断是否具有相关关系? 2.通过分析,你能得到什么结论? 说明:“数理不分家”,它们之间的关系是正相关.事实上,两个成绩都是随机变量.1.影响成绩的因素有哪些?2.假如一名同学的数学成绩是70分,你能估测他的物理成绩吗?从趋势上看,可以估计是60分左右,但是不能确定,因为影响物理成绩的因素有很多.从整体上看,散点图的形状接近什么函数?——一次函数,所以我们可以用一次函数来对散点图进行拟合.定性分析——定量分析——进行预测 (二)回到引例,气温升高空调销量上升,假如你是销售部经理,明天的气温是31℃,你该作何准备?看视频截取,卖场经理也在做预测如何画出这条直线?在画直线时,怎样能更贴近它的真实值是下节课的内容.六、课堂小结:1.这节课你的收获? 辨析相关关系与函数关系的异同点函数关系相关关系相同点两个变量间的关系不同点关系确定关系不确定,有随机性2.思想方法 类比 3.对于这节课的内容你还有什么困惑?七、布置作业:1.教材P74 A2已知学生身高与体重的关系,做出散点图,并分析数据的特点;2.预习思考: (1)在Excel上操作实验,可以用什么函数对例题中的相关关系进行拟合? (2)如何求最优拟合直线的方程? 复习函数概念学生回答教师引导学生关注函数关系的特点.学生看新闻视频,小组讨论2分钟. 从中找到变量,辨析出每组变量之间的关系不是函数关系.观察数据特征,小组讨论,说出以上两个变量是不是函数关系?为什么?教师板书课题,学生试着说出相关关系的特点学生回答学生举例教师讲解学生回答函数的表示方法,并猜测相关关系的图象表示就是一系列的点.教师指出称为:散点图两名学生配合完成散点图,其他学生在学案上完成发现两变量的变化趋势,类比函数的单调性引出相关关系的分类:正相关和负相关.请画图的学生描述两变量的关系特征.学生回答:是相关关系,负相关学生回答:没有规律,是离散的点,不具有相关关系,学生活动5分钟,先独自完成散点图,再分析数据特征.教师巡视,进行指导.展示台展示学生作图,并提问学生回答问题1,是相关关系,是正相关.提问成绩较好的同学,说出影响成绩的因素.提问学生,关注学生的回答,进行分析解释.截取视频中预测一段,引导学生从整体趋势上预测,并估测可以用什么函数进行拟合.学生总结,教师给出表格,让学生在此对相关关系和函数关系进行辨析.经历了定性分析——定量分析——进行预测的思维过程学生课下完成,既总结本节课又为下节课做准备. 通过复习函数概念,让学生意识到函数关系重要的是确定性,为后面辨析相关关系做铺垫.以生活实际问题为背景,提出问题.此时学生可能还会认为片中的关系是函数关系,因此抽取视频中的一个问题,让学生从数字上去体会两变量关系并不是函数关系.学生经历归纳——总结——猜想的过程,有助于数学思维的发展.关注学生的最近发展区类比函数的研究方法来研究相关关系,引导学生用已知的知识来研究未知的事物,并且渗透函数思想,为后面学习回归直线方程做铺垫.联系函数的相关知识,体现了知识的迁移.数学与计算机技术的融合,让学生体会现代信息技术的广泛应用,同时为作业中用Excel拟合函数做基础.深化概念,了解散点图可以判断相关关系的功能,并且从散点图上看出是正相关还是负相关,深刻体会到散点图的作用.让学生体会到数学的重要性,它是学好其他理科的必备工具.并对学习方法进行总结,引导学生如何学好数学. 让学生体会到研究相关关系对学习生活是有帮助的.利用函数图象可以拟合两变量的相关关系,并进行预测.前后呼应,让学生相关关系可以用不同的函数去拟合,而线性相关是我们即将研究的一项内容,引起学生的兴趣,激发求知欲,为下节课的内容埋下伏笔本节课的内容有全面的理解深化概念以表格的形式给出,突出重点,对比两种关系的不同点
八、板书 2.3.1变量间的相关关系一、相关关系 二、散点图1.有关系 2.不确定 (图)3.随机的性三、分类:正相关、负相关投影函数:确定性定性——定量——预测 数学成绩 物理成绩影响因素
九、教学反思
在前面的学习中,学生对统计学有了一定的认识和理解,在生活中统计学应用很广泛。学生原来接触的两变量之间的关系是函数关系,但是在生活中,两变量间的关系不都是确定的,这就需要引进相关关系。学生对此还是有一定认识,并且能够体会到这种关系。因此,将学习分为如下几部分:
一、认识相关关系:通过观看新闻视频,引入相关关系.但是开始学生还不能分辨相关关系,这时给出新闻中的一组变量的数据,从数字上分析两变量的关系不是函数关系.
二、理解相关关系:
1、给出几个例子,让学生判断是函数关系还是相关关系,再次将其与函数关系进行比较,深化概念.
三、定量分析:将判断相关关系上升到理性思维,画散点图,根据图象来判断两变量之间的关系,趋势等。
四、操作阶段:学生动手画散点图,并对数据进行分析,判断是不是相关关系。并根据散点图预测结果。以此,激发学生的学习兴趣,并为下节课的学习做好铺垫。
五、预测阶段:
本节课的不足之处:
1.在引例中,应更详细的解释什么是随机变量,如空调的销量不止与气温有关,还与人们的需求量,收入,交通状况等都会使得销量发生变化.
2.应更加关注学生的思维.如学生在举例说明相关关系时,应再引导,多举些例子,并且这些实例能够给体现出数字的关系,便于定量研究。
十、课堂教学流程图
开始
教学引入
判断气温与空调销量的关系是不是函数关系
找出三组变量
学生小组讨论
教师巡视、指导
新闻视频
辨析函数关系与相关关系,并举例
类比函数得出散点图
学生板演画散点图
教师巡视、指导
学生反馈讨论结果,形成概念
学生分析数据,教师Excel作图
学生根据散点图判断相关关系
数学成绩与物理成绩的关系
课堂小结
布置作业
结束
学生分析数据,分享学习方法
学生画散点图
教师巡视、指导
回到引例,进行预测
学生讲解
PAGE
7
教材:普通高中课程标准实验教科书数学必修3 人教B版
课题 2.3.1 变量间的相关关系
教学目标 1.知识与技能(1)理解相关关系与函数关系的区别;(2)能根据两个有关联变量的数据作出散点图;(3)利用散点图直观认识两变量的相关关系.2.过程与方法(1)通过类比函数概念,体会统计思维与确定性思维的差异,注意到统计结果的随机性;(2)通过举例,体会相关关系在现实中是大量存在的,了解研究相关关系的必要性;(3)通过类比函数的研究方法,来研究相关关系,体会数学中类比的思想,学会用已学的知识来探索解决未知的知识.3.情感态度与价值观现代社会是信息化社会,人们常常需要收集数据,根据所获得的数据提取有价值的信息,作出合理决策.学习变量间的相关关系,可以解决此类问题,增强学生分析问题解决问题的能力.
教学重点 通过收集现实问题中两个有关联变量的数据作出散点图并判断两变量是否具有相关关系.
教学难点 利用散点图认识变量间的相关关系。
教学方法 教师引导学生进行小组合作,探索,讨论.
技术准备 PPT,EXCEL,实物展示台.
教学教程 师生互动 设计意图
一、复习引入 世间万物都在发生变化,对于两个变化的量,如正方形的面积与边长的关系,可以称为(函数)关系 函数的概念:设集合A是一个非空数集,对A中的任意数x,按照确定的法则f,都有唯一确定的数y与它对应,则这种关系叫做集合A上的一个函数.强调三要素:定义域,值域,对应法则.对应法则必须是确定的,而且允许一对一,多对一,不允许一对多二、情景设置 看一段新闻视频,请你找出其中有几组变量,它们之间是否具有函数关系?气温升高——空调热卖气温升高——感冒的人增多气温升高——游泳的人增多从新闻中抽取一个实例,某商场在5月中的10天空调的销量(台)与气温(℃)的关系,如下表:气温(℃)16172023252529323234销量(台)21 20 25 25 32 40 46 97 102 120 预期结果:学生说出与函数关系的不同之处:可以“一对多”;没有一个确定的关系式;当确定温度值时,无法计算销量等.强调不确定性,影响销量的因素有很多,不一定只有温度.生活当中大量的存在这样看起来有关系,但又不确定,我们称这种关系为相关关系.请学生通过自己的理解说出相关关系有什么特点?三、概念形成1.相关关系概念:两变量间确实存在关系,但又不具备函数关系所要求的确定性,它们的关系带有随机性的,就称为变量间的相关关系.四、概念深化判断下列两变量的关系是相关关系还是函数关系1.正方体的棱长与体积的关系;2.人的年龄与他拥有财富之间的关系;3.电压一定时,电流与电阻的关系;4.某产品在广告上的投资与销售量之间的关系你能举出相关关系的例子吗? 2.散点图如何判断两变量之间是否有相关关系?我们可以借助日常生活经验对一些常规问题来进行定性分析,但是定性分析有时会给我们以误导,也无法确定变量之间相互影响的程度有多大.数学是说理的,需要用数字来说话,因此,我们还需要进行定量分析.函数关系与相关关系都是研究两个变量间的关系,我们可以借助研究函数的方法来研究相关关系.回忆,函数的表示方法?——列表法,图象法,解析法回到引例,这是列表法,我们也可以画出它的图象,学生猜想,怎么画?气温(℃)1617202325252932 32 34 销量(台)21 20 25 28 32 40 46 97 102 120 现在我们研究相关关系,也可以借助图象,这就是散点图.从散点图中,可以更清楚地看出随着气温的升高,空调销量也有增加的趋势.因此,要判断两变量是否有相关关系,我们可以借助——散点图.与图表比较散点图有什么优点?——更直观,形象,容易得到相关信息.教师用Excel演示散点图的操作过程.3.相关关系的分类:正相关,负相关练习:1.下面是某小卖部9天卖出的热饮的杯数与当天天气 温度的散点图,请判断两个变量是否具有相关关系?2. 请判断以下两个变量是否具有相关关系? 有的同学可能有这样的疑问:我们为什么要学习相关关系呢?函数关系是一种理想的关系模型,而相关关系是更为一般的情况,因此研究相关关系可以处理更广泛的数学问题.五、学生活动(一)给出本班10名学生期中考试的数学以及物理成绩,请对成绩进行分析:姓名数学物理夏晗7780张铭梁7473何颖媛6973支张6961薛闻达6763拉巴雍措6654李泽昂6056孙雨5948杜思旭5537具浩宇48281.画出散点图,并判断是否具有相关关系? 2.通过分析,你能得到什么结论? 说明:“数理不分家”,它们之间的关系是正相关.事实上,两个成绩都是随机变量.1.影响成绩的因素有哪些?2.假如一名同学的数学成绩是70分,你能估测他的物理成绩吗?从趋势上看,可以估计是60分左右,但是不能确定,因为影响物理成绩的因素有很多.从整体上看,散点图的形状接近什么函数?——一次函数,所以我们可以用一次函数来对散点图进行拟合.定性分析——定量分析——进行预测 (二)回到引例,气温升高空调销量上升,假如你是销售部经理,明天的气温是31℃,你该作何准备?看视频截取,卖场经理也在做预测如何画出这条直线?在画直线时,怎样能更贴近它的真实值是下节课的内容.六、课堂小结:1.这节课你的收获? 辨析相关关系与函数关系的异同点函数关系相关关系相同点两个变量间的关系不同点关系确定关系不确定,有随机性2.思想方法 类比 3.对于这节课的内容你还有什么困惑?七、布置作业:1.教材P74 A2已知学生身高与体重的关系,做出散点图,并分析数据的特点;2.预习思考: (1)在Excel上操作实验,可以用什么函数对例题中的相关关系进行拟合? (2)如何求最优拟合直线的方程? 复习函数概念学生回答教师引导学生关注函数关系的特点.学生看新闻视频,小组讨论2分钟. 从中找到变量,辨析出每组变量之间的关系不是函数关系.观察数据特征,小组讨论,说出以上两个变量是不是函数关系?为什么?教师板书课题,学生试着说出相关关系的特点学生回答学生举例教师讲解学生回答函数的表示方法,并猜测相关关系的图象表示就是一系列的点.教师指出称为:散点图两名学生配合完成散点图,其他学生在学案上完成发现两变量的变化趋势,类比函数的单调性引出相关关系的分类:正相关和负相关.请画图的学生描述两变量的关系特征.学生回答:是相关关系,负相关学生回答:没有规律,是离散的点,不具有相关关系,学生活动5分钟,先独自完成散点图,再分析数据特征.教师巡视,进行指导.展示台展示学生作图,并提问学生回答问题1,是相关关系,是正相关.提问成绩较好的同学,说出影响成绩的因素.提问学生,关注学生的回答,进行分析解释.截取视频中预测一段,引导学生从整体趋势上预测,并估测可以用什么函数进行拟合.学生总结,教师给出表格,让学生在此对相关关系和函数关系进行辨析.经历了定性分析——定量分析——进行预测的思维过程学生课下完成,既总结本节课又为下节课做准备. 通过复习函数概念,让学生意识到函数关系重要的是确定性,为后面辨析相关关系做铺垫.以生活实际问题为背景,提出问题.此时学生可能还会认为片中的关系是函数关系,因此抽取视频中的一个问题,让学生从数字上去体会两变量关系并不是函数关系.学生经历归纳——总结——猜想的过程,有助于数学思维的发展.关注学生的最近发展区类比函数的研究方法来研究相关关系,引导学生用已知的知识来研究未知的事物,并且渗透函数思想,为后面学习回归直线方程做铺垫.联系函数的相关知识,体现了知识的迁移.数学与计算机技术的融合,让学生体会现代信息技术的广泛应用,同时为作业中用Excel拟合函数做基础.深化概念,了解散点图可以判断相关关系的功能,并且从散点图上看出是正相关还是负相关,深刻体会到散点图的作用.让学生体会到数学的重要性,它是学好其他理科的必备工具.并对学习方法进行总结,引导学生如何学好数学. 让学生体会到研究相关关系对学习生活是有帮助的.利用函数图象可以拟合两变量的相关关系,并进行预测.前后呼应,让学生相关关系可以用不同的函数去拟合,而线性相关是我们即将研究的一项内容,引起学生的兴趣,激发求知欲,为下节课的内容埋下伏笔本节课的内容有全面的理解深化概念以表格的形式给出,突出重点,对比两种关系的不同点
八、板书 2.3.1变量间的相关关系一、相关关系 二、散点图1.有关系 2.不确定 (图)3.随机的性三、分类:正相关、负相关投影函数:确定性定性——定量——预测 数学成绩 物理成绩影响因素
九、教学反思
在前面的学习中,学生对统计学有了一定的认识和理解,在生活中统计学应用很广泛。学生原来接触的两变量之间的关系是函数关系,但是在生活中,两变量间的关系不都是确定的,这就需要引进相关关系。学生对此还是有一定认识,并且能够体会到这种关系。因此,将学习分为如下几部分:
一、认识相关关系:通过观看新闻视频,引入相关关系.但是开始学生还不能分辨相关关系,这时给出新闻中的一组变量的数据,从数字上分析两变量的关系不是函数关系.
二、理解相关关系:
1、给出几个例子,让学生判断是函数关系还是相关关系,再次将其与函数关系进行比较,深化概念.
三、定量分析:将判断相关关系上升到理性思维,画散点图,根据图象来判断两变量之间的关系,趋势等。
四、操作阶段:学生动手画散点图,并对数据进行分析,判断是不是相关关系。并根据散点图预测结果。以此,激发学生的学习兴趣,并为下节课的学习做好铺垫。
五、预测阶段:
本节课的不足之处:
1.在引例中,应更详细的解释什么是随机变量,如空调的销量不止与气温有关,还与人们的需求量,收入,交通状况等都会使得销量发生变化.
2.应更加关注学生的思维.如学生在举例说明相关关系时,应再引导,多举些例子,并且这些实例能够给体现出数字的关系,便于定量研究。
十、课堂教学流程图
开始
教学引入
判断气温与空调销量的关系是不是函数关系
找出三组变量
学生小组讨论
教师巡视、指导
新闻视频
辨析函数关系与相关关系,并举例
类比函数得出散点图
学生板演画散点图
教师巡视、指导
学生反馈讨论结果,形成概念
学生分析数据,教师Excel作图
学生根据散点图判断相关关系
数学成绩与物理成绩的关系
课堂小结
布置作业
结束
学生分析数据,分享学习方法
学生画散点图
教师巡视、指导
回到引例,进行预测
学生讲解
PAGE
7
