第三章圆锥曲线的方程:圆圆相切求轨迹方程 学案-2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册(Word含答案)
文档属性
| 名称 | 第三章圆锥曲线的方程:圆圆相切求轨迹方程 学案-2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册(Word含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 166.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 00:00:00 | ||
图片预览


文档简介
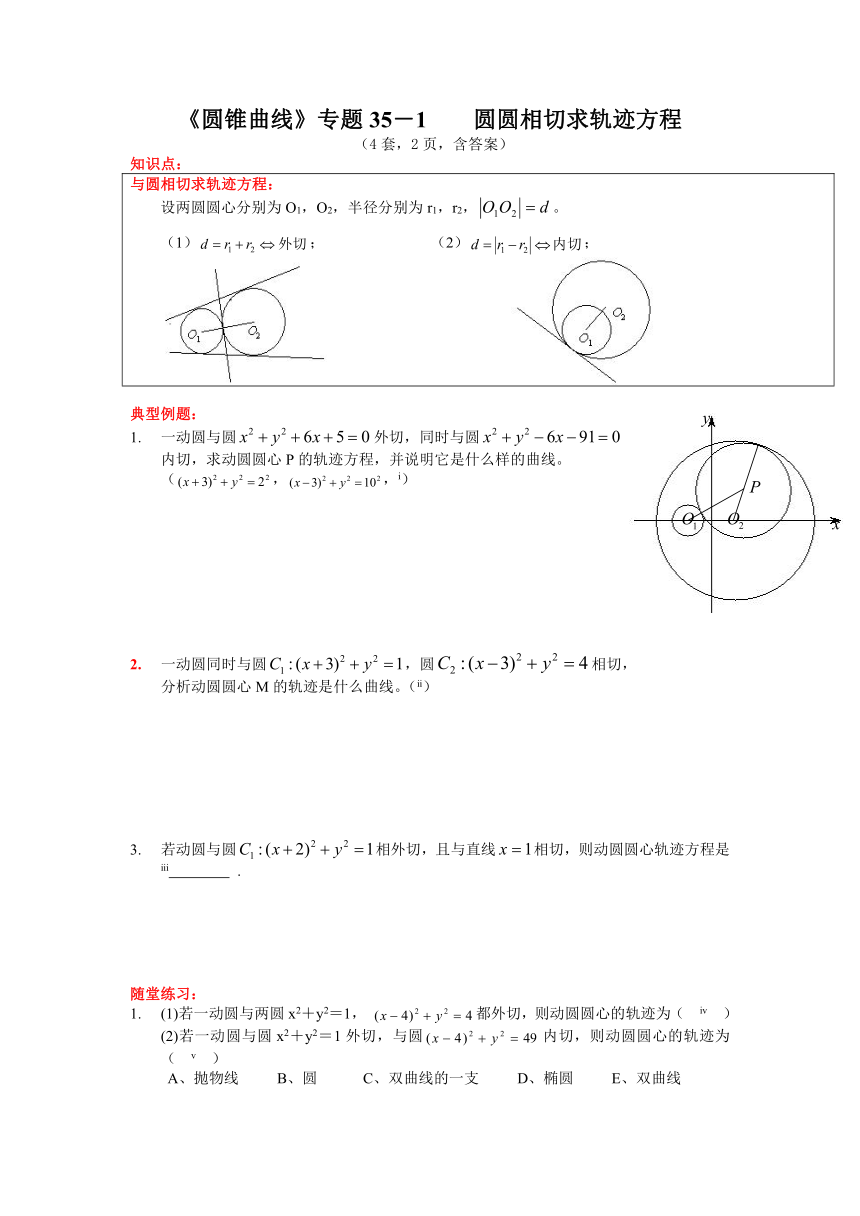
《圆锥曲线》专题35-1 圆圆相切求轨迹方程
(4套,2页,含答案)
知识点:
与圆相切求轨迹方程: 设两圆圆心分别为O1,O2,半径分别为r1,r2,。 (1); (2);
典型例题:
一动圆与圆外切,同时与圆
内切,求动圆圆心P的轨迹方程,并说明它是什么样的曲线。
(,,[endnoteRef:0])
[0: 答案:;
【解析】设动圆圆心为,半径为,设已知圆的圆心分别为、,
将圆方程分别配方得:,,
当与相切时,有 ①
当与相切时,有 ②
将①②两式的两边分别相加,得,
即 ③
移项再两边分别平方得:
④
两边再平方得:,
整理得,
所以,动圆圆心的轨迹方程是,轨迹是椭圆。]
一动圆同时与圆,圆相切,
分析动圆圆心M的轨迹是什么曲线。([endnoteRef:1])
[1: 答案:两组双曲线,即四条曲线;]
若动圆与圆相外切,且与直线相切,则动圆圆心轨迹方程是[endnoteRef:2] .
[2: 答案:;]
随堂练习:
(1)若一动圆与两圆x2+y2=1, 都外切,则动圆圆心的轨迹为( [endnoteRef:3] )
(2)若一动圆与圆x2+y2=1外切,与圆内切,则动圆圆心的轨迹为( [endnoteRef:4] )
A、抛物线 B、圆 C、双曲线的一支 D、椭圆 E、双曲线 [3: 答案:C;] [4: 答案:D;]
动圆M过定点P(-4,0),且与圆C:x2 + y2-8x = 0相切,求动圆圆心M的轨迹方程。
(配方:,答案:[endnoteRef:5]) [5: 答案:;]
与圆C:外切,又与y轴相切的圆的圆心的轨迹方程是( [endnoteRef:6] )
(A) (B)或 (C)或 (D)
(配方: ) [6: 答案:B;]
《圆锥曲线》专题35-2 圆圆相切求轨迹方程
设圆C与两圆中的一个内切,另一个外切.
求C的圆心轨迹L的方程;([endnoteRef:7]) [7: 答案:;]
已知动圆P与定圆C:(x+2)2+y2=1相外切,又与定直线l:x=1相切,那么动圆的圆心P的轨迹方程是_______.
《圆锥曲线》专题35-3 圆圆相切求轨迹方程
矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为,
点在AD边所在直线上.
(1)求AD边所在直线的方程;
(2)ABCD外接圆的方程;
(3)若动圆P过点,且与矩形ABCD的外接圆外切,求动圆P的圆心的轨迹方程.([endnoteRef:8])
[8: 答案:Y=-3x-2; ; ]
一动圆与圆外切,与圆内切.
(1)求动圆圆心M的轨迹L的方程;([endnoteRef:9]). [9: 答案:;
【解析】1)设动圆圆心为,半径为.
由题意,得,, . …………3分
由椭圆定义知在以为焦点的椭圆上,且,
.
动圆圆心M的轨迹的方程为. ……6分
(2) 如图,设内切圆N的半径为,与直线的切点为C,
则三角形的面积
=
当最大时,也最大, 内切圆的面积也最大, …………7分
设、(),则, ……8分
由,得,
解得,, …………10分
∴,令,则,且,
有,令,则,
当时,,在上单调递增,有,,
即当,时,有最大值,得,这时所求内切圆的面积为,
∴存在直线,的内切圆M的面积最大值为. …………14分
]
《圆锥曲线》专题35-4 圆圆相切求轨迹方程
动圆与两圆和都外切,则动圆圆心的轨迹为( [endnoteRef:10] )
A.抛物线 B.圆 C.双曲线的一支 D.椭圆
[10: 答案:C;]
(4套,2页,含答案)
知识点:
与圆相切求轨迹方程: 设两圆圆心分别为O1,O2,半径分别为r1,r2,。 (1); (2);
典型例题:
一动圆与圆外切,同时与圆
内切,求动圆圆心P的轨迹方程,并说明它是什么样的曲线。
(,,[endnoteRef:0])
[0: 答案:;
【解析】设动圆圆心为,半径为,设已知圆的圆心分别为、,
将圆方程分别配方得:,,
当与相切时,有 ①
当与相切时,有 ②
将①②两式的两边分别相加,得,
即 ③
移项再两边分别平方得:
④
两边再平方得:,
整理得,
所以,动圆圆心的轨迹方程是,轨迹是椭圆。]
一动圆同时与圆,圆相切,
分析动圆圆心M的轨迹是什么曲线。([endnoteRef:1])
[1: 答案:两组双曲线,即四条曲线;]
若动圆与圆相外切,且与直线相切,则动圆圆心轨迹方程是[endnoteRef:2] .
[2: 答案:;]
随堂练习:
(1)若一动圆与两圆x2+y2=1, 都外切,则动圆圆心的轨迹为( [endnoteRef:3] )
(2)若一动圆与圆x2+y2=1外切,与圆内切,则动圆圆心的轨迹为( [endnoteRef:4] )
A、抛物线 B、圆 C、双曲线的一支 D、椭圆 E、双曲线 [3: 答案:C;] [4: 答案:D;]
动圆M过定点P(-4,0),且与圆C:x2 + y2-8x = 0相切,求动圆圆心M的轨迹方程。
(配方:,答案:[endnoteRef:5]) [5: 答案:;]
与圆C:外切,又与y轴相切的圆的圆心的轨迹方程是( [endnoteRef:6] )
(A) (B)或 (C)或 (D)
(配方: ) [6: 答案:B;]
《圆锥曲线》专题35-2 圆圆相切求轨迹方程
设圆C与两圆中的一个内切,另一个外切.
求C的圆心轨迹L的方程;([endnoteRef:7]) [7: 答案:;]
已知动圆P与定圆C:(x+2)2+y2=1相外切,又与定直线l:x=1相切,那么动圆的圆心P的轨迹方程是_______.
《圆锥曲线》专题35-3 圆圆相切求轨迹方程
矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为,
点在AD边所在直线上.
(1)求AD边所在直线的方程;
(2)ABCD外接圆的方程;
(3)若动圆P过点,且与矩形ABCD的外接圆外切,求动圆P的圆心的轨迹方程.([endnoteRef:8])
[8: 答案:Y=-3x-2; ; ]
一动圆与圆外切,与圆内切.
(1)求动圆圆心M的轨迹L的方程;([endnoteRef:9]). [9: 答案:;
【解析】1)设动圆圆心为,半径为.
由题意,得,, . …………3分
由椭圆定义知在以为焦点的椭圆上,且,
.
动圆圆心M的轨迹的方程为. ……6分
(2) 如图,设内切圆N的半径为,与直线的切点为C,
则三角形的面积
=
当最大时,也最大, 内切圆的面积也最大, …………7分
设、(),则, ……8分
由,得,
解得,, …………10分
∴,令,则,且,
有,令,则,
当时,,在上单调递增,有,,
即当,时,有最大值,得,这时所求内切圆的面积为,
∴存在直线,的内切圆M的面积最大值为. …………14分
]
《圆锥曲线》专题35-4 圆圆相切求轨迹方程
动圆与两圆和都外切,则动圆圆心的轨迹为( [endnoteRef:10] )
A.抛物线 B.圆 C.双曲线的一支 D.椭圆
[10: 答案:C;]
