高中数学人教新课标B版必修3--《2.2.1 用样本的频率分布估计总体的分布》课件2(共28张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修3--《2.2.1 用样本的频率分布估计总体的分布》课件2(共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 00:00:00 | ||
图片预览





文档简介
(共28张PPT)
2.2.1用样本的
频率分布估计总体分布
第一课时
我国是世界上严重缺水的国家之一,
城市缺水问题较为突出。
2000年全国主要城市中缺水情况排在前10位的城市
引入
政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a , 用水量不超过a的部分按平价收费,超过a的部分按议价收费。
①如果希望大部分居民的日常生活不受影响,那 么标准a定为多少比较合理呢?
②为了较合理地确定这个标准,你认为需要做
哪些工作?
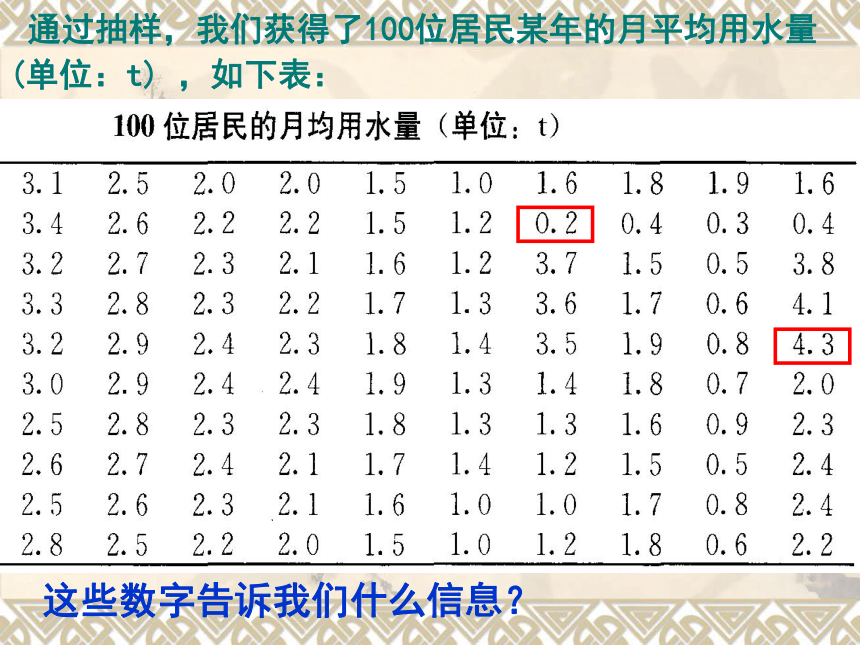
这些数字告诉我们什么信息?
通过抽样,我们获得了100位居民某年的月平均用水量(单位:t) ,如下表:
3.1 2.5 2.0 2.0 1.5 1.0 1.6 1.8 1.9 1.6
3.4 2.6 2.2 2.2 1.5 1.2 0.2 0.4 0.3 0.4
3.2 2.7 2.3 2.1 1.6. 1.2 3.7 1.5 0.5 3.8
3.3 2.8 2.3 2.2 1.7 1.2 3.6 1.7 0.6 4.1
3.2 2.9 2.4 2.3 1.8 1.3 3.5 1.9 0.8 4.3
3.0 2.9 2.4 2.4 1.9 1.4 1.4 1.8 0.7 2.0
2.5 2.8 2.3 2.3 1.8 1.3 1.3 1.6 0.9 2.3
2.6 2.7 2.4 2.1 1.7 1.3 1.2 1.5 0.5 2.4
2.5 2.6 2.3 2.1 1.6 1.4 1.0 1.7 0.8 2.4
2.8 2.5 2.2 2.0 1.5 1.0 1.2 1.8 0.6 2.2
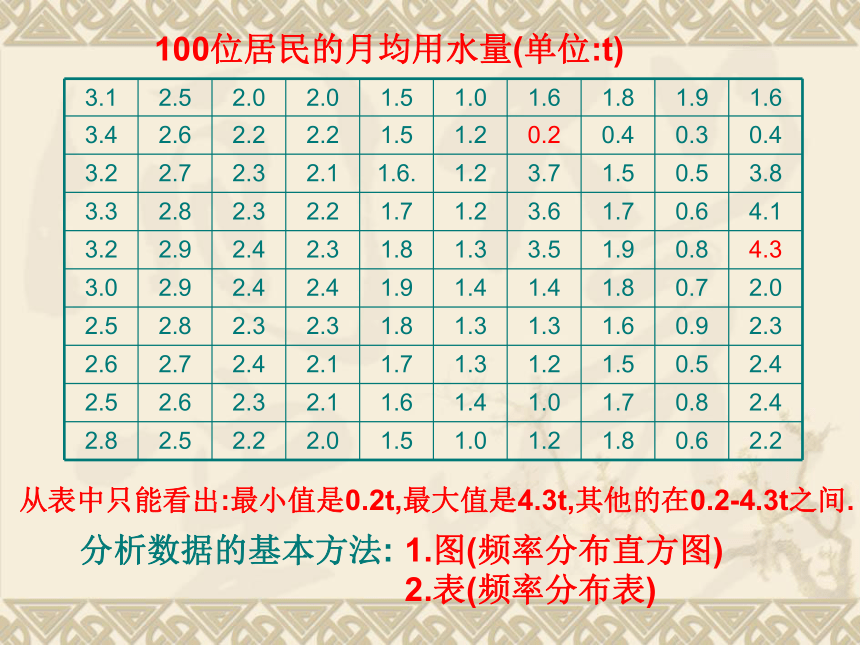
100位居民的月均用水量(单位:t)
从表中只能看出:最小值是0.2t,最大值是4.3t,其他的在0.2-4.3t之间.
分析数据的基本方法:
1.图(频率分布直方图)
2.表(频率分布表)
1.求极差(即一组数据中最大值与最小值的差)
2.决定组距与组数
4.3 - 0.2 = 4.1
4.1
0.5
= 8.2
组数=
组距
极差
=
3.将数据分组(左闭右开)
[0,0.5 ),[0.5,1 ),…,[4,4.5]
组数:将数据分组,当数据在100个以内时,
按数据多少常分5-12组。
组距:指每个小组的两个端点的距离,
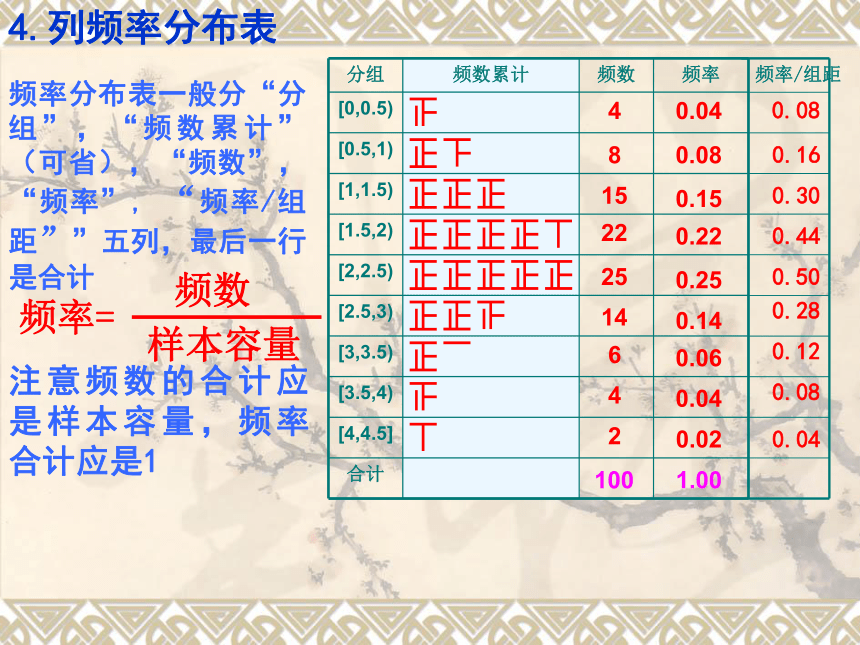
4.列频率分布表
分组 频数累计 频数 频率
[0,0.5)
[0.5,1)
[1,1.5)
[1.5,2)
[2,2.5)
[2.5,3)
[3,3.5)
[3.5,4)
[4,4.5]
合计
4
8
15
22
25
14
6
4
2
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
100
1.00
频率=
样本容量
频数
频率分布表一般分“分组”,“频数累计”(可省),“频数”,“频率”, “频率/组距””五列,最后一行是合计
注意频数的合计应是样本容量,频率合计应是1
0.02
频率/组距
0.08
0.16
0.30
0.44
0.50
0.28
0.12
0.08
0.04
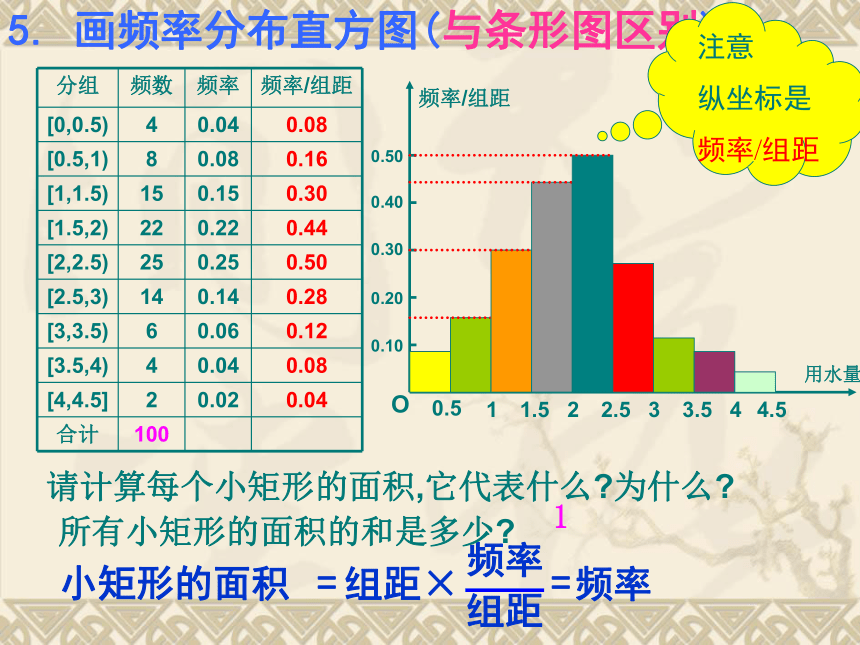
小矩形的面积
组距
频率
组距×
频率
=
=
分组 频数 频率 频率/组距
[0,0.5) 4 0.04 0.08
[0.5,1) 8 0.08 0.16
[1,1.5) 15 0.15 0.30
[1.5,2) 22 0.22 0.44
[2,2.5) 25 0.25 0.50
[2.5,3) 14 0.14 0.28
[3,3.5) 6 0.06 0.12
[3.5,4) 4 0.04 0.08
[4,4.5] 2 0.02 0.04
合计 100
5. 画频率分布直方图(与条形图区别):
用水量/t
0.10
0.20
0.30
0.40
0.50
O
频率/组距
0.5
1
1.5
2.5
3.5
4.5
2
3
4
请计算每个小矩形的面积,它代表什么 为什么
所有小矩形的面积的和是多少
1
注意
纵坐标是
频率/组距
用水量/t
0.10
0.20
0.30
0.40
0.50
O
频率/组距
0.5
1
1.5
2.5
3.5
4.5
2
3
4
频率分布直方图,显示了样本数据落在各个小组的比例的大小,图中最高的小矩形说明了什么
大部分居民的月均用水量都集中在什么之间
居民的月均用水量的分布呈“山峰”状的,而且是“单峰”的
另外还有一定的对称性.
月均用水量在[2,2.5)内的居民最多.
在[1,3)之间.
用水量/t
0.10
0.20
0.30
0.40
0.50
O
频率/组距
0.5
1
1.5
2.5
3.5
4.5
2
3
4
频率分布直方图的特征:
优点:从频率分布直方图可以清楚地看出数据分布的总体趋势
缺点:从频率分布直方图得不出原始的数据内容,把数据表示成直方图后,原有的具体数据就被抹掉了
如果当地政府希望85%以上的居民每月的用水量不超出标准,根据频率分布表和频率分布直方图,你能对制定月用水量提出建议吗
用水量/t
0.10
0.20
0.30
0.40
0.50
O
频率/组距
0.5
1
1.5
2.5
3.5
4.5
2
3
4
居民月用水量标准应定为3t.
分组 频数 频率 累积频率
[0,0.5) 4 0.04
[0.5,1) 8 0.08
[1,1.5) 15 0.15
[1.5,2) 22 0.22
[2,2.5) 25 0.25
[2.5,3) 14 0.14
[3,3.5) 6 0.06
[3.5,4) 4 0.04
[4,4.5) 2 0.02
合计 100 1.00
0.04
0.12
0.27
0.49
0.74
0.88
0.94
0.98
1.00
思考 你认为3吨这个标准一定能够保证85%以上的居民用水不超标吗?如果不一定,那么哪些环节可能导致结论的差别?
同样一组数据,如果组距不同,得到的图的形状也会不同。不同的形状给人以不同的印象,这种印象有时会影响我们对总体的判断。
抽查某地区55名12岁男生的身高(单位:cm)的测量值如下:
128.1 144.4 150.3 146.2 140.6 126.0 125.6 127.7 154.4 142.7 141.2 142.7 137.6 136.9 132.3 131.8 147.7 138.4 136.6 136.2 141.6 141.1 133.1 142.8 136.8 133.1 144.5 142.4 140.8 127.7 150.7 160.3 138.8 154.3 147.9 141.3 143.8 138.1 139.7 142.9 144.7 148.5 138.3 135.3 134.5 140.6 138.4 137.3 149.5 142.5 139.3 156.1 152.2 129.8 133.2
试从以上数据中,对该地区12岁男生的身高情况进行大致的推测。
为此,需要对统计数据进行整理和分析。分析数据的一种基本方法是用图将他们画出来,或用表格改变数据的排列方式。
1、求极差(最大值与最小值的差)
160.3-125.6=34.7
2、决定组距与组数(将数据分组)
组数=极差/组距=34.7/5≈6.9
因此组距为5,组数为7
3、将数据分组
4、画频率分布表
[125.45 ,130.45), [130.45, 135.45) ,[135.45, 140.45), [140.45, 145.45), [145.45, 150.45), [150.45,155.45) ,[155.45, 160.45]
分 组 频数 频率
[125.45 ,130.45) 6 0.109
[130.45, 135.45) 7 0.127
[135.45, 140.45) 14 0.255
[140.45, 145.45) 17 0.309
[145.45, 150.45) 5 0.091
[150.45, 155.45) 4 0.073
[155.45, 160.45] 2 0.036
合计 55 1.00
55名12岁男生身高的频率分布表
4、画频率分布表
5、画频率分布直方图
125.45 130.45
160.45
身高/cm
频率
组距
0.01
0.02
某地区为了了解知识分子的年龄结构,
随机抽样50名,其年龄分别如下:
42,38,29,36,41,43,54,43,34,44,
40,59,39,42,44,50,37,44,45,29,
48,45,53,48,37,28,46,50,37,44,
42,39,51,52,62,47,59,46,45,67,
53,49,65,47,54,63,57,43,46,58.
(1)列出样本频率分布表;
(2)画出频率分布直方图;
(3)估计年龄在32~52岁的知识分子所占的比例约是多少.
(1)极差为67-28=39,取组距为5,分为8组.
分 组 频数 频率
[27,32) 3 0.06
[32,37) 3 0.06
[37,42) 9 0.18
[42,47) 16 0.32
[47,52) 7 0.14
[52,57) 5 0.10
[57,62) 4 0.08
[62,67) 3 0.06
合 计 50 1.00
样本频率分布表:
(2)样本频率分布直方图:
年龄
0.06
0.05
0.04
0.03
0.02
0.01
27 32 37 42 47 52 57 62 67
频率
组距
O
(3)因为0.06+0.18+0.32+0.14=0.7, 故年龄在32~52岁的知识分子约占70%.
1. 右图是容量为100的样本的频率分布直方图,试根据图中的数据填空:
(1)样本数据落在范围[6,10)内的频率为____;
(2)样本数据落在范围[10,14)内的频数为____;
(3)总体在范围[2,6)内的概率约为_______;
O
2
6
10
14
18
0.02
0.03
0.08
0.09
样本数据
频率
组距
0.32
36
0.08
2.一个容量为35的样本,分组后,组距与频数如下:
[5,10)5,[10,15)12,[15,20)7,[20,25)5,[25,30)4,[30,35)2,则样本在区间[20,+∞)上的频率为( )
A.20% B.69% C.31% D.27%
C
3.一个容量为32的样本,已知某组样本的频率
为0.125,则该组样本的频数为( )
A.2 B.4 C.6 D.8
B
O
60
70
80
90
100
0.01
0.02
0.04
0.03
车速
频率
组距
110
4.某路段检查监控录象显示,在某时段内,有1000辆汽车通过该站,现在随机抽取其中的200辆汽车进行车速分析,则估计在这一时段内通过该站的汽车中速度不小于90km/h的约有( )
A100辆 B200辆
C300辆 D400辆
C
5.有一个容量为50的样本数据的分组的频数如下:
[12.5, 15.5) 3
[15.5, 18.5) 8
[18.5, 21.5) 9
[21.5, 24.5) 11
[24.5, 27.5) 10
[27.5, 30.5) 5
[30.5, 33.5 ] 4
(1)列出样本的频率分布表;
(2)画出频率分布直方图;
(3)根据频率分布直方图估计,数据落在[15.5, 24.5)的百分比是多少
0.040
0.010
0.030
频率
组距
解:组距为3
分组 频数 频率 频率/ 组距
0.06
0.16
0.18
0.22
0.20
0.10
0.08
1
0.020
0.053
0.060
0.073
0.067
0.033
0.027
[12.5, 15.5) 3
[15.5, 18.5) 8
[18.5, 21.5) 9
[21.5, 24.5) 11
[24.5, 27.5) 10
[27.5, 30.5) 5
[30.5, 33.5] 4
合计 50
0.020
0.050
12.5
15.5
0.060
0.070
18.5
27.5
21.5
24.5
33.5
30.5
数据落在[15.5, 24.5)
的百分比是56%
6、为了了解某地高一年级男生的身高情况,从其中的一个学校选取容量为60的样本(60名男生的身高,单位:cm),分组情况如下:
分组 151.5~158.5 158.5~165.5 165.5~172.5 172.5~179.5
频数 6 21 m
频率 a 0.1
则表中的m= , a=
6
0.45
27
频率分布直方图
应用
步骤
1.求极差
2.决定组距与组数
3.将数据分组
4.列频率分布表
5.画频率分布直方图
频率分布直方图各小长方形的面积表示相应各组的频率.这样,频率分布直方图就以面积的形式反映了数据落在各个小组的频率的大小.
2.2.1用样本的
频率分布估计总体分布
第一课时
我国是世界上严重缺水的国家之一,
城市缺水问题较为突出。
2000年全国主要城市中缺水情况排在前10位的城市
引入
政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a , 用水量不超过a的部分按平价收费,超过a的部分按议价收费。
①如果希望大部分居民的日常生活不受影响,那 么标准a定为多少比较合理呢?
②为了较合理地确定这个标准,你认为需要做
哪些工作?
这些数字告诉我们什么信息?
通过抽样,我们获得了100位居民某年的月平均用水量(单位:t) ,如下表:
3.1 2.5 2.0 2.0 1.5 1.0 1.6 1.8 1.9 1.6
3.4 2.6 2.2 2.2 1.5 1.2 0.2 0.4 0.3 0.4
3.2 2.7 2.3 2.1 1.6. 1.2 3.7 1.5 0.5 3.8
3.3 2.8 2.3 2.2 1.7 1.2 3.6 1.7 0.6 4.1
3.2 2.9 2.4 2.3 1.8 1.3 3.5 1.9 0.8 4.3
3.0 2.9 2.4 2.4 1.9 1.4 1.4 1.8 0.7 2.0
2.5 2.8 2.3 2.3 1.8 1.3 1.3 1.6 0.9 2.3
2.6 2.7 2.4 2.1 1.7 1.3 1.2 1.5 0.5 2.4
2.5 2.6 2.3 2.1 1.6 1.4 1.0 1.7 0.8 2.4
2.8 2.5 2.2 2.0 1.5 1.0 1.2 1.8 0.6 2.2
100位居民的月均用水量(单位:t)
从表中只能看出:最小值是0.2t,最大值是4.3t,其他的在0.2-4.3t之间.
分析数据的基本方法:
1.图(频率分布直方图)
2.表(频率分布表)
1.求极差(即一组数据中最大值与最小值的差)
2.决定组距与组数
4.3 - 0.2 = 4.1
4.1
0.5
= 8.2
组数=
组距
极差
=
3.将数据分组(左闭右开)
[0,0.5 ),[0.5,1 ),…,[4,4.5]
组数:将数据分组,当数据在100个以内时,
按数据多少常分5-12组。
组距:指每个小组的两个端点的距离,
4.列频率分布表
分组 频数累计 频数 频率
[0,0.5)
[0.5,1)
[1,1.5)
[1.5,2)
[2,2.5)
[2.5,3)
[3,3.5)
[3.5,4)
[4,4.5]
合计
4
8
15
22
25
14
6
4
2
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
100
1.00
频率=
样本容量
频数
频率分布表一般分“分组”,“频数累计”(可省),“频数”,“频率”, “频率/组距””五列,最后一行是合计
注意频数的合计应是样本容量,频率合计应是1
0.02
频率/组距
0.08
0.16
0.30
0.44
0.50
0.28
0.12
0.08
0.04
小矩形的面积
组距
频率
组距×
频率
=
=
分组 频数 频率 频率/组距
[0,0.5) 4 0.04 0.08
[0.5,1) 8 0.08 0.16
[1,1.5) 15 0.15 0.30
[1.5,2) 22 0.22 0.44
[2,2.5) 25 0.25 0.50
[2.5,3) 14 0.14 0.28
[3,3.5) 6 0.06 0.12
[3.5,4) 4 0.04 0.08
[4,4.5] 2 0.02 0.04
合计 100
5. 画频率分布直方图(与条形图区别):
用水量/t
0.10
0.20
0.30
0.40
0.50
O
频率/组距
0.5
1
1.5
2.5
3.5
4.5
2
3
4
请计算每个小矩形的面积,它代表什么 为什么
所有小矩形的面积的和是多少
1
注意
纵坐标是
频率/组距
用水量/t
0.10
0.20
0.30
0.40
0.50
O
频率/组距
0.5
1
1.5
2.5
3.5
4.5
2
3
4
频率分布直方图,显示了样本数据落在各个小组的比例的大小,图中最高的小矩形说明了什么
大部分居民的月均用水量都集中在什么之间
居民的月均用水量的分布呈“山峰”状的,而且是“单峰”的
另外还有一定的对称性.
月均用水量在[2,2.5)内的居民最多.
在[1,3)之间.
用水量/t
0.10
0.20
0.30
0.40
0.50
O
频率/组距
0.5
1
1.5
2.5
3.5
4.5
2
3
4
频率分布直方图的特征:
优点:从频率分布直方图可以清楚地看出数据分布的总体趋势
缺点:从频率分布直方图得不出原始的数据内容,把数据表示成直方图后,原有的具体数据就被抹掉了
如果当地政府希望85%以上的居民每月的用水量不超出标准,根据频率分布表和频率分布直方图,你能对制定月用水量提出建议吗
用水量/t
0.10
0.20
0.30
0.40
0.50
O
频率/组距
0.5
1
1.5
2.5
3.5
4.5
2
3
4
居民月用水量标准应定为3t.
分组 频数 频率 累积频率
[0,0.5) 4 0.04
[0.5,1) 8 0.08
[1,1.5) 15 0.15
[1.5,2) 22 0.22
[2,2.5) 25 0.25
[2.5,3) 14 0.14
[3,3.5) 6 0.06
[3.5,4) 4 0.04
[4,4.5) 2 0.02
合计 100 1.00
0.04
0.12
0.27
0.49
0.74
0.88
0.94
0.98
1.00
思考 你认为3吨这个标准一定能够保证85%以上的居民用水不超标吗?如果不一定,那么哪些环节可能导致结论的差别?
同样一组数据,如果组距不同,得到的图的形状也会不同。不同的形状给人以不同的印象,这种印象有时会影响我们对总体的判断。
抽查某地区55名12岁男生的身高(单位:cm)的测量值如下:
128.1 144.4 150.3 146.2 140.6 126.0 125.6 127.7 154.4 142.7 141.2 142.7 137.6 136.9 132.3 131.8 147.7 138.4 136.6 136.2 141.6 141.1 133.1 142.8 136.8 133.1 144.5 142.4 140.8 127.7 150.7 160.3 138.8 154.3 147.9 141.3 143.8 138.1 139.7 142.9 144.7 148.5 138.3 135.3 134.5 140.6 138.4 137.3 149.5 142.5 139.3 156.1 152.2 129.8 133.2
试从以上数据中,对该地区12岁男生的身高情况进行大致的推测。
为此,需要对统计数据进行整理和分析。分析数据的一种基本方法是用图将他们画出来,或用表格改变数据的排列方式。
1、求极差(最大值与最小值的差)
160.3-125.6=34.7
2、决定组距与组数(将数据分组)
组数=极差/组距=34.7/5≈6.9
因此组距为5,组数为7
3、将数据分组
4、画频率分布表
[125.45 ,130.45), [130.45, 135.45) ,[135.45, 140.45), [140.45, 145.45), [145.45, 150.45), [150.45,155.45) ,[155.45, 160.45]
分 组 频数 频率
[125.45 ,130.45) 6 0.109
[130.45, 135.45) 7 0.127
[135.45, 140.45) 14 0.255
[140.45, 145.45) 17 0.309
[145.45, 150.45) 5 0.091
[150.45, 155.45) 4 0.073
[155.45, 160.45] 2 0.036
合计 55 1.00
55名12岁男生身高的频率分布表
4、画频率分布表
5、画频率分布直方图
125.45 130.45
160.45
身高/cm
频率
组距
0.01
0.02
某地区为了了解知识分子的年龄结构,
随机抽样50名,其年龄分别如下:
42,38,29,36,41,43,54,43,34,44,
40,59,39,42,44,50,37,44,45,29,
48,45,53,48,37,28,46,50,37,44,
42,39,51,52,62,47,59,46,45,67,
53,49,65,47,54,63,57,43,46,58.
(1)列出样本频率分布表;
(2)画出频率分布直方图;
(3)估计年龄在32~52岁的知识分子所占的比例约是多少.
(1)极差为67-28=39,取组距为5,分为8组.
分 组 频数 频率
[27,32) 3 0.06
[32,37) 3 0.06
[37,42) 9 0.18
[42,47) 16 0.32
[47,52) 7 0.14
[52,57) 5 0.10
[57,62) 4 0.08
[62,67) 3 0.06
合 计 50 1.00
样本频率分布表:
(2)样本频率分布直方图:
年龄
0.06
0.05
0.04
0.03
0.02
0.01
27 32 37 42 47 52 57 62 67
频率
组距
O
(3)因为0.06+0.18+0.32+0.14=0.7, 故年龄在32~52岁的知识分子约占70%.
1. 右图是容量为100的样本的频率分布直方图,试根据图中的数据填空:
(1)样本数据落在范围[6,10)内的频率为____;
(2)样本数据落在范围[10,14)内的频数为____;
(3)总体在范围[2,6)内的概率约为_______;
O
2
6
10
14
18
0.02
0.03
0.08
0.09
样本数据
频率
组距
0.32
36
0.08
2.一个容量为35的样本,分组后,组距与频数如下:
[5,10)5,[10,15)12,[15,20)7,[20,25)5,[25,30)4,[30,35)2,则样本在区间[20,+∞)上的频率为( )
A.20% B.69% C.31% D.27%
C
3.一个容量为32的样本,已知某组样本的频率
为0.125,则该组样本的频数为( )
A.2 B.4 C.6 D.8
B
O
60
70
80
90
100
0.01
0.02
0.04
0.03
车速
频率
组距
110
4.某路段检查监控录象显示,在某时段内,有1000辆汽车通过该站,现在随机抽取其中的200辆汽车进行车速分析,则估计在这一时段内通过该站的汽车中速度不小于90km/h的约有( )
A100辆 B200辆
C300辆 D400辆
C
5.有一个容量为50的样本数据的分组的频数如下:
[12.5, 15.5) 3
[15.5, 18.5) 8
[18.5, 21.5) 9
[21.5, 24.5) 11
[24.5, 27.5) 10
[27.5, 30.5) 5
[30.5, 33.5 ] 4
(1)列出样本的频率分布表;
(2)画出频率分布直方图;
(3)根据频率分布直方图估计,数据落在[15.5, 24.5)的百分比是多少
0.040
0.010
0.030
频率
组距
解:组距为3
分组 频数 频率 频率/ 组距
0.06
0.16
0.18
0.22
0.20
0.10
0.08
1
0.020
0.053
0.060
0.073
0.067
0.033
0.027
[12.5, 15.5) 3
[15.5, 18.5) 8
[18.5, 21.5) 9
[21.5, 24.5) 11
[24.5, 27.5) 10
[27.5, 30.5) 5
[30.5, 33.5] 4
合计 50
0.020
0.050
12.5
15.5
0.060
0.070
18.5
27.5
21.5
24.5
33.5
30.5
数据落在[15.5, 24.5)
的百分比是56%
6、为了了解某地高一年级男生的身高情况,从其中的一个学校选取容量为60的样本(60名男生的身高,单位:cm),分组情况如下:
分组 151.5~158.5 158.5~165.5 165.5~172.5 172.5~179.5
频数 6 21 m
频率 a 0.1
则表中的m= , a=
6
0.45
27
频率分布直方图
应用
步骤
1.求极差
2.决定组距与组数
3.将数据分组
4.列频率分布表
5.画频率分布直方图
频率分布直方图各小长方形的面积表示相应各组的频率.这样,频率分布直方图就以面积的形式反映了数据落在各个小组的频率的大小.
