高中数学人教新课标B版必修3--《3.4 概率的应用》课件2(共36张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修3--《3.4 概率的应用》课件2(共36张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 14.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 00:00:00 | ||
图片预览











文档简介
(共36张PPT)
*
概率的应用
数 学
必修③ · 人教B版
新课标
处理有关概率应用问题时需要注意哪些方面
(1)处理概率的应用题要抓住关键词语,转化为数学问题.
(2)对一定数量的试验来说,事件发生的频率并不一定与概率完全相等.概率是频率的科学抽象,要通过大量重复试验来求得其近似值,因而概率是一个客观常数,它反映了随机事件的属性,如果一个事件是随机事件,即使该事件的概率再大,那么,在一次试验中,它可能发生,也可能不发生.
(3)用古典概型的观点求随机事件的概率时,首先是保证在试验中出现的结果的可能性是相等的,其次是通过一个比值的计算来确定随机事件的概率.
(4)在处理较复杂的问题时要注意事件的互斥性,合理运用概率的加法公式.
(5)几何概型的问题解决的关键是要构造出随机事件对应的几何图形,利用图形的几何度量来求随机事件的概率.
*
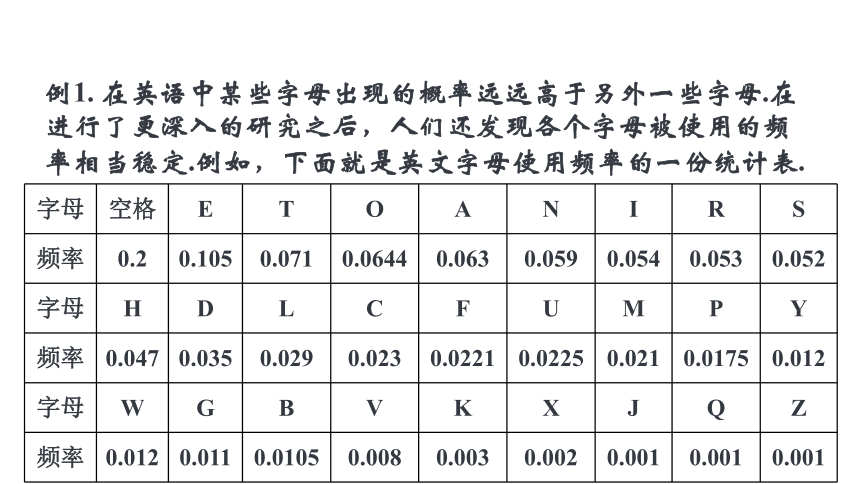
例1. 在英语中某些字母出现的概率远远高于另外一些字母.在进行了更深入的研究之后,人们还发现各个字母被使用的频率相当稳定.例如,下面就是英文字母使用频率的一份统计表.
字母 空格 E T O A N I R S
频率 0.2 0.105 0.071 0.0644 0.063 0.059 0.054 0.053 0.052
字母 H D L C F U M P Y
频率 0.047 0.035 0.029 0.023 0.0221 0.0225 0.021 0.0175 0.012
字母 W G B V K X J Q Z
频率 0.012 0.011 0.0105 0.008 0.003 0.002 0.001 0.001 0.001
从表中我们可以看出,空格的使用频率最高.有鉴于此,人们在设计键盘时,空格键不仅最大,而且放在使用方便的位置.
近年来对汉语的统计研究有了很大的发展.关于汉字的使用频率已有初步统计资料,对汉语常用词也作了一些统计研究.这些信息对汉字输入方案等的研制有很大帮助.使用过汉字拼音输入法的同学可能有体会.
如图,当输入拼音“shu”,则提示有以下几种可供选择:1.数,2.书,3.树,4.属,5.署……这个显示顺序基本上就是按照拼音为“shu”的汉字出现频率从大到小排列的.
数
▼ 1 数 2 书 3 树 4 属 5 署 6 输 7 淑 8 术 9 舒
例2. 在密码的编制和破译中,概率论起着重要的作用.要使敌人不能破译电文而又能使盟友容易译出电文,一直是外交官和将军们关心的问题.为了保密,通讯双方事先有一个秘密约定,称为密钥.发送信息方要把发出的真实信息——明文,按密钥规定,变成密文.接收方将密文按密钥还原成明文.
*
密码技术在军事、政治、经济方面有着广泛的用途.为了使密码设计更难破译,人们发明了许多反破译的方法,利用随机序列就是一种极为重要的方法,其原理是:利用取值在1到26之间的整数值随机数序列,使每个字母出现在密码中的概率都相等.
*
现代社会对破译密码的要求越来越高,有一种密码把英文的明文(真实文)按字母分解,其中英文的a,b,c,…,z的26个字母(不论大小写)依次对应1,2,3,…,26,这26个自然数,见表格:
a b c d e f g h i j k l m
1 2 3 4 5 6 7 8 9 10 11 12 13
n o p q r s t u v w x y z
14 15 16 17 18 19 20 21 22 23 24 25 26
*
*
试试破译下列密码:
L.dp.d.whdfkhu
最后答案是一句话
这是“凯撒移位密码”,字母按顺序往前3位移动,L往前3位是I,d往前3位是a,p往前3位是m ……以此类推。最后答案是 I am a teacher
例如,古罗马伟大的军事和政治家凯撒大帝把明文中的每个字母按拉丁字母次序后移三位之后的字母来代替,形成密文.接收方收到密文后,将每个字母前移三位后便得到明文. 这是一种原始的编制密码方法。
以传送命令:“We will start the fight at eleven O’ clock on Wednesday”为例,编译这个命令得到“Zh zloo vwduw wkh iljkw dw hohyhq r’ forfn rq Zhgqhvgdb”。
凯撒密码 (公元前一世纪)
被用于高卢战争
它是将英文字母向前推移k位。以此字母替代的密表,如k=5,则密文字母与明文与如下对应关系
a b c d e f g h i j k l m n o p q r s t u v w x y z
F G H I J K L M N O P Q R S T U V W X Y Z A B C D E
k就是最早的文字密钥
如果初次接触,会感到莫名其妙,不知如何是好。
这种方法使用了很长一段时间后,有人掌握了破译的方法。你知道是如何破译的吗?
在书面语言中单个的字母不是以同样的频率出现的.从例1中英文字母出现频率的统计表中我们可以看出,在英文常用文章中,平均说来出现字母“E”的频率约为10.5%, “T”约为7.1%,而“J”的出现远小于1%.
如果掌握了这个规律,再用上面的方法解密,通过对用密码写的密文中的字母进行频率分析,就能比较容易地破译出密文,出现频率最高的字母,无论你在编译中使用什么字母,它一般都表示“e”,出现频率次高的字母大概是“t”,等等。
现代保密系统采用了能确保每个字母出现在密文中的概率都相等的技术. 一种理论上不可破译的密码是“一次性密码本”(用后立即销毁). 这种密码本是一长串的随机数,每个都在1和26之间.这样一种密码本可能从以下数开始:19,7,12,1,3,8,…. 。
如“ELEVEN”这个词,用按字母表顺序排在E后面第19个字母表示E,而用L后面第7个字母表示L,等等.因此,ELEVEN变成了XSQWHV. 注意,尽管在明文中“E”出现3次,但是在密文XSQWHV中却是用三个不同的字母来替换的.
“二战”期间,为了加强对战机的防护,英美军方调查了作战后幸存飞机上弹痕的分布,决定哪里弹痕多就加强哪里。然而统计学家沃德力排众议,指出更应该注意弹痕少的部位,因为这些部位受到重创的战机,很难有机会返航,而这部分数据被忽略了。事实证明,沃德是正确的。
2018年高考全国II卷语文作文:
二战中,在铺天盖地的密集火网之下,战机机身上几乎所有的地方都可能挨炮弹,因此,需要用统计学来研究战机被击中的部位,并且从“幸存者偏差”倒推出需要加强防护的部位。
在二战期间,人们发现幸存的轰炸机中,机身中弹的数量很多,而机翼中弹的却很少。因此人们认为我们应该加固飞机的机身。其实不然,就是因为机身中弹多还能飞回来,所以机身中弹并没有影响飞机返航;而机翼中弹的少则说明了子弹打中机翼对飞机的影响更大,导致飞机不能返航。
举一个与之相同的例子,经过枪击案而活下来的人当中,手部和腿部中弹的居多,而击中头部和心脏的少之又少,正说明了人的头部和心脏对死亡率的影响更大而不是手和腿。
幸存者偏差意思是指,当取得资讯的渠道,仅来自于幸存者时(因为死人不会说话),此资讯可能会存在与实际情况不同的偏差。
此规律也适用于金融和商业领域。存活下来的企业往往被视为"传奇",它们的做法被争相效仿。而其实有些也许只是因为偶然原因幸存下来了而已。
在日常生活中,最明显的例子就是"我亲戚吃这个药好了"或者"我一个朋友去找了这个老中医"等等。不管你的亲戚和朋友和你关系如何好,如何值得信任和尊重,在客观规律面前他们都是等同的。疾病和医药不会因为你的喜好而照顾或者偏袒你的亲朋。
如何应对呢 最明显的办法当然是让"死人"说话。双盲实验设计和详细全面客观的数据纪录都是应对"幸存者偏差"的良方。所谓"兼听则明"也是这个道理,抛掉对个案的迷信,全面系统的了解才能克服这个偏差。
例3. 社会调查人员希望从人群的随机抽样调查中得到对他们所提问题诚实的回答.但是被采访者常常不愿意如实地作出应答.
1965年Stanley L. Warner发明了一种应用概率知识来消除这种不愿意情绪的方法. Warner的随机化应答方法要求人们随机地回答所提两个问题中的一个,而不必告诉采访者回答的是哪个问题. 两个问题中有一个是敏感的或者是令人为难的;另一个问题是无关紧要的. 这样应答者将乐意如实地回答问题,因为只有他知道自己回答的是哪个问题.
例如在调查运动员服用兴奋剂的时候,无关紧要的问题是“你的身份证号码的尾数是奇数吗”,敏感的问题是“你服用过兴奋剂吗”,然后要求被调查的运动员掷一枚硬币.如果出现正面,就回答第一个问题,否则回答第二个问题.
假如我们把这种方法用于200个被调查的运动员,得到54个“是”的回答.
因为掷硬币出现正面的概率为0.5,我们期望大约有100人回答了第一个问题.因为身份证号码尾数是奇数或偶数的可能性是同样的,因而在回答第一个问题的100人中大约有一半人,即50人,回答了“是”.其余4个回答“是”的人服用过兴奋剂. 由此我们估计这群人中大约有4%的人服用过兴奋剂 .
*
练习:
调查运动员服用兴奋剂的时候,应用Warner随机化方法调查300名运动员,得到80个“是”的回答,由此,我们估计服用过兴奋剂的人占这群人的( )
A.3.33% B.53% C.5% D.26%
例4. 为了估计水库中的鱼的尾数,可以使用以下的方法:先从水库中捕出一定数量的鱼,例如2000尾,给每尾鱼作上记号,不影响其存活,然后放回水库.经过适当的时间,让其和水库中其余的鱼充分混合,再从水库中捕出一定数量的鱼,例如500尾,查看其中有记号的鱼,设有40尾. 试根据上述数据,估计水库内鱼的尾数.
解:设水库中鱼的尾数为n,从水库中任捕一尾,每尾鱼被捕的频率(代替概率)为 ,第二次从水库中捕出500尾,带有记号的鱼有40尾,则带记号的鱼被捕的频率(代替概率) 为
则
解得n≈25000.
所以水库中约有鱼25000尾 .
练习:
为了估计某自然保护区中天鹅的数量,可以使用以下方法:先从该保护区中捕出一定数量的天鹅,例如200只,给每只天鹅做上记号,不影响其存活,然后放回保护区,经过适当的时间,让其和保护区中其余的天鹅充分混合,再从保护区中捕出一定数量的天鹅,例如150只,查看其中有记号的天鹅,设有20只,试根据上述数据,估计该自然保护区中天鹅的数量.
课堂小结
*
概率的应用
数 学
必修③ · 人教B版
新课标
处理有关概率应用问题时需要注意哪些方面
(1)处理概率的应用题要抓住关键词语,转化为数学问题.
(2)对一定数量的试验来说,事件发生的频率并不一定与概率完全相等.概率是频率的科学抽象,要通过大量重复试验来求得其近似值,因而概率是一个客观常数,它反映了随机事件的属性,如果一个事件是随机事件,即使该事件的概率再大,那么,在一次试验中,它可能发生,也可能不发生.
(3)用古典概型的观点求随机事件的概率时,首先是保证在试验中出现的结果的可能性是相等的,其次是通过一个比值的计算来确定随机事件的概率.
(4)在处理较复杂的问题时要注意事件的互斥性,合理运用概率的加法公式.
(5)几何概型的问题解决的关键是要构造出随机事件对应的几何图形,利用图形的几何度量来求随机事件的概率.
*
例1. 在英语中某些字母出现的概率远远高于另外一些字母.在进行了更深入的研究之后,人们还发现各个字母被使用的频率相当稳定.例如,下面就是英文字母使用频率的一份统计表.
字母 空格 E T O A N I R S
频率 0.2 0.105 0.071 0.0644 0.063 0.059 0.054 0.053 0.052
字母 H D L C F U M P Y
频率 0.047 0.035 0.029 0.023 0.0221 0.0225 0.021 0.0175 0.012
字母 W G B V K X J Q Z
频率 0.012 0.011 0.0105 0.008 0.003 0.002 0.001 0.001 0.001
从表中我们可以看出,空格的使用频率最高.有鉴于此,人们在设计键盘时,空格键不仅最大,而且放在使用方便的位置.
近年来对汉语的统计研究有了很大的发展.关于汉字的使用频率已有初步统计资料,对汉语常用词也作了一些统计研究.这些信息对汉字输入方案等的研制有很大帮助.使用过汉字拼音输入法的同学可能有体会.
如图,当输入拼音“shu”,则提示有以下几种可供选择:1.数,2.书,3.树,4.属,5.署……这个显示顺序基本上就是按照拼音为“shu”的汉字出现频率从大到小排列的.
数
▼ 1 数 2 书 3 树 4 属 5 署 6 输 7 淑 8 术 9 舒
例2. 在密码的编制和破译中,概率论起着重要的作用.要使敌人不能破译电文而又能使盟友容易译出电文,一直是外交官和将军们关心的问题.为了保密,通讯双方事先有一个秘密约定,称为密钥.发送信息方要把发出的真实信息——明文,按密钥规定,变成密文.接收方将密文按密钥还原成明文.
*
密码技术在军事、政治、经济方面有着广泛的用途.为了使密码设计更难破译,人们发明了许多反破译的方法,利用随机序列就是一种极为重要的方法,其原理是:利用取值在1到26之间的整数值随机数序列,使每个字母出现在密码中的概率都相等.
*
现代社会对破译密码的要求越来越高,有一种密码把英文的明文(真实文)按字母分解,其中英文的a,b,c,…,z的26个字母(不论大小写)依次对应1,2,3,…,26,这26个自然数,见表格:
a b c d e f g h i j k l m
1 2 3 4 5 6 7 8 9 10 11 12 13
n o p q r s t u v w x y z
14 15 16 17 18 19 20 21 22 23 24 25 26
*
*
试试破译下列密码:
L.dp.d.whdfkhu
最后答案是一句话
这是“凯撒移位密码”,字母按顺序往前3位移动,L往前3位是I,d往前3位是a,p往前3位是m ……以此类推。最后答案是 I am a teacher
例如,古罗马伟大的军事和政治家凯撒大帝把明文中的每个字母按拉丁字母次序后移三位之后的字母来代替,形成密文.接收方收到密文后,将每个字母前移三位后便得到明文. 这是一种原始的编制密码方法。
以传送命令:“We will start the fight at eleven O’ clock on Wednesday”为例,编译这个命令得到“Zh zloo vwduw wkh iljkw dw hohyhq r’ forfn rq Zhgqhvgdb”。
凯撒密码 (公元前一世纪)
被用于高卢战争
它是将英文字母向前推移k位。以此字母替代的密表,如k=5,则密文字母与明文与如下对应关系
a b c d e f g h i j k l m n o p q r s t u v w x y z
F G H I J K L M N O P Q R S T U V W X Y Z A B C D E
k就是最早的文字密钥
如果初次接触,会感到莫名其妙,不知如何是好。
这种方法使用了很长一段时间后,有人掌握了破译的方法。你知道是如何破译的吗?
在书面语言中单个的字母不是以同样的频率出现的.从例1中英文字母出现频率的统计表中我们可以看出,在英文常用文章中,平均说来出现字母“E”的频率约为10.5%, “T”约为7.1%,而“J”的出现远小于1%.
如果掌握了这个规律,再用上面的方法解密,通过对用密码写的密文中的字母进行频率分析,就能比较容易地破译出密文,出现频率最高的字母,无论你在编译中使用什么字母,它一般都表示“e”,出现频率次高的字母大概是“t”,等等。
现代保密系统采用了能确保每个字母出现在密文中的概率都相等的技术. 一种理论上不可破译的密码是“一次性密码本”(用后立即销毁). 这种密码本是一长串的随机数,每个都在1和26之间.这样一种密码本可能从以下数开始:19,7,12,1,3,8,…. 。
如“ELEVEN”这个词,用按字母表顺序排在E后面第19个字母表示E,而用L后面第7个字母表示L,等等.因此,ELEVEN变成了XSQWHV. 注意,尽管在明文中“E”出现3次,但是在密文XSQWHV中却是用三个不同的字母来替换的.
“二战”期间,为了加强对战机的防护,英美军方调查了作战后幸存飞机上弹痕的分布,决定哪里弹痕多就加强哪里。然而统计学家沃德力排众议,指出更应该注意弹痕少的部位,因为这些部位受到重创的战机,很难有机会返航,而这部分数据被忽略了。事实证明,沃德是正确的。
2018年高考全国II卷语文作文:
二战中,在铺天盖地的密集火网之下,战机机身上几乎所有的地方都可能挨炮弹,因此,需要用统计学来研究战机被击中的部位,并且从“幸存者偏差”倒推出需要加强防护的部位。
在二战期间,人们发现幸存的轰炸机中,机身中弹的数量很多,而机翼中弹的却很少。因此人们认为我们应该加固飞机的机身。其实不然,就是因为机身中弹多还能飞回来,所以机身中弹并没有影响飞机返航;而机翼中弹的少则说明了子弹打中机翼对飞机的影响更大,导致飞机不能返航。
举一个与之相同的例子,经过枪击案而活下来的人当中,手部和腿部中弹的居多,而击中头部和心脏的少之又少,正说明了人的头部和心脏对死亡率的影响更大而不是手和腿。
幸存者偏差意思是指,当取得资讯的渠道,仅来自于幸存者时(因为死人不会说话),此资讯可能会存在与实际情况不同的偏差。
此规律也适用于金融和商业领域。存活下来的企业往往被视为"传奇",它们的做法被争相效仿。而其实有些也许只是因为偶然原因幸存下来了而已。
在日常生活中,最明显的例子就是"我亲戚吃这个药好了"或者"我一个朋友去找了这个老中医"等等。不管你的亲戚和朋友和你关系如何好,如何值得信任和尊重,在客观规律面前他们都是等同的。疾病和医药不会因为你的喜好而照顾或者偏袒你的亲朋。
如何应对呢 最明显的办法当然是让"死人"说话。双盲实验设计和详细全面客观的数据纪录都是应对"幸存者偏差"的良方。所谓"兼听则明"也是这个道理,抛掉对个案的迷信,全面系统的了解才能克服这个偏差。
例3. 社会调查人员希望从人群的随机抽样调查中得到对他们所提问题诚实的回答.但是被采访者常常不愿意如实地作出应答.
1965年Stanley L. Warner发明了一种应用概率知识来消除这种不愿意情绪的方法. Warner的随机化应答方法要求人们随机地回答所提两个问题中的一个,而不必告诉采访者回答的是哪个问题. 两个问题中有一个是敏感的或者是令人为难的;另一个问题是无关紧要的. 这样应答者将乐意如实地回答问题,因为只有他知道自己回答的是哪个问题.
例如在调查运动员服用兴奋剂的时候,无关紧要的问题是“你的身份证号码的尾数是奇数吗”,敏感的问题是“你服用过兴奋剂吗”,然后要求被调查的运动员掷一枚硬币.如果出现正面,就回答第一个问题,否则回答第二个问题.
假如我们把这种方法用于200个被调查的运动员,得到54个“是”的回答.
因为掷硬币出现正面的概率为0.5,我们期望大约有100人回答了第一个问题.因为身份证号码尾数是奇数或偶数的可能性是同样的,因而在回答第一个问题的100人中大约有一半人,即50人,回答了“是”.其余4个回答“是”的人服用过兴奋剂. 由此我们估计这群人中大约有4%的人服用过兴奋剂 .
*
练习:
调查运动员服用兴奋剂的时候,应用Warner随机化方法调查300名运动员,得到80个“是”的回答,由此,我们估计服用过兴奋剂的人占这群人的( )
A.3.33% B.53% C.5% D.26%
例4. 为了估计水库中的鱼的尾数,可以使用以下的方法:先从水库中捕出一定数量的鱼,例如2000尾,给每尾鱼作上记号,不影响其存活,然后放回水库.经过适当的时间,让其和水库中其余的鱼充分混合,再从水库中捕出一定数量的鱼,例如500尾,查看其中有记号的鱼,设有40尾. 试根据上述数据,估计水库内鱼的尾数.
解:设水库中鱼的尾数为n,从水库中任捕一尾,每尾鱼被捕的频率(代替概率)为 ,第二次从水库中捕出500尾,带有记号的鱼有40尾,则带记号的鱼被捕的频率(代替概率) 为
则
解得n≈25000.
所以水库中约有鱼25000尾 .
练习:
为了估计某自然保护区中天鹅的数量,可以使用以下方法:先从该保护区中捕出一定数量的天鹅,例如200只,给每只天鹅做上记号,不影响其存活,然后放回保护区,经过适当的时间,让其和保护区中其余的天鹅充分混合,再从保护区中捕出一定数量的天鹅,例如150只,查看其中有记号的天鹅,设有20只,试根据上述数据,估计该自然保护区中天鹅的数量.
课堂小结
