数学人教A版(2019)必修第二册8.1.2旋转体(共21张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册8.1.2旋转体(共21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 689.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 21:20:32 | ||
图片预览


文档简介
(共21张PPT)
8.1 基本立体图形(第2课时)
第八章 立体几何初步
人教A版2019必修第二册
温故知新
1.棱柱的概念:
一个多面体有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互相平行,这样的多面体叫做棱柱
2.棱锥定义
一般地,有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥
3、棱台的概念:用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分叫做棱台。
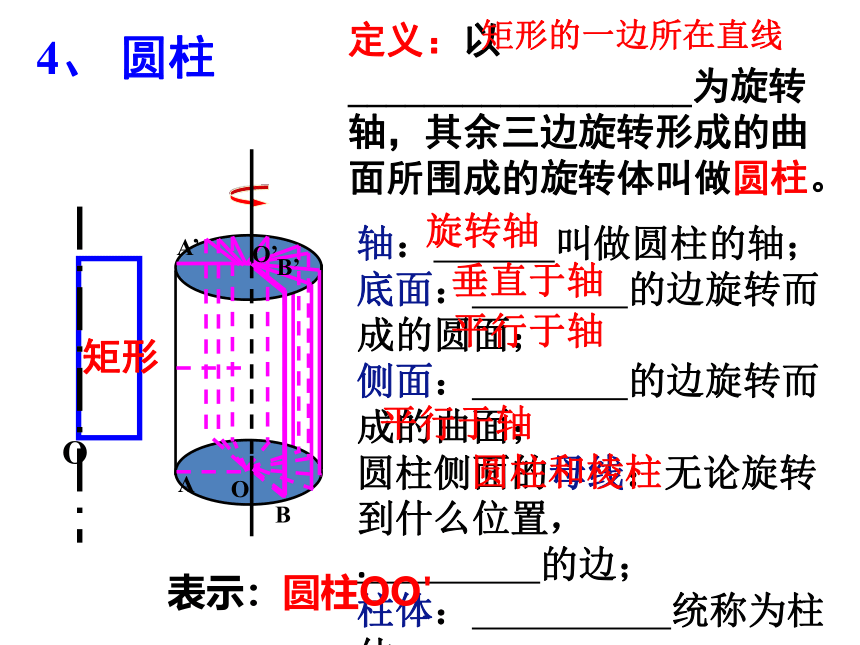
轴: 叫做圆柱的轴;
底面: 的边旋转而成的圆面;
侧面: 的边旋转而成的曲面;
圆柱侧面的母线:无论旋转到什么位置,
. 的边;
柱体: 统称为柱体.
4、 圆柱
矩形
O
A’
B’
A
O
B
O’
定义:以__________________为旋转轴,其余三边旋转形成的曲面所围成的旋转体叫做圆柱。
矩形的一边所在直线
旋转轴
垂直于轴
平行于轴
平行于轴
圆柱和棱柱
表示:圆柱OO'
A
A′
O
O′
旋转轴
底面
母线
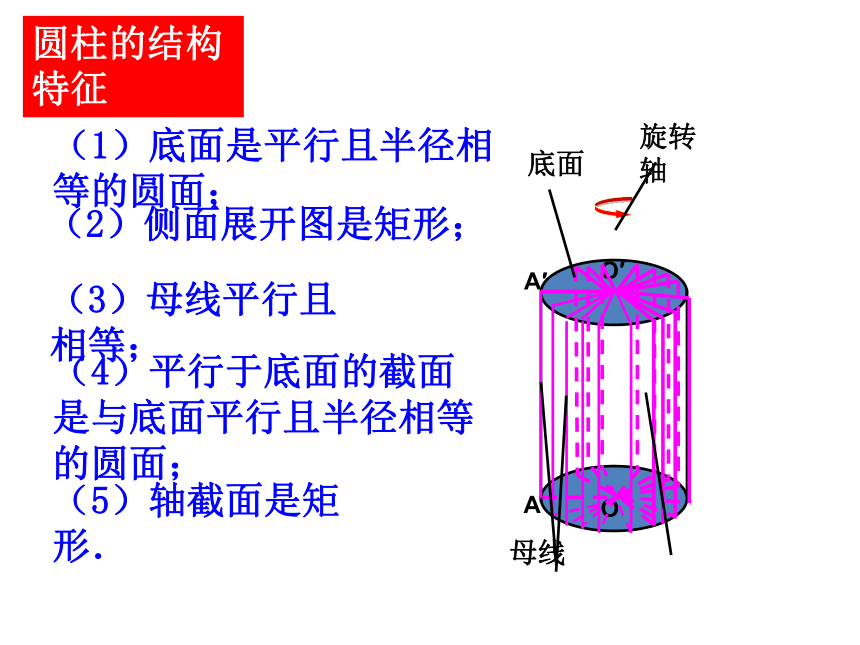
(1)底面是平行且半径相等的圆面;
(2)侧面展开图是矩形;
(3)母线平行且相等;
(4)平行于底面的截面是与底面平行且半径相等的圆面;
(5)轴截面是矩形.
圆柱的结构特征
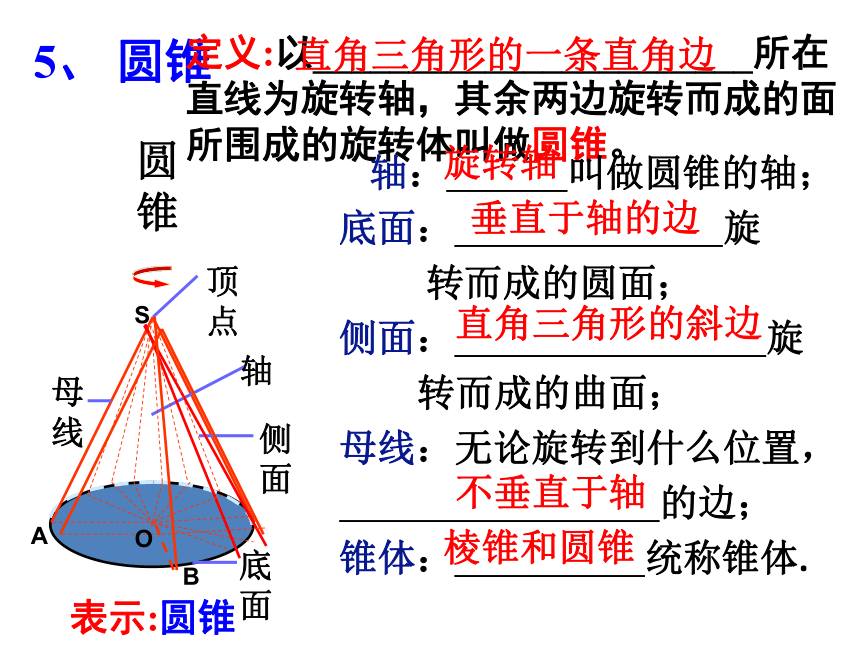
5、 圆锥
定义:以_______________________所在直线为旋转轴,其余两边旋转而成的面所围成的旋转体叫做圆锥。
直角三角形的一条直角边
圆锥
顶点
A
B
底面
轴
侧面
母线
S
O
轴: 叫做圆锥的轴;
底面: 旋
转而成的圆面;
侧面: 旋
转而成的曲面;
母线:无论旋转到什么位置,
的边;
锥体: 统称锥体.
旋转轴
垂直于轴的边
直角三角形的斜边
不垂直于轴
棱锥和圆锥
表示:圆锥SO
圆锥
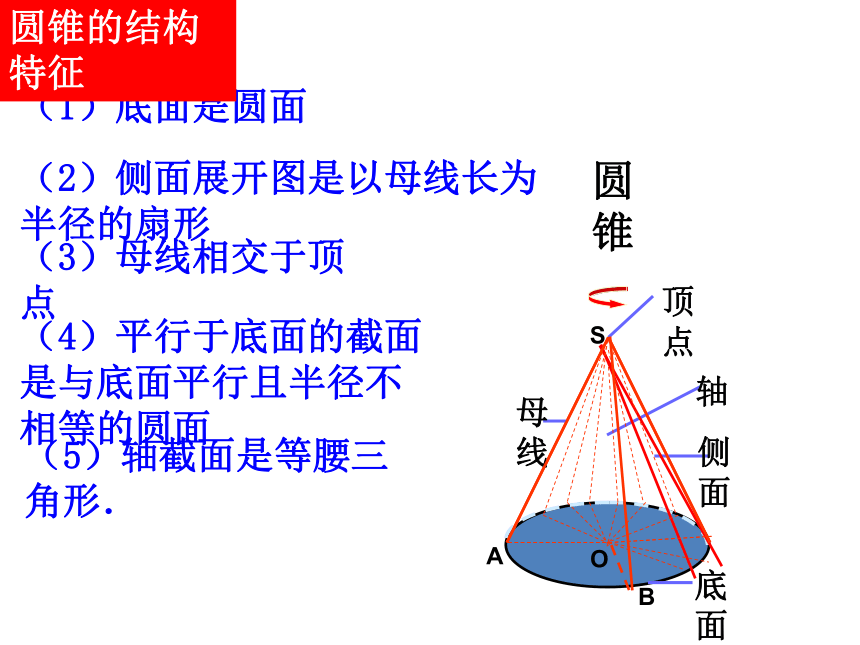
(1)底面是圆面
(2)侧面展开图是以母线长为半径的扇形
(3)母线相交于顶点
(4)平行于底面的截面是与底面平行且半径不相等的圆面
(5)轴截面是等腰三角形.
顶点
A
B
底面
轴
侧面
母线
S
O
圆锥的结构特征
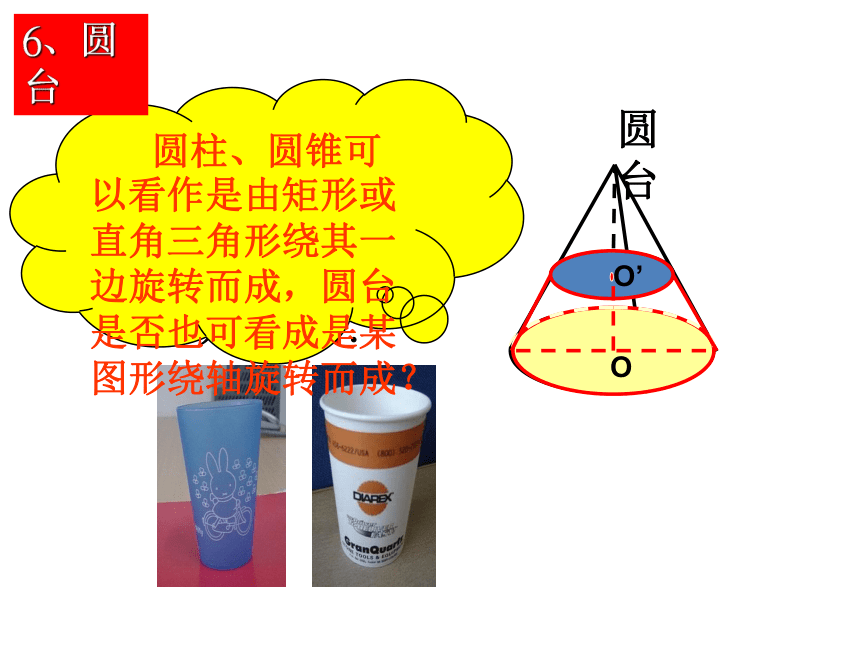
用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分是圆台.
圆台
O
O’
圆柱、圆锥可以看作是由矩形或直角三角形绕其一边旋转而成,圆台是否也可看成是某图形绕轴旋转而成?
6、圆台
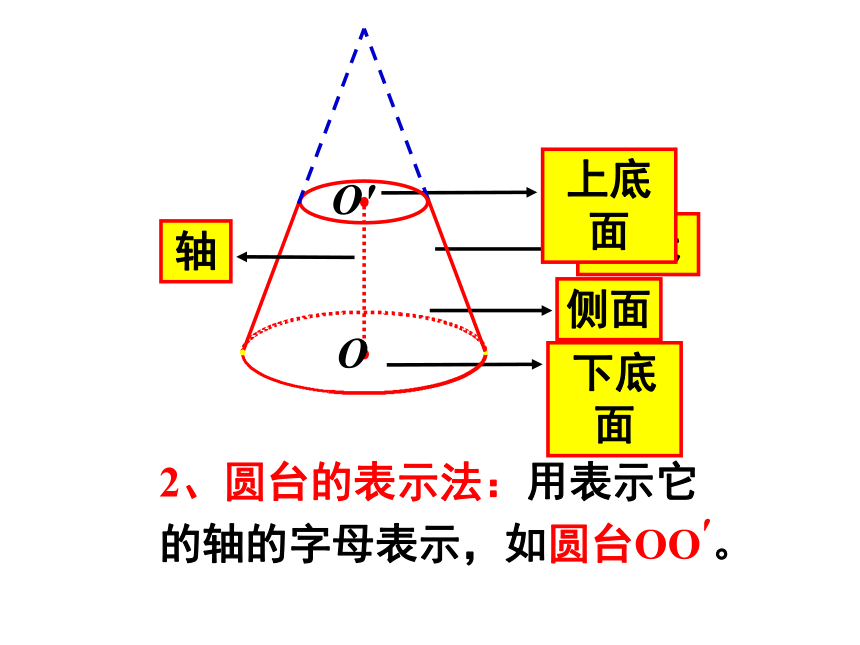
侧面
母线
上底面
下底面
O
O'
轴
2、圆台的表示法:用表示它的轴的字母表示,如圆台OO′。
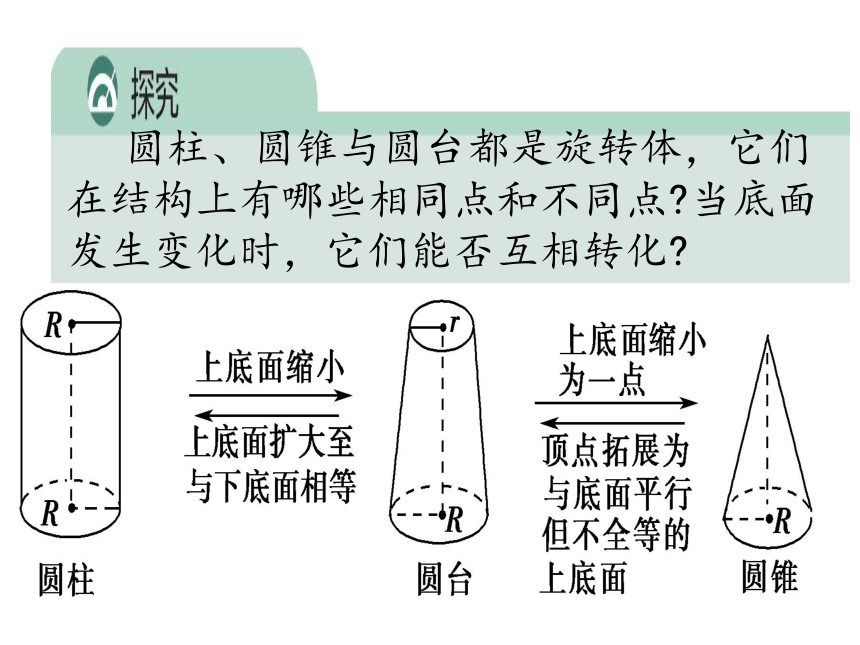
圆柱、圆锥与圆台都是旋转体,它们在结构上有哪些相同点和不同点 当底面发生变化时,它们能否互相转化
7、球的结构特征:
定义:以____________所在直线为旋转轴,半圆面旋转一周形成的几何体,叫做球体。
O
A
B
半径
球心
表示:球O
半圆的直径
球心:半圆的 叫做球的球心;
半径:连接 的
线段叫做球的半径;
直径:连接球面上两点并且经
过 的线段叫做球的直径.
圆心
球心和球面上任意一点
球心
思考:用一个平面去截一个球,截面是什么
O
用一个截面去截一个球,截面是圆面。
球面被经过球心的平面截得的圆叫做大圆。
球面被不过球心的平面截得的圆叫做小圆。
球、圆柱、圆锥、圆台过轴的截面分别是什么图形
想一想:
思考题:1.平行于圆柱,圆锥,圆台的底面的
截面是什么图形?
2.过圆柱,圆锥,圆台的旋转轴的截
面是什么图形?
性质1:平行于底面的截面都是圆面。
性质2:过轴的截面(轴截面)分别是
全等的矩形,等腰三角形,等腰梯形。
日常生活中常用到的日用品,比如:消毒液、暖瓶、洗洁精等的主要几何结构特征是什么?
圆柱
圆台
圆柱
8、简单组合体的结构特征:
简单组合体的结构特征:
1、简单组合体的定义: .2、简单组合体的两种基本形式:
①由简单几何体 而成;
②由简单几何体 一部分而成.
由简单几何体组合而成的几何体
拼接
截去或挖去
····························例1 给出下列说法:(1)圆柱的底面是圆面;(2)经过圆柱任意两条母线的截面是一个矩形面;(3)圆台的任意两条母线的延长线可能相交,也可能不相交;(4)夹在圆柱的两个截面间的几何体还是一个旋转体.
其中说法正确的是_______
跟踪训练一判断下列各命题是否正确.(1)一直角梯形绕下底所在直线旋转一周,所形成的曲面围成的几何体是圆台;(2)圆锥、圆台中过轴的截面是轴截面,圆锥的轴截面是等腰三角形,圆台的轴截面是等腰梯形;(3)到定点的距离等于定长的点的集合是球.
题型一 旋转体的结构特点
例2 观察下列几何体的结构特征,完成以下问题:
(1)几何体①是由哪些简单几何体构成的?试画出几何图形,使得旋转该图形180°后得到几何体①.(2)几何体②的结构特点是什么?试画出几何图形,使得旋转该图形360°得到几何体②.(3)几何体③是由哪些简单几何体构成的?并说明该几何体的面数、棱数、顶点数.
题型二 简单组合体
跟踪训练二下列组合体是由哪些几何体组成的?
例3 已知球的半径为10 cm,若它的一个截面圆的面积为36π cm2,则球心与截面圆圆心的距离是________ cm.
例4 如图,底面半径为1,高为2的圆柱,在A点有一只蚂蚁,现在这只蚂蚁要围绕圆柱由A点爬到B点,问蚂蚁爬行的最短距离是多少?
题型三 旋转体的有关计算
跟踪训练三
如图,圆台侧面的母线AB的长为20 cm,上、下底面的半径分别为5 cm,10 cm,从母线AB的中点M处拉一条绳子绕圆台侧面转到B点,求这条绳子长度的最小值.
课堂小结
1
简单空间几何体的分类:
简单的几何体
柱体
锥体
台体
圆柱
棱柱
圆锥
棱锥
2
3
5
4
6
7
球体
圆台
棱台
多面体:把由若干个平面多边形围成的几何体叫做多面体.
旋转体:把由一个平面图形绕它所在平面内的一条直线旋转所形成的封闭几何体叫做旋转体,这条定直线叫做旋转体的轴.
(1)(2)(3)(5)一类
(4)(6)(7)一类
生活中的立体图形
8.1 基本立体图形(第2课时)
第八章 立体几何初步
人教A版2019必修第二册
温故知新
1.棱柱的概念:
一个多面体有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互相平行,这样的多面体叫做棱柱
2.棱锥定义
一般地,有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥
3、棱台的概念:用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分叫做棱台。
轴: 叫做圆柱的轴;
底面: 的边旋转而成的圆面;
侧面: 的边旋转而成的曲面;
圆柱侧面的母线:无论旋转到什么位置,
. 的边;
柱体: 统称为柱体.
4、 圆柱
矩形
O
A’
B’
A
O
B
O’
定义:以__________________为旋转轴,其余三边旋转形成的曲面所围成的旋转体叫做圆柱。
矩形的一边所在直线
旋转轴
垂直于轴
平行于轴
平行于轴
圆柱和棱柱
表示:圆柱OO'
A
A′
O
O′
旋转轴
底面
母线
(1)底面是平行且半径相等的圆面;
(2)侧面展开图是矩形;
(3)母线平行且相等;
(4)平行于底面的截面是与底面平行且半径相等的圆面;
(5)轴截面是矩形.
圆柱的结构特征
5、 圆锥
定义:以_______________________所在直线为旋转轴,其余两边旋转而成的面所围成的旋转体叫做圆锥。
直角三角形的一条直角边
圆锥
顶点
A
B
底面
轴
侧面
母线
S
O
轴: 叫做圆锥的轴;
底面: 旋
转而成的圆面;
侧面: 旋
转而成的曲面;
母线:无论旋转到什么位置,
的边;
锥体: 统称锥体.
旋转轴
垂直于轴的边
直角三角形的斜边
不垂直于轴
棱锥和圆锥
表示:圆锥SO
圆锥
(1)底面是圆面
(2)侧面展开图是以母线长为半径的扇形
(3)母线相交于顶点
(4)平行于底面的截面是与底面平行且半径不相等的圆面
(5)轴截面是等腰三角形.
顶点
A
B
底面
轴
侧面
母线
S
O
圆锥的结构特征
用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分是圆台.
圆台
O
O’
圆柱、圆锥可以看作是由矩形或直角三角形绕其一边旋转而成,圆台是否也可看成是某图形绕轴旋转而成?
6、圆台
侧面
母线
上底面
下底面
O
O'
轴
2、圆台的表示法:用表示它的轴的字母表示,如圆台OO′。
圆柱、圆锥与圆台都是旋转体,它们在结构上有哪些相同点和不同点 当底面发生变化时,它们能否互相转化
7、球的结构特征:
定义:以____________所在直线为旋转轴,半圆面旋转一周形成的几何体,叫做球体。
O
A
B
半径
球心
表示:球O
半圆的直径
球心:半圆的 叫做球的球心;
半径:连接 的
线段叫做球的半径;
直径:连接球面上两点并且经
过 的线段叫做球的直径.
圆心
球心和球面上任意一点
球心
思考:用一个平面去截一个球,截面是什么
O
用一个截面去截一个球,截面是圆面。
球面被经过球心的平面截得的圆叫做大圆。
球面被不过球心的平面截得的圆叫做小圆。
球、圆柱、圆锥、圆台过轴的截面分别是什么图形
想一想:
思考题:1.平行于圆柱,圆锥,圆台的底面的
截面是什么图形?
2.过圆柱,圆锥,圆台的旋转轴的截
面是什么图形?
性质1:平行于底面的截面都是圆面。
性质2:过轴的截面(轴截面)分别是
全等的矩形,等腰三角形,等腰梯形。
日常生活中常用到的日用品,比如:消毒液、暖瓶、洗洁精等的主要几何结构特征是什么?
圆柱
圆台
圆柱
8、简单组合体的结构特征:
简单组合体的结构特征:
1、简单组合体的定义: .2、简单组合体的两种基本形式:
①由简单几何体 而成;
②由简单几何体 一部分而成.
由简单几何体组合而成的几何体
拼接
截去或挖去
····························例1 给出下列说法:(1)圆柱的底面是圆面;(2)经过圆柱任意两条母线的截面是一个矩形面;(3)圆台的任意两条母线的延长线可能相交,也可能不相交;(4)夹在圆柱的两个截面间的几何体还是一个旋转体.
其中说法正确的是_______
跟踪训练一判断下列各命题是否正确.(1)一直角梯形绕下底所在直线旋转一周,所形成的曲面围成的几何体是圆台;(2)圆锥、圆台中过轴的截面是轴截面,圆锥的轴截面是等腰三角形,圆台的轴截面是等腰梯形;(3)到定点的距离等于定长的点的集合是球.
题型一 旋转体的结构特点
例2 观察下列几何体的结构特征,完成以下问题:
(1)几何体①是由哪些简单几何体构成的?试画出几何图形,使得旋转该图形180°后得到几何体①.(2)几何体②的结构特点是什么?试画出几何图形,使得旋转该图形360°得到几何体②.(3)几何体③是由哪些简单几何体构成的?并说明该几何体的面数、棱数、顶点数.
题型二 简单组合体
跟踪训练二下列组合体是由哪些几何体组成的?
例3 已知球的半径为10 cm,若它的一个截面圆的面积为36π cm2,则球心与截面圆圆心的距离是________ cm.
例4 如图,底面半径为1,高为2的圆柱,在A点有一只蚂蚁,现在这只蚂蚁要围绕圆柱由A点爬到B点,问蚂蚁爬行的最短距离是多少?
题型三 旋转体的有关计算
跟踪训练三
如图,圆台侧面的母线AB的长为20 cm,上、下底面的半径分别为5 cm,10 cm,从母线AB的中点M处拉一条绳子绕圆台侧面转到B点,求这条绳子长度的最小值.
课堂小结
1
简单空间几何体的分类:
简单的几何体
柱体
锥体
台体
圆柱
棱柱
圆锥
棱锥
2
3
5
4
6
7
球体
圆台
棱台
多面体:把由若干个平面多边形围成的几何体叫做多面体.
旋转体:把由一个平面图形绕它所在平面内的一条直线旋转所形成的封闭几何体叫做旋转体,这条定直线叫做旋转体的轴.
(1)(2)(3)(5)一类
(4)(6)(7)一类
生活中的立体图形
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
