数学人教A版(2019)选择性必修第一册1.4空间向量的应用(共40张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.4空间向量的应用(共40张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 21:21:46 | ||
图片预览







文档简介
(共40张PPT)
1.4 空间向量的应用
第一章 空间向量与立体几何
目录
二、知识讲解
三、小结
四、练习
一、上节回溯
五、本章知识结构
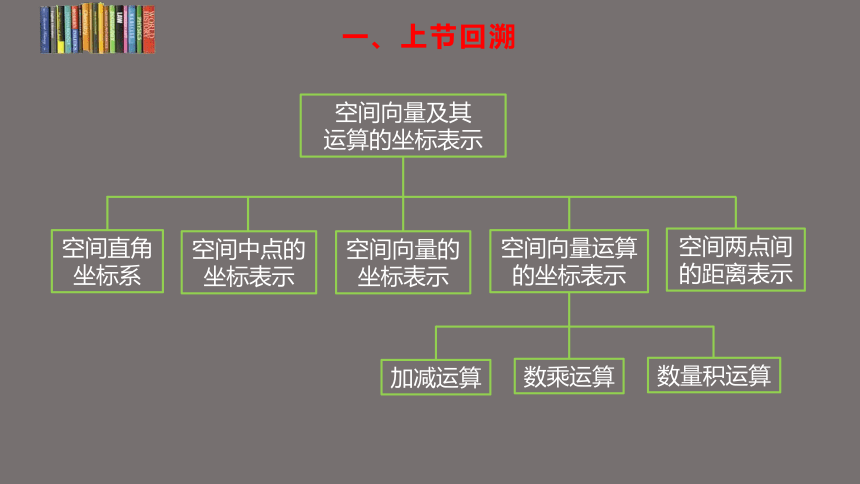
一、上节回溯
空间向量及其
运算的坐标表示
空间直角
坐标系
空间中点的坐标表示
空间两点间的距离表示
空间向量的坐标表示
空间向量运算的坐标表示
数乘运算
加减运算
数量积运算
1.空间中点、直线和平面的向量表示
二、知识讲解
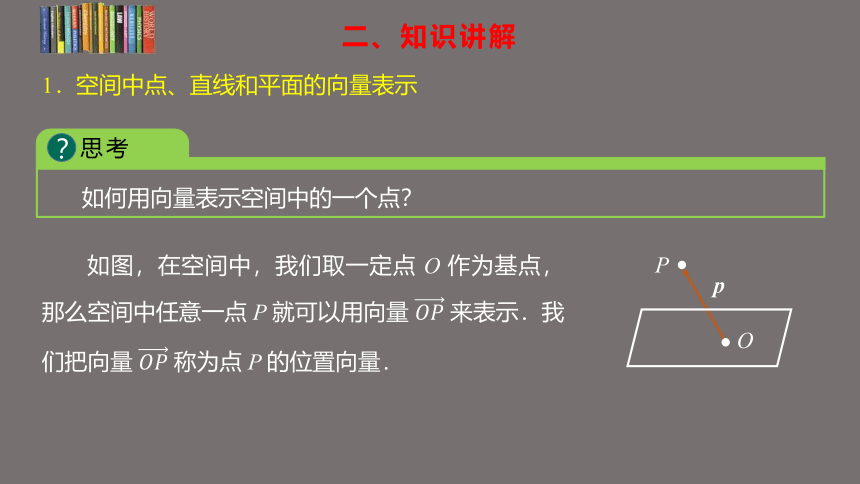
如何用向量表示空间中的一个点?
?
思考
如图,在空间中,我们取一定点 O 作为基点,那么空间中任意一点 P 就可以用向量 来表示.我们把向量 称为点 P 的位置向量.
P
p
O
二、知识讲解
我们知道,空间中给定一个点 A 和一个方向就能唯一确定一条直线 l.如何用向量表示直线 l ?
?
思考
如图,a是直线 l 的方向向量,在直线 l 上取 =a,设 P是直线 l 上的任意一点,由向量共线的条件可知,点 P 在直线 l 上的充要条件是存在实数 t,使得
=ta,即 =t.
a
A
P
B
l
1.空间中点、直线和平面的向量表示
二、知识讲解
你能证明这个结论吗?
?
进一步地,如图,取定空间中的任意一点 O,可以得到点 P 在直线 l 上的充要条件是存在实数 t,使
=+ta, ①
将 =a 代入 ①式,得
=+t. ②
① 式和 ②式都称为空间直线的向量表示式.由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.
a
A
P
B
l
O
1.空间中点、直线和平面的向量表示
二、知识讲解
一个定点和两个定方向能否确定一个平面?进一步地,一个定点和一个定方向能否确定一个平面?如果能确定,如何用向量表示这个平面?
?
思考
我们知道,平面 α可以由 α内两条相交直线确定.如图,设两条直线相交于点 O,它们的方向向量分别为 a和 b,P为平面 α内任意一点,由平面向量基本定理可知,存在唯一的有序实数对 (x,y),使得 =xa+yb .
P
b
O
a
α
1.空间中点、直线和平面的向量表示
二、知识讲解
进一步地,如图,取定空间任意一点 O,可以得到,空间一点 P 位于平面 ABC 内的充要条件是存在实数 x,y,使
=+x+y.③
我们把 ③式称为空间平面 ABC 的向量表示式.由此可知,空间中任意平面由空间一点及两个不共线向量唯一确定.
我们知道,给定空间一点 A 和一条直线 l,则过点 A 且垂直于直线 l 的平面是唯一确定的.
B
P
p
O
A
C
a
b
1.空间中点、直线和平面的向量表示
二、知识讲解
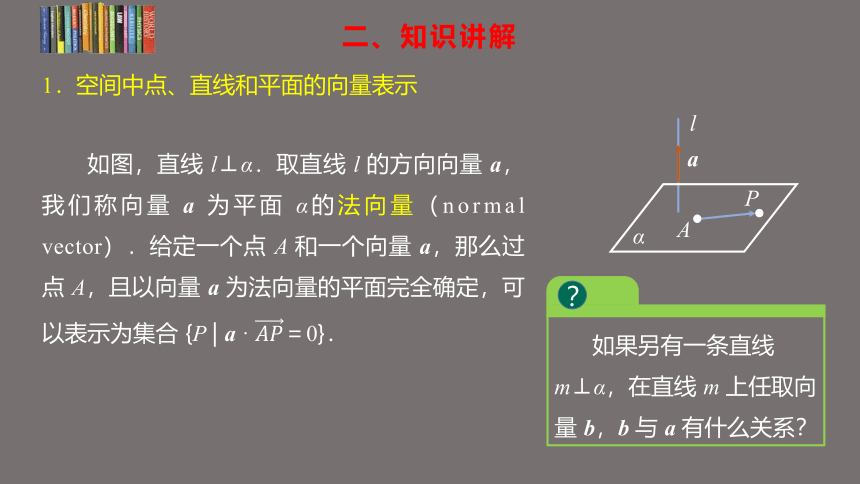
如图,直线 l⊥α.取直线 l 的方向向量 a,我们称向量 a 为平面 α的法向量(normal vector).给定一个点 A 和一个向量 a,那么过点 A,且以向量 a 为法向量的平面完全确定,可以表示为集合 {P | a · =0}.
P
l
A
a
α
如果另有一条直线m⊥α,在直线 m 上任取向量 b,b 与 a 有什么关系?
?
1.空间中点、直线和平面的向量表示
二、知识讲解
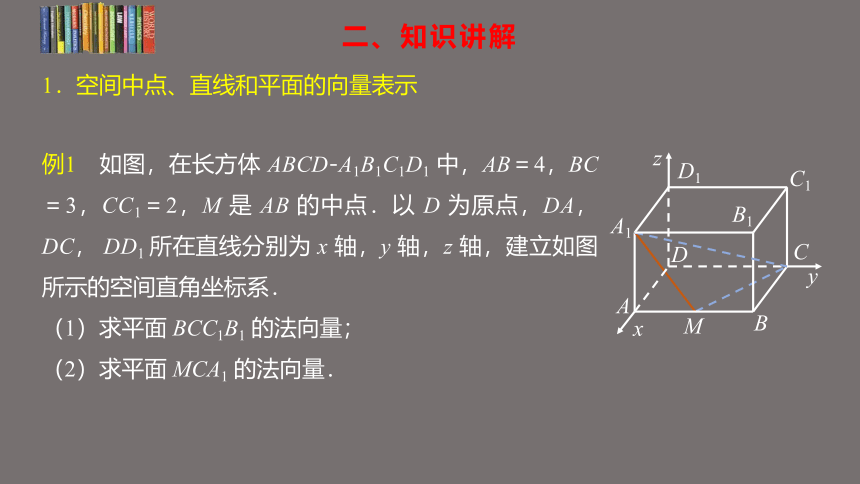
例1 如图,在长方体 ABCD-A1B1C1D1 中,AB=4,BC=3,CC1=2,M 是 AB 的中点.以 D 为原点,DA,DC, DD1 所在直线分别为 x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系.
(1)求平面 BCC1B1 的法向量;
(2)求平面 MCA1 的法向量.
z
x
y
A
A1
B
B1
C
C1
D1
D
M
1.空间中点、直线和平面的向量表示
二、知识讲解
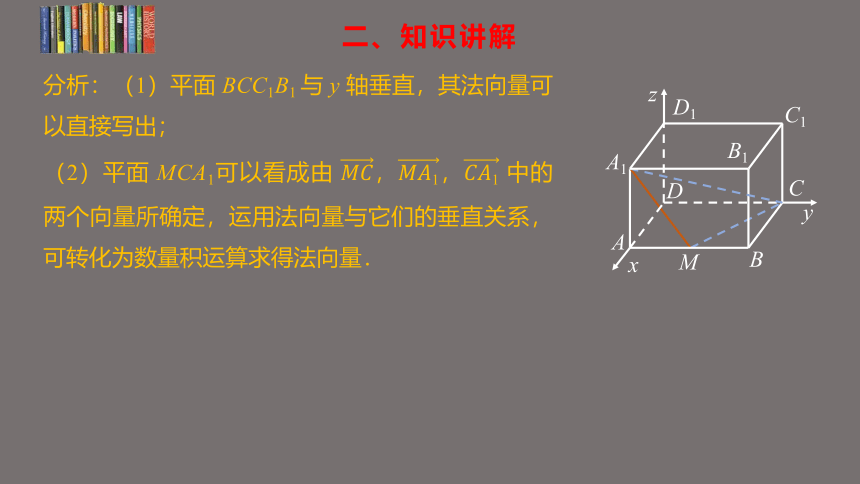
分析:(1)平面 BCC1B1 与 y 轴垂直,其法向量可以直接写出;
(2)平面 MCA1可以看成由 ,, 中的两个向量所确定,运用法向量与它们的垂直关系,可转化为数量积运算求得法向量.
z
x
y
A
A1
B
B1
C
C1
D1
D
M
二、知识讲解
由直线与直线、直线与平面或平面与平面的平行关系,可以得到直线的方向向量、平面的法向量间的什么关系?
?
思考
如图,设 u1,u2 分别是直线 l1,l2 的方向向量.由方向向量的定义可知,如果两条直线平行,那么它们的方向向量一定平行;反过来,如果两条直线的方向向量平行,那么这两条直线也平行.所以 l1∥l2u1∥u2λ∈R,使得 u1 =λu2.
l1
u2
l2
u1
2.空间中直线、平面的平行
二、知识讲解
类似地,如图,设 u 是直线 l 的方向向量,n 是平面 α的法向量,lα则 l∥αu⊥nu ·n=0.
如图,设 n1,n2 分别是平面 α,β的法向量,则α∥βn1∥n2λ∈R,使得 n1 =λn2.
n2
α
β
n1
l
n
u
α
2.空间中直线、平面的平行
二、知识讲解
例2 证明“平面与平面平行的判定定理”:若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
已知:如图 αβ,bβ,a∩b=P,a∥α, b∥α.
求证:α∥β.
分析:设平面 α的法向量为 n,直线 a,b 的方向向量分别为 u,v,则由已知条件可得 n · u=n · v=0,由此可以证明 n 与平面 β内的任意一个向量垂直,即 n 也是 β的法向量.
α
β
n
P
v
u
a
b
2.空间中直线、平面的平行
二、知识讲解
例3 如图,在长方体 ABCD-A1B1C1D1中,AB=4,BC=3,CC1=2,线段 B1C 上是否存在点 P,使得 A1P∥平面 ACD1?
分析:根据条件建立适当的空间直角坐标系,那么问题中涉及的点、向量 ,,以及平面 ACD1 的法向量n 等都可以用坐标表示.如果点 P 存在,那么就有 n ·=0,由此通过向量的坐标运算可得结果.
z
x
y
A
A1
B
B1
C
C1
D1
D
P
2.空间中直线、平面的平行
二、知识讲解
类似空间中直线、平面平行的向量表示,在直线与直线、直线与平面、平面与平面的垂直关系中,直线的方向向量、平面的法向量之间有什么关系?
?
思考
一般地,直线与直线垂直,就是两直线的方向向量垂直;直线与平面垂直,就是直线的方向向量与平面的法向量平行;平面与平面垂直,就是两平面的法向量垂直.
3.空间中直线、平面的垂直
二、知识讲解
如图,设直线 l1,l2 的方向向量分别为 u1,u2,则l1⊥l2u1⊥u2u1 · u2=0.
如图,设直线 l的方向向量为 u,平面 α的法向量为n,则l⊥αu∥nλ∈R,使得 u=λn.
如图,设平面 α,β的法向量分别为 n1,n2,则α ⊥βn1⊥n2n1 · n2=0.
u1
l1
l2
u2
α
n
l2
u2
α
n1
β
n2
α
3.空间中直线、平面的垂直
二、知识讲解
我们随时随地看到向量运算的作用,你同意“向量是躯体,运算是灵魂” “没有运算的向量只能起路标的作用”的说法吗?
?
3.空间中直线、平面的垂直
二、知识讲解
例4 如图,在平行六面体 ABCD-A1B1C1D1中,AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,求证:直线A1C⊥平面 BDD1B1.
分析:根据条件,可以 {,,} 为基底,并用基向量表示 和平面 BDD1B1,再通过向量运算证明 是平面 BDD1B1 的法向量即可.
A
A1
B
B1
C
C1
D1
D
3.空间中直线、平面的垂直
二、知识讲解
例5 证明“平面与平面垂直的判定定理”:若一个平面过另一个平面的垂线,则这两个平面垂直.
已知:如图,l⊥α,lβ,求证:α⊥β.
证明:取直线 l 的方向向量 u,平面 β的法向量 n.
因为 l⊥α,所以 u 是平面 α的法向量.
因为 lβ,而 n 是平面 β的法向量,所以 u⊥n.
所以 α⊥β.
u
β
n
α
l
3.空间中直线、平面的垂直
二、知识讲解
如图,向量 在直线 l 上的投影向量为 ,则 APQ 是直角三角形.因为 A,P 都是定点,所以 ||, 与 u 的夹角∠PAQ 都是确定的.于是可求 ||.再利用勾股定理,可以求出点 P 到直线 l 的距离 PQ.
P
A
Q
u
l
已知直线 l 的单位方向向量为 u,A 是直线 l 上的定点,P 是直线 l 外一点.如何利用这些条件求点 P 到直线 l 的距离?
探究
4.用空间向量研究距离问题
二、知识讲解
设 =a,则向量 在直线 l 上的投影向量 =(a·u)u.
在 RtAPQ 中,由勾股定理,得
PQ==.
P
A
Q
u
l
类比点到直线的距离的求法,如何求两条平行直线之间的距离?
?
思考
4.用空间向量研究距离问题
二、知识讲解
我们再来看平面 α外一点 P 到平面 α的距离问题.
如图,已知平面 α的法向量为 n,A 是平面 α内的定点,P 是平面 α外一点.过点 P 作平面 α的垂线 l,交平面 α于点 Q,则 n 是直线 l 的方向向量,且点 P 到平面 α的距离就是 在直线 l 上的投影向量 的长度.因此
PQ===.
P
A
Q
n
l
α
4.用空间向量研究距离问题
二、知识讲解
例6 如图,在棱长为 1 的正方体 ABCD-A1B1C1D1 中,E 为线段 A1B1 的中点,F 为线段 AB 的中点.
(1)求点 B 到直线 AC1 的距离;
(2)求直线 FC 到平面 AEC1 的距离.
分析:根据条件建立空间直角坐标系,用坐标表示相关的点、直线的方向向量和平面的法向量,再利用有关公式,通过坐标运算得出相应的距离.
z
x
y
A
A1
B
B1
C
C1
D1
E
D
F
4.用空间向量研究距离问题
二、知识讲解
与用平面向量解决平面几何问题的“三步曲”类似,我们可以得出用空间向量解决立体几何问题的“三步曲”:
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹角等问题;
(3)把向量运算的结果“翻译”成相应的几何结论.
4.用空间向量研究距离问题
二、知识讲解
例7 如图,在棱长为 1 的正四面体(四个面都是正三角形)ABCD中,M,N 分别为 BC,AD 的中点,求直线 AM 和 CN 夹角的余弦值.
分析:求直线 AM 和 CN 夹角的余弦值,可以转化为求向量 与 夹角的余弦值.为此需要把向量 , 用适当的基底表示出来,进而求得向量 , 夹角的余弦值.
A
B
C
M
D
N
5.用空间向量研究夹角问题
二、知识讲解
以上我们用向量方法解决了异面直线 AM 和 CN 所成角的问题,你能用向量方法求直线 AB 与平面 BCD 所成的角吗?
?
思考
一般地,两条异面直线所成的角,可以转化为两条异面直线的方向向量的夹角来求得.也就是说,若异面直线l1,l2 所成的角为 θ,其方向向量分别是 u,v,则cosθ=|cos|==.
5.用空间向量研究夹角问题
二、知识讲解
类似地,直线与平面所成的角,可以转化为直线的方向向量与平面的法向量的夹角.如图,直线 AB与平面 α相交于点 B,设直线 AB 与平面 α所成的角为 θ,直线 AB 的方向向量 u,平面 α的法向量为 n,则
sinθ=|cos|==.
θ
A
C
n
B
α
u
5.用空间向量研究夹角问题
二、知识讲解
如图,平面 α与平面 β相交,形成四个二面角,我们把这四个二面角中不大于 90° 的二面角称为平面 α与平面 β的夹角.
类似于两条异面直线所成的角,若平面 α,β的法向量分别是 n1 和 n2,则平面 α与平面 β的夹角即为向量 n1 和 n2 的夹角或其补角.设平面 α与平面 β的夹角为 θ,则cosθ=|cos|==.
β
α
n1
n2
图中有几个二面角?两个平面的夹角与这两个平面形成的二面角有什么关系?
?
5.用空间向量研究夹角问题
二、知识讲解
例8 如图,在直三棱柱 ABC-A1B1C1 中,AC=CB=2, AA1=3,∠ACB=90°,P 为线段 BC 的中点,点 Q,R 分别在棱 AA1,BB1 上,A1Q=2AQ,BR=2RB1.求平面PQR 与平面 A1B1C1 夹角的余弦值.
分析:因为平面 PQR 与平面 A1B1C1 的夹角可以转化为平面 PQR 与 A1B1C1 的法向量的夹角,所以只需要求出这两个平面的法向量的夹角即可.
z
x
y
A
A1
B
B1
C
C1
Q
R
P
5.用空间向量研究夹角问题
二、知识讲解
例9 图为某种礼物降落伞的示意图,其中有 8 根绳子和伞面连接,每根绳子和水平面的法向量的夹角均为 30°.已知礼物的质量为 1 kg,每根绳子的拉力大小相同.求降落伞在匀速下落的过程中每根绳子拉力的大小(重力加速度 g 取 9.8 m/s2,精确到 0.01 N).
分析:因为降落伞匀速下落,所以降落伞 8 根绳子拉力的合力的大小等于礼物重力的大小.8 根绳子的拉力在水平面的法向量方向上的投影向量的和向量与礼物的重力是一对相反向量.
F
|F|n
n
6.空间向量的综合应用
二、知识讲解
例10 如图,在四棱锥 P-ABCD 中,底面 ABCD 是正方形,侧棱 PD⊥底面 ABCD,PD=DC,E 是 PC 的中点,作 EF⊥PB 交 PB 于点 F.
(1)求证:PA∥平面 EDB;
(2)求证:PB⊥平面 EFD;
(3)求平面 CPB 与平面 PBD 的夹角的大小.
A
B
C
D
E
P
F
6.空间向量的综合应用
二、知识讲解
分析:本题涉及的问题包括:直线与平面平行和垂直的判定,计算两个平面的夹角.这些问题都可以利用向量方法解决.由于四棱锥的底面是正方形,而且一条侧棱垂直于底面,可以利用这些条件建立适当的空间直角坐标系,用向量及坐标表示问题中的几何元素,进而解决问题.
z
x
y
G
A
B
C
D
E
P
F
6.空间向量的综合应用
二、知识讲解
通过本节的学习,你对立体几何中的向量法是否有了一定的认识?请结合例题就下面的框图谈谈体会.
用空间向量表示立体图形中点、直线、平面等元素
进行空间向量的运算,研究点、直线、平面之间的关系
把运算结果“翻译”成相应的几何意义
解决立体几何中的问题,可用三种方法:综合法、向量法、坐标法.你能说出它们各自的特点吗?
三、小结
空间向量的应用
证明平行
证明垂直
求距离
求空间角
直线与平面所成角
异面直线所成角
平面与平面的夹角
点到直线的距离
点到平面的距离
线面垂直
线线垂直
面面垂直
线面平行
线线平行
面面平行
1.判断下列命题是否正确,正确的在括号内打“√”,错误的打“×”.
(1)零向量不能作为直线的方向向量和平面的法向量;( )
(2)若 v 是直线 l 的方向向量,则 λv(λ∈R) 也是直线 l 的方向向量;( )
(3)在空间直角坐标系中,j=(0,0,1) 是坐标平面 Oxy 的一个法向量.( )
答案:(1)√;(2)×;(3)√.
四、练习
2.用向量方法证明“直线与平面平行的判定定理”:若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
答案:已知:直线 l,m 和平面 α,其中 lα,mα,l∥m,求证:l∥α,
证明:设直线 l,m 的方向向量分别为 a,b,平面 α的法向量为 u,因为 l∥m,所以 a=kb,k∈R,因为平面 α的法向量为 u,所以 u⊥α,因为 mα,直线 m 的方向向量为 b,所以 u⊥b,所以 u · b=0,所以 u· a=u· (kb)=ku· b=0,所以 u⊥a,因为 lα,所以 l∥α.
四、练习
3.已知 u=(3,a+b,a-b)(a,b∈R)是直线 l 的方向向量,n=(1,2,3)是平面 α的法向量.
(1)若 l∥α,求 a,b 的关系式;(2)若 l⊥α,求 a,b 的值.
答案:(1)5a-b+3=0;(2)a=,b=-.
4.在棱长为 1 的正方体 ABCD-A1B1C1D1中,点 A 到平面 B1C 的距离等于______;直线 DC 到平面 AB1 的距离等于_____;平面 DA1 到平面 CB1 的距离等于______.
答案:1;1;1.
四、练习
5.在直三棱柱 ABC-A1B1C1中,∠BCA=90°,D1,F1分别是 A1B1,A1C1 的中点,BC=CA=CC1,则 BD1 与 AF1 所成角的余弦值是( ).
(A) (B) (C) (D)
答案:A.
四、练习
五、本章知识结构
空间向量的概念及其应用
空间向量的定义及表示
空间向量的线性运算和数量积运算
空间向量运算的运算律
空间向量运算的定义及其几何意义
用空间向量研究立体几何中的直线、平面的位置关系、距离和夹角问题
用空间向量表示点、直线、平面等元素
把向量运算的结果“翻译”成相应的几何结论
空间直角坐标系
空间向量运算的坐标表示
用空间向量解决立体几何问题
空间向量基本定理与空间向量运算的坐标表示
空间向量基本定理
1.4 空间向量的应用
第一章 空间向量与立体几何
目录
二、知识讲解
三、小结
四、练习
一、上节回溯
五、本章知识结构
一、上节回溯
空间向量及其
运算的坐标表示
空间直角
坐标系
空间中点的坐标表示
空间两点间的距离表示
空间向量的坐标表示
空间向量运算的坐标表示
数乘运算
加减运算
数量积运算
1.空间中点、直线和平面的向量表示
二、知识讲解
如何用向量表示空间中的一个点?
?
思考
如图,在空间中,我们取一定点 O 作为基点,那么空间中任意一点 P 就可以用向量 来表示.我们把向量 称为点 P 的位置向量.
P
p
O
二、知识讲解
我们知道,空间中给定一个点 A 和一个方向就能唯一确定一条直线 l.如何用向量表示直线 l ?
?
思考
如图,a是直线 l 的方向向量,在直线 l 上取 =a,设 P是直线 l 上的任意一点,由向量共线的条件可知,点 P 在直线 l 上的充要条件是存在实数 t,使得
=ta,即 =t.
a
A
P
B
l
1.空间中点、直线和平面的向量表示
二、知识讲解
你能证明这个结论吗?
?
进一步地,如图,取定空间中的任意一点 O,可以得到点 P 在直线 l 上的充要条件是存在实数 t,使
=+ta, ①
将 =a 代入 ①式,得
=+t. ②
① 式和 ②式都称为空间直线的向量表示式.由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.
a
A
P
B
l
O
1.空间中点、直线和平面的向量表示
二、知识讲解
一个定点和两个定方向能否确定一个平面?进一步地,一个定点和一个定方向能否确定一个平面?如果能确定,如何用向量表示这个平面?
?
思考
我们知道,平面 α可以由 α内两条相交直线确定.如图,设两条直线相交于点 O,它们的方向向量分别为 a和 b,P为平面 α内任意一点,由平面向量基本定理可知,存在唯一的有序实数对 (x,y),使得 =xa+yb .
P
b
O
a
α
1.空间中点、直线和平面的向量表示
二、知识讲解
进一步地,如图,取定空间任意一点 O,可以得到,空间一点 P 位于平面 ABC 内的充要条件是存在实数 x,y,使
=+x+y.③
我们把 ③式称为空间平面 ABC 的向量表示式.由此可知,空间中任意平面由空间一点及两个不共线向量唯一确定.
我们知道,给定空间一点 A 和一条直线 l,则过点 A 且垂直于直线 l 的平面是唯一确定的.
B
P
p
O
A
C
a
b
1.空间中点、直线和平面的向量表示
二、知识讲解
如图,直线 l⊥α.取直线 l 的方向向量 a,我们称向量 a 为平面 α的法向量(normal vector).给定一个点 A 和一个向量 a,那么过点 A,且以向量 a 为法向量的平面完全确定,可以表示为集合 {P | a · =0}.
P
l
A
a
α
如果另有一条直线m⊥α,在直线 m 上任取向量 b,b 与 a 有什么关系?
?
1.空间中点、直线和平面的向量表示
二、知识讲解
例1 如图,在长方体 ABCD-A1B1C1D1 中,AB=4,BC=3,CC1=2,M 是 AB 的中点.以 D 为原点,DA,DC, DD1 所在直线分别为 x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系.
(1)求平面 BCC1B1 的法向量;
(2)求平面 MCA1 的法向量.
z
x
y
A
A1
B
B1
C
C1
D1
D
M
1.空间中点、直线和平面的向量表示
二、知识讲解
分析:(1)平面 BCC1B1 与 y 轴垂直,其法向量可以直接写出;
(2)平面 MCA1可以看成由 ,, 中的两个向量所确定,运用法向量与它们的垂直关系,可转化为数量积运算求得法向量.
z
x
y
A
A1
B
B1
C
C1
D1
D
M
二、知识讲解
由直线与直线、直线与平面或平面与平面的平行关系,可以得到直线的方向向量、平面的法向量间的什么关系?
?
思考
如图,设 u1,u2 分别是直线 l1,l2 的方向向量.由方向向量的定义可知,如果两条直线平行,那么它们的方向向量一定平行;反过来,如果两条直线的方向向量平行,那么这两条直线也平行.所以 l1∥l2u1∥u2λ∈R,使得 u1 =λu2.
l1
u2
l2
u1
2.空间中直线、平面的平行
二、知识讲解
类似地,如图,设 u 是直线 l 的方向向量,n 是平面 α的法向量,lα则 l∥αu⊥nu ·n=0.
如图,设 n1,n2 分别是平面 α,β的法向量,则α∥βn1∥n2λ∈R,使得 n1 =λn2.
n2
α
β
n1
l
n
u
α
2.空间中直线、平面的平行
二、知识讲解
例2 证明“平面与平面平行的判定定理”:若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
已知:如图 αβ,bβ,a∩b=P,a∥α, b∥α.
求证:α∥β.
分析:设平面 α的法向量为 n,直线 a,b 的方向向量分别为 u,v,则由已知条件可得 n · u=n · v=0,由此可以证明 n 与平面 β内的任意一个向量垂直,即 n 也是 β的法向量.
α
β
n
P
v
u
a
b
2.空间中直线、平面的平行
二、知识讲解
例3 如图,在长方体 ABCD-A1B1C1D1中,AB=4,BC=3,CC1=2,线段 B1C 上是否存在点 P,使得 A1P∥平面 ACD1?
分析:根据条件建立适当的空间直角坐标系,那么问题中涉及的点、向量 ,,以及平面 ACD1 的法向量n 等都可以用坐标表示.如果点 P 存在,那么就有 n ·=0,由此通过向量的坐标运算可得结果.
z
x
y
A
A1
B
B1
C
C1
D1
D
P
2.空间中直线、平面的平行
二、知识讲解
类似空间中直线、平面平行的向量表示,在直线与直线、直线与平面、平面与平面的垂直关系中,直线的方向向量、平面的法向量之间有什么关系?
?
思考
一般地,直线与直线垂直,就是两直线的方向向量垂直;直线与平面垂直,就是直线的方向向量与平面的法向量平行;平面与平面垂直,就是两平面的法向量垂直.
3.空间中直线、平面的垂直
二、知识讲解
如图,设直线 l1,l2 的方向向量分别为 u1,u2,则l1⊥l2u1⊥u2u1 · u2=0.
如图,设直线 l的方向向量为 u,平面 α的法向量为n,则l⊥αu∥nλ∈R,使得 u=λn.
如图,设平面 α,β的法向量分别为 n1,n2,则α ⊥βn1⊥n2n1 · n2=0.
u1
l1
l2
u2
α
n
l2
u2
α
n1
β
n2
α
3.空间中直线、平面的垂直
二、知识讲解
我们随时随地看到向量运算的作用,你同意“向量是躯体,运算是灵魂” “没有运算的向量只能起路标的作用”的说法吗?
?
3.空间中直线、平面的垂直
二、知识讲解
例4 如图,在平行六面体 ABCD-A1B1C1D1中,AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,求证:直线A1C⊥平面 BDD1B1.
分析:根据条件,可以 {,,} 为基底,并用基向量表示 和平面 BDD1B1,再通过向量运算证明 是平面 BDD1B1 的法向量即可.
A
A1
B
B1
C
C1
D1
D
3.空间中直线、平面的垂直
二、知识讲解
例5 证明“平面与平面垂直的判定定理”:若一个平面过另一个平面的垂线,则这两个平面垂直.
已知:如图,l⊥α,lβ,求证:α⊥β.
证明:取直线 l 的方向向量 u,平面 β的法向量 n.
因为 l⊥α,所以 u 是平面 α的法向量.
因为 lβ,而 n 是平面 β的法向量,所以 u⊥n.
所以 α⊥β.
u
β
n
α
l
3.空间中直线、平面的垂直
二、知识讲解
如图,向量 在直线 l 上的投影向量为 ,则 APQ 是直角三角形.因为 A,P 都是定点,所以 ||, 与 u 的夹角∠PAQ 都是确定的.于是可求 ||.再利用勾股定理,可以求出点 P 到直线 l 的距离 PQ.
P
A
Q
u
l
已知直线 l 的单位方向向量为 u,A 是直线 l 上的定点,P 是直线 l 外一点.如何利用这些条件求点 P 到直线 l 的距离?
探究
4.用空间向量研究距离问题
二、知识讲解
设 =a,则向量 在直线 l 上的投影向量 =(a·u)u.
在 RtAPQ 中,由勾股定理,得
PQ==.
P
A
Q
u
l
类比点到直线的距离的求法,如何求两条平行直线之间的距离?
?
思考
4.用空间向量研究距离问题
二、知识讲解
我们再来看平面 α外一点 P 到平面 α的距离问题.
如图,已知平面 α的法向量为 n,A 是平面 α内的定点,P 是平面 α外一点.过点 P 作平面 α的垂线 l,交平面 α于点 Q,则 n 是直线 l 的方向向量,且点 P 到平面 α的距离就是 在直线 l 上的投影向量 的长度.因此
PQ===.
P
A
Q
n
l
α
4.用空间向量研究距离问题
二、知识讲解
例6 如图,在棱长为 1 的正方体 ABCD-A1B1C1D1 中,E 为线段 A1B1 的中点,F 为线段 AB 的中点.
(1)求点 B 到直线 AC1 的距离;
(2)求直线 FC 到平面 AEC1 的距离.
分析:根据条件建立空间直角坐标系,用坐标表示相关的点、直线的方向向量和平面的法向量,再利用有关公式,通过坐标运算得出相应的距离.
z
x
y
A
A1
B
B1
C
C1
D1
E
D
F
4.用空间向量研究距离问题
二、知识讲解
与用平面向量解决平面几何问题的“三步曲”类似,我们可以得出用空间向量解决立体几何问题的“三步曲”:
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹角等问题;
(3)把向量运算的结果“翻译”成相应的几何结论.
4.用空间向量研究距离问题
二、知识讲解
例7 如图,在棱长为 1 的正四面体(四个面都是正三角形)ABCD中,M,N 分别为 BC,AD 的中点,求直线 AM 和 CN 夹角的余弦值.
分析:求直线 AM 和 CN 夹角的余弦值,可以转化为求向量 与 夹角的余弦值.为此需要把向量 , 用适当的基底表示出来,进而求得向量 , 夹角的余弦值.
A
B
C
M
D
N
5.用空间向量研究夹角问题
二、知识讲解
以上我们用向量方法解决了异面直线 AM 和 CN 所成角的问题,你能用向量方法求直线 AB 与平面 BCD 所成的角吗?
?
思考
一般地,两条异面直线所成的角,可以转化为两条异面直线的方向向量的夹角来求得.也就是说,若异面直线l1,l2 所成的角为 θ,其方向向量分别是 u,v,则cosθ=|cos
5.用空间向量研究夹角问题
二、知识讲解
类似地,直线与平面所成的角,可以转化为直线的方向向量与平面的法向量的夹角.如图,直线 AB与平面 α相交于点 B,设直线 AB 与平面 α所成的角为 θ,直线 AB 的方向向量 u,平面 α的法向量为 n,则
sinθ=|cos
θ
A
C
n
B
α
u
5.用空间向量研究夹角问题
二、知识讲解
如图,平面 α与平面 β相交,形成四个二面角,我们把这四个二面角中不大于 90° 的二面角称为平面 α与平面 β的夹角.
类似于两条异面直线所成的角,若平面 α,β的法向量分别是 n1 和 n2,则平面 α与平面 β的夹角即为向量 n1 和 n2 的夹角或其补角.设平面 α与平面 β的夹角为 θ,则cosθ=|cos
β
α
n1
n2
图中有几个二面角?两个平面的夹角与这两个平面形成的二面角有什么关系?
?
5.用空间向量研究夹角问题
二、知识讲解
例8 如图,在直三棱柱 ABC-A1B1C1 中,AC=CB=2, AA1=3,∠ACB=90°,P 为线段 BC 的中点,点 Q,R 分别在棱 AA1,BB1 上,A1Q=2AQ,BR=2RB1.求平面PQR 与平面 A1B1C1 夹角的余弦值.
分析:因为平面 PQR 与平面 A1B1C1 的夹角可以转化为平面 PQR 与 A1B1C1 的法向量的夹角,所以只需要求出这两个平面的法向量的夹角即可.
z
x
y
A
A1
B
B1
C
C1
Q
R
P
5.用空间向量研究夹角问题
二、知识讲解
例9 图为某种礼物降落伞的示意图,其中有 8 根绳子和伞面连接,每根绳子和水平面的法向量的夹角均为 30°.已知礼物的质量为 1 kg,每根绳子的拉力大小相同.求降落伞在匀速下落的过程中每根绳子拉力的大小(重力加速度 g 取 9.8 m/s2,精确到 0.01 N).
分析:因为降落伞匀速下落,所以降落伞 8 根绳子拉力的合力的大小等于礼物重力的大小.8 根绳子的拉力在水平面的法向量方向上的投影向量的和向量与礼物的重力是一对相反向量.
F
|F|n
n
6.空间向量的综合应用
二、知识讲解
例10 如图,在四棱锥 P-ABCD 中,底面 ABCD 是正方形,侧棱 PD⊥底面 ABCD,PD=DC,E 是 PC 的中点,作 EF⊥PB 交 PB 于点 F.
(1)求证:PA∥平面 EDB;
(2)求证:PB⊥平面 EFD;
(3)求平面 CPB 与平面 PBD 的夹角的大小.
A
B
C
D
E
P
F
6.空间向量的综合应用
二、知识讲解
分析:本题涉及的问题包括:直线与平面平行和垂直的判定,计算两个平面的夹角.这些问题都可以利用向量方法解决.由于四棱锥的底面是正方形,而且一条侧棱垂直于底面,可以利用这些条件建立适当的空间直角坐标系,用向量及坐标表示问题中的几何元素,进而解决问题.
z
x
y
G
A
B
C
D
E
P
F
6.空间向量的综合应用
二、知识讲解
通过本节的学习,你对立体几何中的向量法是否有了一定的认识?请结合例题就下面的框图谈谈体会.
用空间向量表示立体图形中点、直线、平面等元素
进行空间向量的运算,研究点、直线、平面之间的关系
把运算结果“翻译”成相应的几何意义
解决立体几何中的问题,可用三种方法:综合法、向量法、坐标法.你能说出它们各自的特点吗?
三、小结
空间向量的应用
证明平行
证明垂直
求距离
求空间角
直线与平面所成角
异面直线所成角
平面与平面的夹角
点到直线的距离
点到平面的距离
线面垂直
线线垂直
面面垂直
线面平行
线线平行
面面平行
1.判断下列命题是否正确,正确的在括号内打“√”,错误的打“×”.
(1)零向量不能作为直线的方向向量和平面的法向量;( )
(2)若 v 是直线 l 的方向向量,则 λv(λ∈R) 也是直线 l 的方向向量;( )
(3)在空间直角坐标系中,j=(0,0,1) 是坐标平面 Oxy 的一个法向量.( )
答案:(1)√;(2)×;(3)√.
四、练习
2.用向量方法证明“直线与平面平行的判定定理”:若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
答案:已知:直线 l,m 和平面 α,其中 lα,mα,l∥m,求证:l∥α,
证明:设直线 l,m 的方向向量分别为 a,b,平面 α的法向量为 u,因为 l∥m,所以 a=kb,k∈R,因为平面 α的法向量为 u,所以 u⊥α,因为 mα,直线 m 的方向向量为 b,所以 u⊥b,所以 u · b=0,所以 u· a=u· (kb)=ku· b=0,所以 u⊥a,因为 lα,所以 l∥α.
四、练习
3.已知 u=(3,a+b,a-b)(a,b∈R)是直线 l 的方向向量,n=(1,2,3)是平面 α的法向量.
(1)若 l∥α,求 a,b 的关系式;(2)若 l⊥α,求 a,b 的值.
答案:(1)5a-b+3=0;(2)a=,b=-.
4.在棱长为 1 的正方体 ABCD-A1B1C1D1中,点 A 到平面 B1C 的距离等于______;直线 DC 到平面 AB1 的距离等于_____;平面 DA1 到平面 CB1 的距离等于______.
答案:1;1;1.
四、练习
5.在直三棱柱 ABC-A1B1C1中,∠BCA=90°,D1,F1分别是 A1B1,A1C1 的中点,BC=CA=CC1,则 BD1 与 AF1 所成角的余弦值是( ).
(A) (B) (C) (D)
答案:A.
四、练习
五、本章知识结构
空间向量的概念及其应用
空间向量的定义及表示
空间向量的线性运算和数量积运算
空间向量运算的运算律
空间向量运算的定义及其几何意义
用空间向量研究立体几何中的直线、平面的位置关系、距离和夹角问题
用空间向量表示点、直线、平面等元素
把向量运算的结果“翻译”成相应的几何结论
空间直角坐标系
空间向量运算的坐标表示
用空间向量解决立体几何问题
空间向量基本定理与空间向量运算的坐标表示
空间向量基本定理
