粤沪版物理九年级上册课课练:14.3 欧姆定律的应用 第2课时 欧姆定律在串、并联电路中的应用(含答案)
文档属性
| 名称 | 粤沪版物理九年级上册课课练:14.3 欧姆定律的应用 第2课时 欧姆定律在串、并联电路中的应用(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 232.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪粤版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-25 14:23:14 | ||
图片预览

文档简介
[14.3 欧姆定律的应用 第2课时 欧姆定律在串、并联电路中的应用]
一、选择题
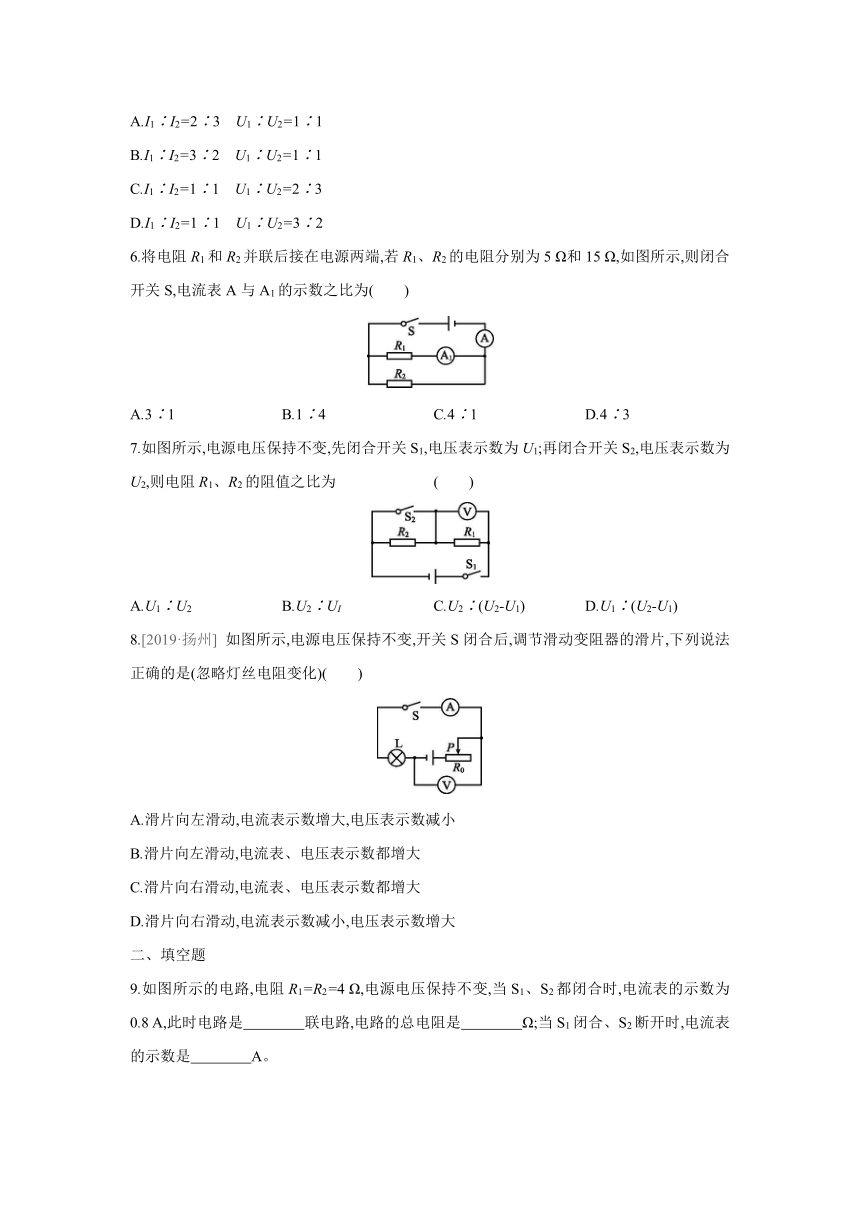
1.已知电阻阻值R1>R2,中阻值最大的是 ( )
2.如图所示,电源电压恒定,闭合开关S后,向右移动R2的滑片时,电路的总电阻将 ( )
A.变大 B.变小
C.不变 D.三种情况均有可能
3.有两个可变电阻,开始时阻值相等,都为R,现将其中一个电阻的阻值增大,将另一个电阻的阻值减小,则两个电阻并联后总电阻将 ( )
A.一定大于R B.一定等于R
C.一定小于R D.以上结果都有可能
4.有两个电阻以一定的方式连接在电压为6 V的电源上,若测得电流为0.5 A,则这两个电阻的阻值及连接方式是 ( )
A.R1=8 Ω R2=4 Ω 并联
B.R1=10 Ω R2=2 Ω 并联
C.R1=20 Ω R2=30 Ω 串联
D.R1=20 Ω R2=30 Ω 并联
5.如图所示,灯泡L1、L2的电阻分别为20 Ω和30 Ω。闭合开关S,通过灯泡L1、L2的电流分别为I1、I2,它们两端的电压分别为U1、U2,则下列选项正确的是 ( )
A.I1∶I2=2∶3 U1∶U2=1∶1
B.I1∶I2=3∶2 U1∶U2=1∶1
C.I1∶I2=1∶1 U1∶U2=2∶3
D.I1∶I2=1∶1 U1∶U2=3∶2
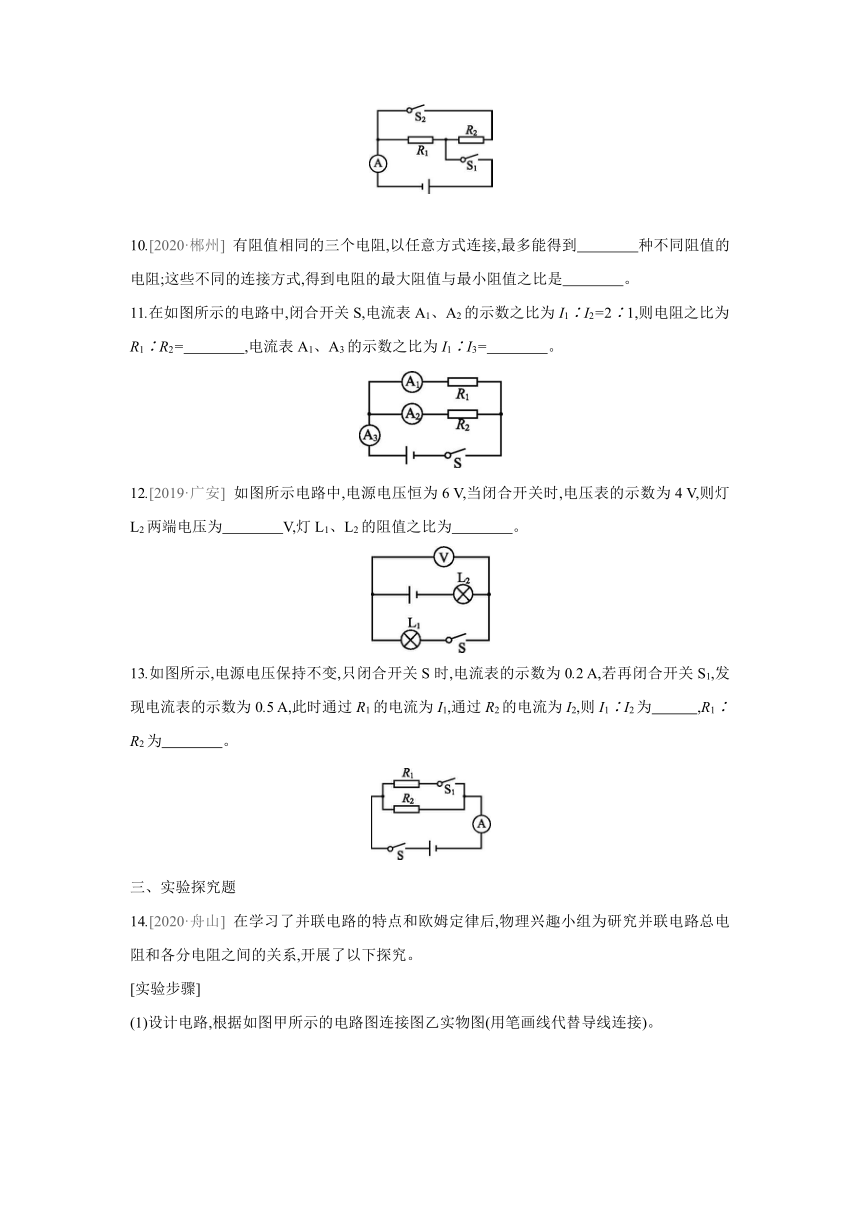
6.将电阻R1和R2并联后接在电源两端,若R1、R2的电阻分别为5 Ω和15 Ω,如图所示,则闭合开关S,电流表A与A1的示数之比为( )
A.3∶1 B.1∶4 C.4∶1 D.4∶3
7.如图所示,电源电压保持不变,先闭合开关S1,电压表示数为U1;再闭合开关S2,电压表示数为U2,则电阻R1、R2的阻值之比为 ( )
A.U1∶U2 B.U2∶UI C.U2∶(U2-U1) D.U1∶(U2-U1)
8.[2019·扬州] 如图所示,电源电压保持不变,开关S闭合后,调节滑动变阻器的滑片,下列说法正确的是(忽略灯丝电阻变化)( )
A.滑片向左滑动,电流表示数增大,电压表示数减小
B.滑片向左滑动,电流表、电压表示数都增大
C.滑片向右滑动,电流表、电压表示数都增大
D.滑片向右滑动,电流表示数减小,电压表示数增大
二、填空题
9.如图所示的电路,电阻R1=R2=4 Ω,电源电压保持不变,当S1、S2都闭合时,电流表的示数为0.8 A,此时电路是 联电路,电路的总电阻是 Ω;当S1闭合、S2断开时,电流表的示数是 A。
10.[2020·郴州] 有阻值相同的三个电阻,以任意方式连接,最多能得到 种不同阻值的电阻;这些不同的连接方式,得到电阻的最大阻值与最小阻值之比是 。
11.在如图所示的电路中,闭合开关S,电流表A1、A2的示数之比为I1∶I2=2∶1,则电阻之比为R1∶R2= ,电流表A1、A3的示数之比为I1∶I3= 。
12.[2019·广安] 如图所示电路中,电源电压恒为6 V,当闭合开关时,电压表的示数为4 V,则灯L2两端电压为 V,灯L1、L2的阻值之比为 。
13.如图所示,电源电压保持不变,只闭合开关S时,电流表的示数为0.2 A,若再闭合开关S1,发现电流表的示数为0.5 A,此时通过R1的电流为I1,通过R2的电流为I2,则I1∶I2为 ,R1∶R2为 。
三、实验探究题
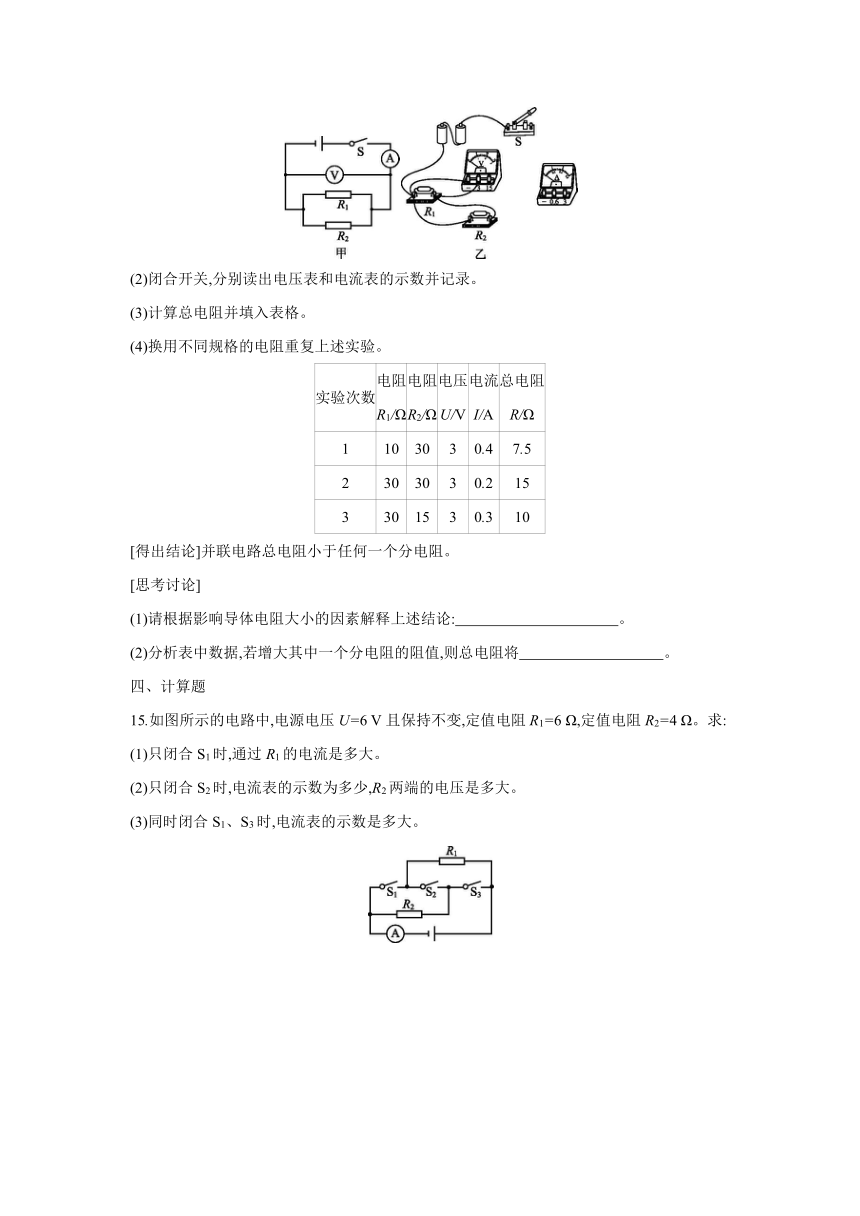
14.[2020·舟山] 在学习了并联电路的特点和欧姆定律后,物理兴趣小组为研究并联电路总电阻和各分电阻之间的关系,开展了以下探究。
[实验步骤]
(1)设计电路,根据如图甲所示的电路图连接图乙实物图(用笔画线代替导线连接)。
(2)闭合开关,分别读出电压表和电流表的示数并记录。
(3)计算总电阻并填入表格。
(4)换用不同规格的电阻重复上述实验。
实验次数 电阻 R1/Ω 电阻 R2/Ω 电压 U/V 电流 I/A 总电阻 R/Ω
1 10 30 3 0.4 7.5
2 30 30 3 0.2 15
3 30 15 3 0.3 10
[得出结论]并联电路总电阻小于任何一个分电阻。
[思考讨论]
(1)请根据影响导体电阻大小的因素解释上述结论: 。
(2)分析表中数据,若增大其中一个分电阻的阻值,则总电阻将 。
四、计算题
15.如图所示的电路中,电源电压U=6 V且保持不变,定值电阻R1=6 Ω,定值电阻R2=4 Ω。求:
(1)只闭合S1时,通过R1的电流是多大。
(2)只闭合S2时,电流表的示数为多少,R2两端的电压是多大。
(3)同时闭合S1、S3时,电流表的示数是多大。
16.[2019·自贡] 已知电源电压不变,为了比较电阻R1和R2的大小,同学们分别设计了如图所示的电路,其中不可行的是 ( )
答案
1.B
2.A 由图可知两电阻并联,当滑片右移时,滑动变阻器接入电路的电阻增大,故电路中的总电阻增大。
3.C 因为并联电路总电阻的倒数等于各支路电阻的倒数之和,所以并联电路的总电阻小于任一支路的电阻值,即两个电阻并联后总电阻小于较小电阻的阻值。
4.D
5.B 两灯并联,灯泡L1、L2的电阻分别为20 Ω和30 Ω,由于并联电路各支路两端的电压相等,故L1、L2两端的电压之比U1∶U2=1∶1;根据I=可知,电压相等时,通过灯泡的电流与灯泡的电阻成反比,则通过灯泡L1、L2的电流之比为I1∶I2=R2∶R1=30 Ω∶20 Ω=3∶2。
6.D 由电路图可知两电阻并联,电流表A测干路电流,电流表A1测R1支路的电流。并联电路具有分流作用,电流的分配与电阻成反比关系,电阻之比R1∶R2=5 Ω∶15 Ω=1∶3,则I1∶I2=3∶1,所以I∶I1=4∶3。
7.D 闭合开关S1、S2时,只有电阻R1连入电路,电压表测量电源电压,则电源电压为U2;只闭合开关S1时,定值电阻R1、R2串联,电压表测量R1两端的电压,则R1两端的电压为U1;因串联电路的总电压等于各部分电路两端电压之和,所以R2两端的电压:U'=U2-U1;串联时通过R1、R2的电流相等,根据欧姆定律可得,R1、R2的阻值之比:===。
8.B 由图可知,灯L与滑动变阻器串联,电压表测量灯L两端的电压;滑片向左滑动,R0减小,电路总电阻减小,电流表和电压表示数均增大,A错误,B正确;滑片向右滑动,R0增大,两表示数均减小,C、D均错误。
9.并 2 0.4
当S1、S2都闭合时,两电阻并联在电路中,电路中的总电阻:R===×4 Ω=2 Ω,电源电压:U=IR=0.8 A×2 Ω=1.6 V;当S1闭合、S2断开时,只有R1接入电路,电路中的电流:I'===0.4 A。
10.7 9∶1 (1)已知三个电阻阻值相同,设一个电阻的阻值为R0,其连接方式可以是:
①一个电阻接入电路,电路总电阻为R1=R0;
②两个电阻串联接入电路,电路总电阻为R2=2R0;
③两个电阻并联接入电路,电路总电阻为R3=R0;
④三个电阻串联接入电路,电路总电阻为R4=3R0;
⑤三个电阻并联接入电路,电路总电阻为R5=R0;
⑥两个电阻先串联再与第三个电阻并联接入电路,电路总电阻为R6=R0;
⑦两个电阻先并联再与第三个电阻串联接入电路,电路总电阻为R7=R0。
所以阻值相同的三个电阻,以任意方式连接,最多能得到7种不同阻值的电阻。
(2)由以上分析知,三个电阻串联接入电路,电路总电阻最大,为R4=3R0;
三个电阻并联接入电路,电路总电阻最小,为R5=R0,
所以得到电阻的最大阻值与最小阻值之比是=。
11.1∶2 2∶3 由电路图可知,电阻R1、R2并联,电流表A1测通过电阻R1的电流,电流表A2测通过电阻R2的电流,电流表A3测干路中的电流,根据并联电路的分流规律可得,R1∶R2=I2∶I1=1∶2;因并联电路干路中的电流等于各支路电流之和,所以,电流表A1、A3的示数之比为===。
12.2 2∶1 由图可知两灯泡串联,则U=U1+U2,且=,电压表测L1两端的电压,即U1=4 V,则U2=U-U1=6 V-4 V=2 V,可得===2∶1。
13.3∶2 2∶3
14.[实验步骤](1)如图图所示
[思考讨论](1)并联后相当于增大了导体的横截面积,在导体材料、长度、温度不变时,导体的横截面积越大,导体的电阻越小
(2)增大
15.(1)由电路图可知,只闭合S1时,只有电阻R1接入电路,通过R1的电流:I1===1 A。
(2)由电路图可知,只闭合S2时,两电阻串联,R1、R2串联的总电阻:R=R1+R2=6 Ω+4 Ω=10 Ω,电路中的电流:I===0.6 A,即电流表的示数为0.6 A。
由欧姆定律I=得,R2两端的电压:
U2=IR2=0.6 A×4 Ω=2.4 V。
(3)同时闭合S1、S3时,R1、R2并联,电流表测干路中的电流,则通过R1的电流:I1'===1 A。通过R2的电流:I2'===1.5 A,则干路电流:I'=I1'+I2'=1 A+1.5 A=2.5 A,即电流表的示数为2.5 A。
16.A 图A中两电阻并联,电压表测电源电压,电流表测量干路电流,只能测出电路的总电阻,不能比较通过电阻R2、R1的电流大小,因此无法比较两电阻阻值的大小,故A符合题意;图B中两电阻串联,两个电压表分别测量两个电阻两端的电压,由于通过两电阻的电流相等,根据电压的大小就可以比较出电阻的大小,故B不符合题意;图C中开关闭合时电路为R1的简单电路,开关断开时两电阻串联,电流表测电路中的电流,根据串联电路的特点和欧姆定律分别表示出电源电压,利用电源电压不变建立等式,通过比较电流之间的关系得出电阻的大小关系,故C不符合题意;图D中两个电阻串联,电压表V1测量串联电阻的总电压,电压表V2测量电阻R1两端的电压,根据串联电路电压的规律,电阻R2两端的电压等于电压表V1和V2的示数之差,这样就可以得到两个电阻两端的电压,根据电压的大小就可以比较电阻的大小,故D不符合题意。
一、选择题
1.已知电阻阻值R1>R2,中阻值最大的是 ( )
2.如图所示,电源电压恒定,闭合开关S后,向右移动R2的滑片时,电路的总电阻将 ( )
A.变大 B.变小
C.不变 D.三种情况均有可能
3.有两个可变电阻,开始时阻值相等,都为R,现将其中一个电阻的阻值增大,将另一个电阻的阻值减小,则两个电阻并联后总电阻将 ( )
A.一定大于R B.一定等于R
C.一定小于R D.以上结果都有可能
4.有两个电阻以一定的方式连接在电压为6 V的电源上,若测得电流为0.5 A,则这两个电阻的阻值及连接方式是 ( )
A.R1=8 Ω R2=4 Ω 并联
B.R1=10 Ω R2=2 Ω 并联
C.R1=20 Ω R2=30 Ω 串联
D.R1=20 Ω R2=30 Ω 并联
5.如图所示,灯泡L1、L2的电阻分别为20 Ω和30 Ω。闭合开关S,通过灯泡L1、L2的电流分别为I1、I2,它们两端的电压分别为U1、U2,则下列选项正确的是 ( )
A.I1∶I2=2∶3 U1∶U2=1∶1
B.I1∶I2=3∶2 U1∶U2=1∶1
C.I1∶I2=1∶1 U1∶U2=2∶3
D.I1∶I2=1∶1 U1∶U2=3∶2
6.将电阻R1和R2并联后接在电源两端,若R1、R2的电阻分别为5 Ω和15 Ω,如图所示,则闭合开关S,电流表A与A1的示数之比为( )
A.3∶1 B.1∶4 C.4∶1 D.4∶3
7.如图所示,电源电压保持不变,先闭合开关S1,电压表示数为U1;再闭合开关S2,电压表示数为U2,则电阻R1、R2的阻值之比为 ( )
A.U1∶U2 B.U2∶UI C.U2∶(U2-U1) D.U1∶(U2-U1)
8.[2019·扬州] 如图所示,电源电压保持不变,开关S闭合后,调节滑动变阻器的滑片,下列说法正确的是(忽略灯丝电阻变化)( )
A.滑片向左滑动,电流表示数增大,电压表示数减小
B.滑片向左滑动,电流表、电压表示数都增大
C.滑片向右滑动,电流表、电压表示数都增大
D.滑片向右滑动,电流表示数减小,电压表示数增大
二、填空题
9.如图所示的电路,电阻R1=R2=4 Ω,电源电压保持不变,当S1、S2都闭合时,电流表的示数为0.8 A,此时电路是 联电路,电路的总电阻是 Ω;当S1闭合、S2断开时,电流表的示数是 A。
10.[2020·郴州] 有阻值相同的三个电阻,以任意方式连接,最多能得到 种不同阻值的电阻;这些不同的连接方式,得到电阻的最大阻值与最小阻值之比是 。
11.在如图所示的电路中,闭合开关S,电流表A1、A2的示数之比为I1∶I2=2∶1,则电阻之比为R1∶R2= ,电流表A1、A3的示数之比为I1∶I3= 。
12.[2019·广安] 如图所示电路中,电源电压恒为6 V,当闭合开关时,电压表的示数为4 V,则灯L2两端电压为 V,灯L1、L2的阻值之比为 。
13.如图所示,电源电压保持不变,只闭合开关S时,电流表的示数为0.2 A,若再闭合开关S1,发现电流表的示数为0.5 A,此时通过R1的电流为I1,通过R2的电流为I2,则I1∶I2为 ,R1∶R2为 。
三、实验探究题
14.[2020·舟山] 在学习了并联电路的特点和欧姆定律后,物理兴趣小组为研究并联电路总电阻和各分电阻之间的关系,开展了以下探究。
[实验步骤]
(1)设计电路,根据如图甲所示的电路图连接图乙实物图(用笔画线代替导线连接)。
(2)闭合开关,分别读出电压表和电流表的示数并记录。
(3)计算总电阻并填入表格。
(4)换用不同规格的电阻重复上述实验。
实验次数 电阻 R1/Ω 电阻 R2/Ω 电压 U/V 电流 I/A 总电阻 R/Ω
1 10 30 3 0.4 7.5
2 30 30 3 0.2 15
3 30 15 3 0.3 10
[得出结论]并联电路总电阻小于任何一个分电阻。
[思考讨论]
(1)请根据影响导体电阻大小的因素解释上述结论: 。
(2)分析表中数据,若增大其中一个分电阻的阻值,则总电阻将 。
四、计算题
15.如图所示的电路中,电源电压U=6 V且保持不变,定值电阻R1=6 Ω,定值电阻R2=4 Ω。求:
(1)只闭合S1时,通过R1的电流是多大。
(2)只闭合S2时,电流表的示数为多少,R2两端的电压是多大。
(3)同时闭合S1、S3时,电流表的示数是多大。
16.[2019·自贡] 已知电源电压不变,为了比较电阻R1和R2的大小,同学们分别设计了如图所示的电路,其中不可行的是 ( )
答案
1.B
2.A 由图可知两电阻并联,当滑片右移时,滑动变阻器接入电路的电阻增大,故电路中的总电阻增大。
3.C 因为并联电路总电阻的倒数等于各支路电阻的倒数之和,所以并联电路的总电阻小于任一支路的电阻值,即两个电阻并联后总电阻小于较小电阻的阻值。
4.D
5.B 两灯并联,灯泡L1、L2的电阻分别为20 Ω和30 Ω,由于并联电路各支路两端的电压相等,故L1、L2两端的电压之比U1∶U2=1∶1;根据I=可知,电压相等时,通过灯泡的电流与灯泡的电阻成反比,则通过灯泡L1、L2的电流之比为I1∶I2=R2∶R1=30 Ω∶20 Ω=3∶2。
6.D 由电路图可知两电阻并联,电流表A测干路电流,电流表A1测R1支路的电流。并联电路具有分流作用,电流的分配与电阻成反比关系,电阻之比R1∶R2=5 Ω∶15 Ω=1∶3,则I1∶I2=3∶1,所以I∶I1=4∶3。
7.D 闭合开关S1、S2时,只有电阻R1连入电路,电压表测量电源电压,则电源电压为U2;只闭合开关S1时,定值电阻R1、R2串联,电压表测量R1两端的电压,则R1两端的电压为U1;因串联电路的总电压等于各部分电路两端电压之和,所以R2两端的电压:U'=U2-U1;串联时通过R1、R2的电流相等,根据欧姆定律可得,R1、R2的阻值之比:===。
8.B 由图可知,灯L与滑动变阻器串联,电压表测量灯L两端的电压;滑片向左滑动,R0减小,电路总电阻减小,电流表和电压表示数均增大,A错误,B正确;滑片向右滑动,R0增大,两表示数均减小,C、D均错误。
9.并 2 0.4
当S1、S2都闭合时,两电阻并联在电路中,电路中的总电阻:R===×4 Ω=2 Ω,电源电压:U=IR=0.8 A×2 Ω=1.6 V;当S1闭合、S2断开时,只有R1接入电路,电路中的电流:I'===0.4 A。
10.7 9∶1 (1)已知三个电阻阻值相同,设一个电阻的阻值为R0,其连接方式可以是:
①一个电阻接入电路,电路总电阻为R1=R0;
②两个电阻串联接入电路,电路总电阻为R2=2R0;
③两个电阻并联接入电路,电路总电阻为R3=R0;
④三个电阻串联接入电路,电路总电阻为R4=3R0;
⑤三个电阻并联接入电路,电路总电阻为R5=R0;
⑥两个电阻先串联再与第三个电阻并联接入电路,电路总电阻为R6=R0;
⑦两个电阻先并联再与第三个电阻串联接入电路,电路总电阻为R7=R0。
所以阻值相同的三个电阻,以任意方式连接,最多能得到7种不同阻值的电阻。
(2)由以上分析知,三个电阻串联接入电路,电路总电阻最大,为R4=3R0;
三个电阻并联接入电路,电路总电阻最小,为R5=R0,
所以得到电阻的最大阻值与最小阻值之比是=。
11.1∶2 2∶3 由电路图可知,电阻R1、R2并联,电流表A1测通过电阻R1的电流,电流表A2测通过电阻R2的电流,电流表A3测干路中的电流,根据并联电路的分流规律可得,R1∶R2=I2∶I1=1∶2;因并联电路干路中的电流等于各支路电流之和,所以,电流表A1、A3的示数之比为===。
12.2 2∶1 由图可知两灯泡串联,则U=U1+U2,且=,电压表测L1两端的电压,即U1=4 V,则U2=U-U1=6 V-4 V=2 V,可得===2∶1。
13.3∶2 2∶3
14.[实验步骤](1)如图图所示
[思考讨论](1)并联后相当于增大了导体的横截面积,在导体材料、长度、温度不变时,导体的横截面积越大,导体的电阻越小
(2)增大
15.(1)由电路图可知,只闭合S1时,只有电阻R1接入电路,通过R1的电流:I1===1 A。
(2)由电路图可知,只闭合S2时,两电阻串联,R1、R2串联的总电阻:R=R1+R2=6 Ω+4 Ω=10 Ω,电路中的电流:I===0.6 A,即电流表的示数为0.6 A。
由欧姆定律I=得,R2两端的电压:
U2=IR2=0.6 A×4 Ω=2.4 V。
(3)同时闭合S1、S3时,R1、R2并联,电流表测干路中的电流,则通过R1的电流:I1'===1 A。通过R2的电流:I2'===1.5 A,则干路电流:I'=I1'+I2'=1 A+1.5 A=2.5 A,即电流表的示数为2.5 A。
16.A 图A中两电阻并联,电压表测电源电压,电流表测量干路电流,只能测出电路的总电阻,不能比较通过电阻R2、R1的电流大小,因此无法比较两电阻阻值的大小,故A符合题意;图B中两电阻串联,两个电压表分别测量两个电阻两端的电压,由于通过两电阻的电流相等,根据电压的大小就可以比较出电阻的大小,故B不符合题意;图C中开关闭合时电路为R1的简单电路,开关断开时两电阻串联,电流表测电路中的电流,根据串联电路的特点和欧姆定律分别表示出电源电压,利用电源电压不变建立等式,通过比较电流之间的关系得出电阻的大小关系,故C不符合题意;图D中两个电阻串联,电压表V1测量串联电阻的总电压,电压表V2测量电阻R1两端的电压,根据串联电路电压的规律,电阻R2两端的电压等于电压表V1和V2的示数之差,这样就可以得到两个电阻两端的电压,根据电压的大小就可以比较电阻的大小,故D不符合题意。
同课章节目录
- 第十一章 机械功与机械能
- 11.1 怎样才叫做功
- 11.2 怎样比较做功的快慢
- 11.3 如何提高机械效率
- 11.4 认识动能和势能
- 第十二章 内能与热机
- 12.1 认识内能
- 12.2 热量和热值
- 12.3 研究物质的比热容
- 12.4 热机与社会发展
- 第十三章 探究简单电路
- 13.1 从闪电谈起
- 13.2 电路的组成和连接方式
- 13.3 怎样认识和测量电流
- 13.4 探究串、并联电路中的电流
- 13.5 怎样认识和测量电压
- 13.6 探究串、并联电路中的电压
- 第十四章 探究欧姆定律
- 14.1 怎样认识电阻
- 14.2 探究欧姆定律
- 14.3 欧姆定律的应用
- 第十五章 电能与电功率
- 15.1 电能与电功
- 15.2 认识电功率
- 15.3 怎样使用电器正常工作
- 15.4 探究焦耳定律
