18.4 一元二次方程的根与系数的关系
文档属性
| 名称 | 18.4 一元二次方程的根与系数的关系 |  | |
| 格式 | zip | ||
| 文件大小 | 321.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-08-17 15:12:45 | ||
图片预览






文档简介
课件17张PPT。18.4 一元二次方程的根与系数的关系(1)一元二次方程的一般形式是什么ax2+bx+c=0(a≠0) (2)一元二次方程的根的判别式是什么判别式的值 根的情况 判别式的值 根的情况
△ ≥0 有两个实根
△<0 没有实数根 △ >0 有两个不相等的实根
△=0 有两个相等的实根
△<0 没有实数根
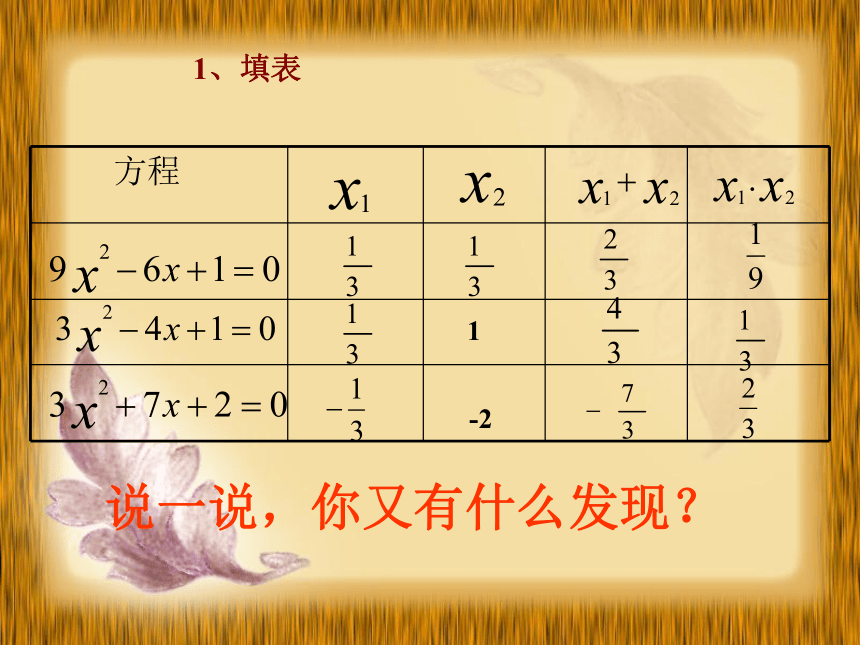
1-21、填表说一说,你又有什么发现?结论返回
如果一元二次方程ax2+bx+c=0(a≠0)
的两个根是x1,x2 ,那么
推理论证 Δ≥0练习1.(口答)下列方程中,
两根的和与两根的积各是多少?
(1)
(2)
(3)
(4)
(5)
(6) 练一练·一元二次方程根与系数关系的应用 (1)验根。 (口答)判定下列各方程后面的两个数是不是它
的两个根。 ;
④(2)已知方程一根,求另一根。 例:已知方程5x2+kx-6=0的根是2,
求它的另一根及k的值。 方法(一)
? ∵? 2是方程 的根,
∴?
∴? 原方程可化为
解得: {例:已知方程5x2+kx-6=0的根是2,
求它的另一根及k的值。 {18.4 一元二次方程的根与系数的关系1.已知一元二次方程的 两
根分别为 ,则:2.已知一元二次方程的 两根
分别为 ,则:3.已知一元二次方程的
的一个根为1 ,则方程的另一根为___,
m=___:4.已知一元二次方程的 两
根分别为 -2 和 1 ,则:p =__ ; q=__2-1-2261-2结 论:特 例:公式的应用: 例1、利用根与系数的关系,求一元二次方程 2x2+3x -1=0 两个根的:(1)平方和;(2)倒数和解:设方程的两个根是x1 , x2. 1、设 x1 、 x2是方程 2x2+4x =3 利用根与系数的 关系,求下列各式的值:
2、已知方程 x2=2x+1的两根为x1 , x2,不解方程,求下列各式的值。
(1)(x1-x2)2 (2)x13x2+x1x23 练习:例2:已知方程kx2 -(2k-1) x + k-2=0 的两根为x1 、 x2, 且 x12 + x22 =3 ,
求k的值。例题: 例3:方程x2 ? (m?1)x ?2m ?1?0求m满足什么条件时,方程的两根互为相反数?方程的两根互为倒数?方程的一根为零?例题:引申:
若 ax2?bx?c?0 (a?0 ??0)
(1)若两根互为相反数,则b ? 0;
(2)若两根互为倒数,则a ? c;
(3)若一根为0,则c ? 0 ;
(4)若一根为1,则a ? b ?c ? 0 ;
(5)若一根为?1,则a ? b ? c ? 0;
(6)若a、c异号,方程一定有两个实数根.
△ ≥0 有两个实根
△<0 没有实数根 △ >0 有两个不相等的实根
△=0 有两个相等的实根
△<0 没有实数根
1-21、填表说一说,你又有什么发现?结论返回
如果一元二次方程ax2+bx+c=0(a≠0)
的两个根是x1,x2 ,那么
推理论证 Δ≥0练习1.(口答)下列方程中,
两根的和与两根的积各是多少?
(1)
(2)
(3)
(4)
(5)
(6) 练一练·一元二次方程根与系数关系的应用 (1)验根。 (口答)判定下列各方程后面的两个数是不是它
的两个根。 ;
④(2)已知方程一根,求另一根。 例:已知方程5x2+kx-6=0的根是2,
求它的另一根及k的值。 方法(一)
? ∵? 2是方程 的根,
∴?
∴? 原方程可化为
解得: {例:已知方程5x2+kx-6=0的根是2,
求它的另一根及k的值。 {18.4 一元二次方程的根与系数的关系1.已知一元二次方程的 两
根分别为 ,则:2.已知一元二次方程的 两根
分别为 ,则:3.已知一元二次方程的
的一个根为1 ,则方程的另一根为___,
m=___:4.已知一元二次方程的 两
根分别为 -2 和 1 ,则:p =__ ; q=__2-1-2261-2结 论:特 例:公式的应用: 例1、利用根与系数的关系,求一元二次方程 2x2+3x -1=0 两个根的:(1)平方和;(2)倒数和解:设方程的两个根是x1 , x2. 1、设 x1 、 x2是方程 2x2+4x =3 利用根与系数的 关系,求下列各式的值:
2、已知方程 x2=2x+1的两根为x1 , x2,不解方程,求下列各式的值。
(1)(x1-x2)2 (2)x13x2+x1x23 练习:例2:已知方程kx2 -(2k-1) x + k-2=0 的两根为x1 、 x2, 且 x12 + x22 =3 ,
求k的值。例题: 例3:方程x2 ? (m?1)x ?2m ?1?0求m满足什么条件时,方程的两根互为相反数?方程的两根互为倒数?方程的一根为零?例题:引申:
若 ax2?bx?c?0 (a?0 ??0)
(1)若两根互为相反数,则b ? 0;
(2)若两根互为倒数,则a ? c;
(3)若一根为0,则c ? 0 ;
(4)若一根为1,则a ? b ?c ? 0 ;
(5)若一根为?1,则a ? b ? c ? 0;
(6)若a、c异号,方程一定有两个实数根.
