20.3 矩形 菱形 正方形
图片预览







文档简介
课件77张PPT。20.3 矩形 菱形 正方形第一课时矩形的定义有一个角是直角的平行四边形是矩形矩形的定义:对边平行, 对边相等;
对角相等,邻角互补;
对角线互相平分矩形: 有一个角是直角的平行四
边形是矩形
特殊的平行四边形 一般性质:
具备平行四边形所有的性质探索新知:
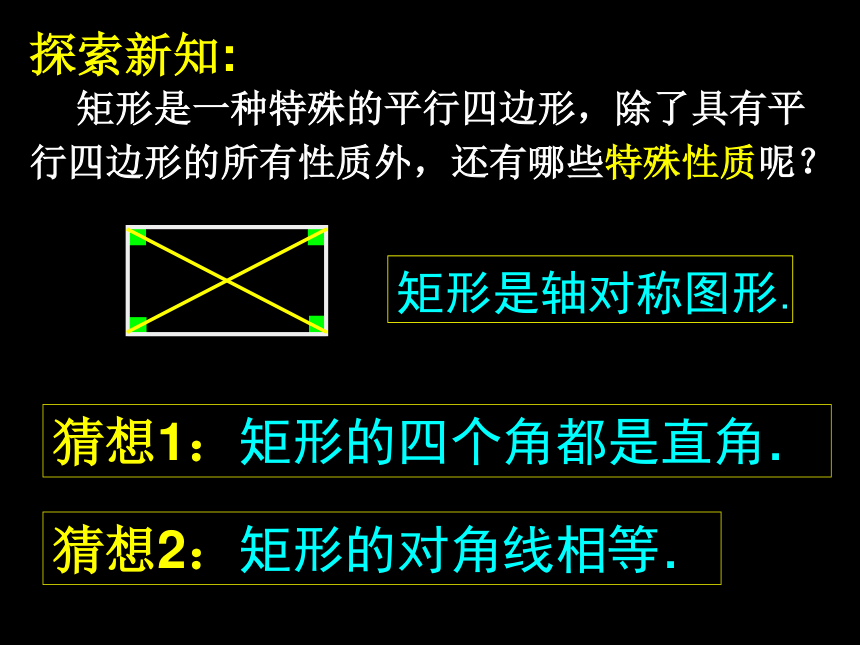
矩形是一种特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?矩形是轴对称图形.探索新知:
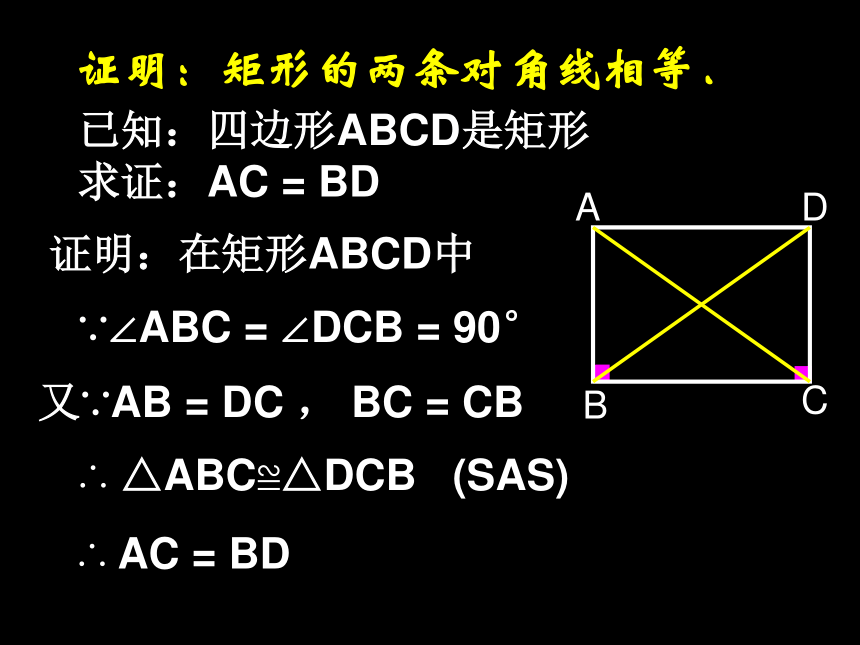
矩形是一种特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.矩形是轴对称图形.已知:四边形ABCD是矩形
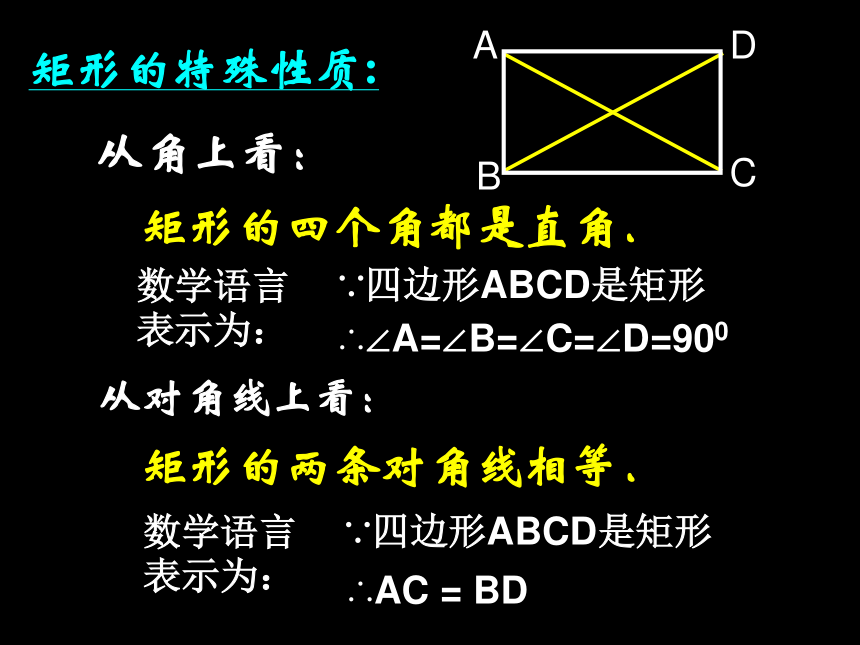
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴ △ABC≌△DCB (SAS)∴ AC = BD证明:矩形的两条对角线相等.矩形的特殊性质:矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:数学语言表示为:∵四边形ABCD是矩形 ∴∠A=∠B=∠C=∠D=900数学语言表示为:∵四边形ABCD是矩形 ∴AC = BDwww.zk5u.comOABCD公平,因为OA=OC=OB=OD生活链接---投圈游戏www.zk5u.com 已知:在Rt△ABC中,∠ABC=900,BO是AC上的中线.
求证: BO = AC
OD证明: 延长BO至D,使OD=BO,
连结AD、DC.∵AO=OC, BO=OD
∴四边形ABCD是平行四边形. ∵∠ABC=900∴AC=BD再探新知:推论:
直角三角形斜边上的中线
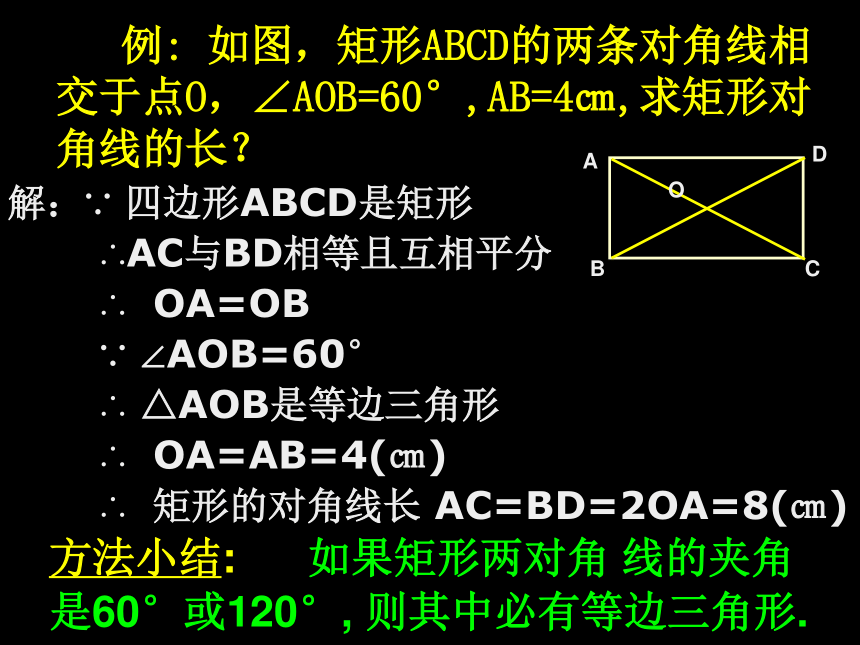
等于斜边的一半. O 例: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长? 解:∵ 四边形ABCD是矩形
∴AC与BD相等且互相平分
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4(㎝)
∴ 矩形的对角线长 AC=BD=2OA=8(㎝)O方法小结: 如果矩形两对角 线的夹角是60°或120°, 则其中必有等边三角形. 20.3 矩形 菱形 正方形第二课时矩形的判定矩形的四个角都是直角.※ 矩形的性质定理1矩形的对角线相等.※ 矩形的性质定理2※ 推 论 直角三角形斜边上的中线等于斜边的一半. 矩形具有而一般平行四边形不
具有的性质是 ( ) A.对角相等B.对边相等C.对角线相等 D.对角线互相平分C课前热身四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=____ ㎝ ,OB=___ ㎝
2.若已知AC=10㎝,BC=6㎝,则矩形的周长=____ cm, 矩形的面积=___ ㎝2
若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm, AB= _____cm51044828课前热身 4.已知△ABC是Rt△,∠ABC=900,
BD是斜边AC上的中线(1) 若BD=3㎝则AC= ㎝
(2) 若∠C=30°, AB=5㎝,则AC= ㎝,
BD= ㎝.6510课前热身2、 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?解: ∵ △AOB、 △BOC、 △COD
和△AOD四个三角形的周长和为86cm,
又∵AC=BD=13cm,∴ AB+BC+CD+DA=86-2(AC+BD)=86-4×13=34(cm)即矩形ABCD的周长等于34cm。O 工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?情境一:猜想:
对角线相等的平行
四边形是矩形 .命题:对角线相等的平行四边形是矩形已知:平行四边形ABCD中,AC = BD.
求证:四边形ABCD是矩形.证明: ∵ AB=CD, BC=BC, AC=BD∴ △ABC≌ △DCB(SSS)∵ AB//CD
∴ ∠ABC+∠DCB=180° ∴ ∠ABC=∠DCB=90°
又 ∵ 四边形ABCD是平行四边形∴四边形ABCD是矩形∴ ∠ABC = ∠DCB对角线相等的平行四边形是矩形 .矩形的判定方法1:几何语言:∵四边形ABCD是平行四边形
AC=BD∴四边形ABCD是矩形(对角线相等且互相平分的四边形是矩形.)(或OA=OC=OB=OD) 例3:已知,如图.矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO的中点,
求证:四边形EFGH是矩形. 情境一:李芳同学有“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?猜想:有三个角是直角的四边形是矩形 你能证明上述结论吗?矩形的判定方法2:有三个角是直角的四边形是矩形 . ∵ ∠A = B =∠C = 90°
∴四边形ABCD是矩形几何语言:20.3 矩形 菱形 正方形第三课时矩形的判定你能归纳矩形的几种判定方法吗?有一个角是直角的平行四边形是矩形.对角线相等的平行四边形是矩形 .(对角线相等且互相平分的四边形是矩形.)有三个角是直角的四边形是矩形 .定义:矩形判定定理1:矩形判定定理2:下列各句判定矩形的说法是否正确?(1)对角线相等的四边形是矩形;(2)对角线互相平分且相等的四边形是矩形;(3)有一个角是直角的四边形是矩形;(5)有三个角是直角的四边形是矩形;(6)四个角都相等的四边形是矩形;(7)对角线相等,且有一个角是直角的四边形是矩形;(10)一组邻边垂直,一组对边平行且相等的四边形是
矩形;(9)对角线相等且互相垂直的四边形是矩形;(8)一组对角互补的平行四边形是矩形;(4)有三个角都相等的四边形是矩形;XXXX 1.如图, ABCD中,AB=6, BC=8, AC=10.
求证: 四边形ABCD是矩形. 2.已知:如图在 ABCD中,M为BC中点,
∠MAD=∠MDA.
求证:四边形 ABCD是矩形. 3. 如图,△ABC中,AB=AC, AD、AE分别是∠A与∠A的外角的平分线,BE⊥AE.
求证: AB=DE. 4.已知:如图,BC是等腰△BED底边ED上的高,四边形ABEC是平行四边形.
求证:四边形ABCD是矩形.20.3 矩形 菱形 正方形第四课时菱形两组对边
分别平行矩形情景创设我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,我们已经研究了一种特殊的平行四边形——矩形 ;这堂课还要研究另一种特殊的平行四边形——菱形有一个角是直角菱形有一组邻边相等有一组邻边相等的平行四边形叫做菱形;菱形的定义: 我们可以这样做:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗? 如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?菱形的性质:(1)菱形具有平行四边形的一切性质;(2)菱形的四条边都相等;(3)菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角;已知:如图:菱形ABCD的对角线AC和BD相交于点证明:∵四边形ABCD是菱形 在△ABD中,
又 ∵BO=DO∴AB=AD(菱形的四条边都相等)∴AC⊥BD,AC平分∠BAD同理: AC平分∠BCD;
BD平分∠ABC和∠ADC求证:AC⊥BD ;AC平分∠BAD和∠BCD;BD
平分∠ABC和∠ADC 命题:菱形的对角线互相垂直平分,
并且每一条对角线平分一组对角;相等的线段:相等的角:等腰三角形有:直角三角形有:全等三角形有:已知四边形ABCD是菱形AB=CD=AD=BC
OA=OC OB=OD∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOARt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACDABCDO12345678菱形的 两条对角线互相平分菱形的两组对边平行且相等边对角线角菱形的性质:菱形的四条边相等菱形的两组对角分别相等菱形的邻角互补 菱形的两条对角线互相垂直, 每一条对角线平分一组对角【菱形的面积公式】OE S菱形 = BC·AE 思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗? 菱形的面积=底×高=对角线乘积的一半学以致用: 1.已知菱形的周长是12cm,那么它的边长是______. 2.菱形ABCD中∠ABC=60 °则∠BAC=_______.3cm60 ° 3.菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两对角线AC、BD的长。 4.菱形ABCD中两条对角线的长分别是6cm和8cm,求菱形的周长和面积. 例1:已知菱形ABCD中,E是AB的中点,且
DE⊥AB,AB=4.
求:⑴∠ABC的度数
⑵对角线AC的长
⑶菱形ABCD的面积例2:如图,E为菱形ABCD边BC上一点,且
AB=AE,AE交BD于O,且∠ DAE=2∠BAE,
求证:EB=OA;练习:
1.已知,菱形对角线长分别为12cm和16cm,求菱形的高。2.在菱形ABCD中,AE⊥BC,AF⊥CD,
E、F分别为BC,CD的中点,那么
∠EAF的度数是( )A.75°B.60°C.45°D.30°B 例3:已知:如图,AD平分∠BAC, DE∥AC交AB于E,DF∥AB交AC于F.
求证:EF⊥AD 20.3 矩形 菱形 正方形第五课时菱形知识回顾:菱形的定义:有一组邻边相等的平行四边形是菱形菱形的性质:1. 菱形的两组对边平行,四条边相等2. 菱形的两组对角分别相等,邻角互补3. 菱形的两条对角线互相垂直平分, 且
每一条对角线平分一组对角思 考:
除了运用菱形的定义,类比研究平行四边形和举行的性质和判定,你能找出判定菱形的其他方法吗?猜 想:
对角线互相垂直的平行四边形是菱形.
证明:
对角线互相垂直的平行四边形是菱形.已知:平行四边形ABCD中,对角线
AC、BD互相垂直.
求证:四边形ABCD是菱形.
菱形的判定定理1:
对角线互相垂直的平行四边形是菱形. 例4:如图,已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F.
求证:四边形AFCE是菱形.
猜 想:
四条边都相等的四边形是菱形.已知:如图,四边形ABCD中,
AB=BC=CD=DA
求证:四边形ABCD是菱形菱形的判定定理2:
四条边都相等的四边形是菱形.猜 想:
如果一个四边形的每条对角线平分一组对角,那么这个四边形是菱形.已知:如图, AC平分∠DAB和∠DCB,
BD平分∠ABC和∠ADC
求证:四边形ABCD是菱形菱形的判定定理3:
每条对角线平分一组对角的四边形是菱形.课堂小结:
判定四边形是菱形共有哪几种方法?菱形的判定定理1:
对角线互相垂直的平行四边形是菱形.菱形的判定定理3:
每条对角线平分一组对角的四边形是菱形.菱形的判定定理2:
四条边都相等的四边形是菱形.20.3 矩形 菱形 正方形第六课时菱形知识回顾:菱形的定义:有一组邻边相等的平行四边形是菱形菱形的性质:1. 菱形的两组对边平行,四条边相等2. 菱形的两组对角分别相等,邻角互补3. 菱形的两条对角线互相垂直平分, 且
每一条对角线平分一组对角判定四边形是菱形有哪几种方法?菱形的判定定理1:
对角线互相垂直的平行四边形是菱形.菱形的判定定理3:
每条对角线平分一组对角的四边形是菱形.菱形的判定定理2:
四条边都相等的四边形是菱形.知识回顾: 做一做:判断下列命题是否正确,并说明理由.
① 对角线互相平分且邻边相等的四边形是菱形.
② 两组对边分别平行且一组邻边相等的四边形
是菱形.
③ 邻角相等的四边形是菱形.
④ 有一组邻边相等的四边形是菱形.
⑤ 两组对角分别相等且对角线互相垂直的四边形
是菱形.
⑥ 对角线互相垂直的四边形是菱形.
⑦ 对角线互相垂直平分的四边形是菱形.
⑧ 一条对角线平分一个内角的平行四边形是菱形. 错对对对错对错对 例5:已知:如图,△ABC中,∠BAC的平分线交BC于点D,E是AB上一点,且AE=AC,EF∥BC交AD于点F.
求证:四边形CDEF是菱形 例6:已知:如图,在菱形ABCD中,E、F分别是BC、CD上的点,且CE=CF。过点C作CG∥EA交AF于H,交AD于G,若∠BAE=25°,∠BCD=130°,求∠AHC的度数. 例7:已知:如图,C是线段BD上一点,△ABC和△ECD都是等边三角形,R、F、G、H分别是四边形ABDE各边的中点.
求证:四边形RFGH是菱形 如图,边长为a的菱形ABCD中,∠DAB=60度,E是异于A、D两点的动点,F是CD上的动点,满足AE + CF = a .
证明:不论E、F怎样移动, △BEF总是正三角形。20.3 矩形 菱形 正方形第七课时正方形
矩形的性质:
1. 矩形是轴对称图形.2. 矩形的四个内角都是直角.3. 矩形的对角线相等且互相平分.矩形的判定方法:1. 有一个角是直角的平行四边形是矩形.2. 对角线相等的平行四边形是矩形.3. 有三个角是直角的四边形是矩形.复习巩固:矩形的概念:
有一个角是直角的平行四边形是矩形菱形的概念:
一组邻边相等的平行四边形是菱形.菱形的性质:1. 菱形是轴对称图形.2. 菱形的四条边都相等.3. 菱形的两条对角线互相垂直平分,并且
分别平分每一组对角.菱形的判定方法:2. 四条边都相等的四边形是菱形.1. 有一组邻边相等的平行四边形是菱形.3. 对角线互相垂直的平行四边形是菱形.复习巩固:4.每条对角线平分一组对角的四边形是菱形.画一画,猜一猜 请同学们画一个四边形,
要求它既是矩形又是菱形.正方形的定义 : 有一个角是直角, 且有一组邻边相等的平行四边形叫做正方形.观察图形,你能发现正方形有哪些性质吗?正方形的性质:边----角----对角线----对边平行,四边相等四个角都是直角对角线相等且互相垂直平分,每一条对角线平分一组对角是轴对称图形,对称轴有四条.对称性----根据图形所具有的性质,在下表相应的空格中打 ”√”√√√√√√ √√√√√√√√√√平行四边形矩形菱形正方形平行四边形、矩形、菱形、正方形的关系图矩 形菱 形正方形有一组邻边相等有一个角是直角探究活动: 判断满足下列条件的四边形是否是正方形?并说明理由.
① 对角线互相垂直且相等的平行四边形.
② 对角线互相垂直的矩形.
③ 对角线相等的菱形.
④ 对角线互相垂直平分且相等的四边形.① 有一个角是直角的菱形是正方形.
② 有一组邻边相等的矩形是正方形.
③ 对角线相等的菱形是正方形.
④ 对角线互相垂直的矩形是正方形.
对角线互相垂直平分且相等的四
边形是正方形.正方形的判定方法: 例8.已知:正方形ABCD中,点A1、B1、C1、D1分别在AB 、BC 、CD 、DA上,且AA1=BB1=CC1=DD1,试判断四边形A1B1C1D1是正方形吗?为什么?证明四个三角形全等证明四边形A1B1C1D1为菱形证明四边形A1B1C1D1为正方形分
析小 结: 课堂小结:一、正方形的性质1. 正方形是特殊的平行四边形,具备平行
四边形的所有性质.
2. 正方形是特殊的矩形和菱形,具备它们
的所有特征.3. 正方形的四条边都相等.4. 正方形的两条对角线互相垂直平分且相
等,并且分别平分每一组对角.5. 正方形即是轴对称图形.二、正方形的判定
对角相等,邻角互补;
对角线互相平分矩形: 有一个角是直角的平行四
边形是矩形
特殊的平行四边形 一般性质:
具备平行四边形所有的性质探索新知:
矩形是一种特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?矩形是轴对称图形.探索新知:
矩形是一种特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.矩形是轴对称图形.已知:四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴ △ABC≌△DCB (SAS)∴ AC = BD证明:矩形的两条对角线相等.矩形的特殊性质:矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:数学语言表示为:∵四边形ABCD是矩形 ∴∠A=∠B=∠C=∠D=900数学语言表示为:∵四边形ABCD是矩形 ∴AC = BDwww.zk5u.comOABCD公平,因为OA=OC=OB=OD生活链接---投圈游戏www.zk5u.com 已知:在Rt△ABC中,∠ABC=900,BO是AC上的中线.
求证: BO = AC
OD证明: 延长BO至D,使OD=BO,
连结AD、DC.∵AO=OC, BO=OD
∴四边形ABCD是平行四边形. ∵∠ABC=900∴AC=BD再探新知:推论:
直角三角形斜边上的中线
等于斜边的一半. O 例: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长? 解:∵ 四边形ABCD是矩形
∴AC与BD相等且互相平分
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4(㎝)
∴ 矩形的对角线长 AC=BD=2OA=8(㎝)O方法小结: 如果矩形两对角 线的夹角是60°或120°, 则其中必有等边三角形. 20.3 矩形 菱形 正方形第二课时矩形的判定矩形的四个角都是直角.※ 矩形的性质定理1矩形的对角线相等.※ 矩形的性质定理2※ 推 论 直角三角形斜边上的中线等于斜边的一半. 矩形具有而一般平行四边形不
具有的性质是 ( ) A.对角相等B.对边相等C.对角线相等 D.对角线互相平分C课前热身四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=____ ㎝ ,OB=___ ㎝
2.若已知AC=10㎝,BC=6㎝,则矩形的周长=____ cm, 矩形的面积=___ ㎝2
若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm, AB= _____cm51044828课前热身 4.已知△ABC是Rt△,∠ABC=900,
BD是斜边AC上的中线(1) 若BD=3㎝则AC= ㎝
(2) 若∠C=30°, AB=5㎝,则AC= ㎝,
BD= ㎝.6510课前热身2、 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?解: ∵ △AOB、 △BOC、 △COD
和△AOD四个三角形的周长和为86cm,
又∵AC=BD=13cm,∴ AB+BC+CD+DA=86-2(AC+BD)=86-4×13=34(cm)即矩形ABCD的周长等于34cm。O 工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?情境一:猜想:
对角线相等的平行
四边形是矩形 .命题:对角线相等的平行四边形是矩形已知:平行四边形ABCD中,AC = BD.
求证:四边形ABCD是矩形.证明: ∵ AB=CD, BC=BC, AC=BD∴ △ABC≌ △DCB(SSS)∵ AB//CD
∴ ∠ABC+∠DCB=180° ∴ ∠ABC=∠DCB=90°
又 ∵ 四边形ABCD是平行四边形∴四边形ABCD是矩形∴ ∠ABC = ∠DCB对角线相等的平行四边形是矩形 .矩形的判定方法1:几何语言:∵四边形ABCD是平行四边形
AC=BD∴四边形ABCD是矩形(对角线相等且互相平分的四边形是矩形.)(或OA=OC=OB=OD) 例3:已知,如图.矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO的中点,
求证:四边形EFGH是矩形. 情境一:李芳同学有“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?猜想:有三个角是直角的四边形是矩形 你能证明上述结论吗?矩形的判定方法2:有三个角是直角的四边形是矩形 . ∵ ∠A = B =∠C = 90°
∴四边形ABCD是矩形几何语言:20.3 矩形 菱形 正方形第三课时矩形的判定你能归纳矩形的几种判定方法吗?有一个角是直角的平行四边形是矩形.对角线相等的平行四边形是矩形 .(对角线相等且互相平分的四边形是矩形.)有三个角是直角的四边形是矩形 .定义:矩形判定定理1:矩形判定定理2:下列各句判定矩形的说法是否正确?(1)对角线相等的四边形是矩形;(2)对角线互相平分且相等的四边形是矩形;(3)有一个角是直角的四边形是矩形;(5)有三个角是直角的四边形是矩形;(6)四个角都相等的四边形是矩形;(7)对角线相等,且有一个角是直角的四边形是矩形;(10)一组邻边垂直,一组对边平行且相等的四边形是
矩形;(9)对角线相等且互相垂直的四边形是矩形;(8)一组对角互补的平行四边形是矩形;(4)有三个角都相等的四边形是矩形;XXXX 1.如图, ABCD中,AB=6, BC=8, AC=10.
求证: 四边形ABCD是矩形. 2.已知:如图在 ABCD中,M为BC中点,
∠MAD=∠MDA.
求证:四边形 ABCD是矩形. 3. 如图,△ABC中,AB=AC, AD、AE分别是∠A与∠A的外角的平分线,BE⊥AE.
求证: AB=DE. 4.已知:如图,BC是等腰△BED底边ED上的高,四边形ABEC是平行四边形.
求证:四边形ABCD是矩形.20.3 矩形 菱形 正方形第四课时菱形两组对边
分别平行矩形情景创设我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,我们已经研究了一种特殊的平行四边形——矩形 ;这堂课还要研究另一种特殊的平行四边形——菱形有一个角是直角菱形有一组邻边相等有一组邻边相等的平行四边形叫做菱形;菱形的定义: 我们可以这样做:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗? 如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?菱形的性质:(1)菱形具有平行四边形的一切性质;(2)菱形的四条边都相等;(3)菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角;已知:如图:菱形ABCD的对角线AC和BD相交于点证明:∵四边形ABCD是菱形 在△ABD中,
又 ∵BO=DO∴AB=AD(菱形的四条边都相等)∴AC⊥BD,AC平分∠BAD同理: AC平分∠BCD;
BD平分∠ABC和∠ADC求证:AC⊥BD ;AC平分∠BAD和∠BCD;BD
平分∠ABC和∠ADC 命题:菱形的对角线互相垂直平分,
并且每一条对角线平分一组对角;相等的线段:相等的角:等腰三角形有:直角三角形有:全等三角形有:已知四边形ABCD是菱形AB=CD=AD=BC
OA=OC OB=OD∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOARt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACDABCDO12345678菱形的 两条对角线互相平分菱形的两组对边平行且相等边对角线角菱形的性质:菱形的四条边相等菱形的两组对角分别相等菱形的邻角互补 菱形的两条对角线互相垂直, 每一条对角线平分一组对角【菱形的面积公式】OE S菱形 = BC·AE 思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗? 菱形的面积=底×高=对角线乘积的一半学以致用: 1.已知菱形的周长是12cm,那么它的边长是______. 2.菱形ABCD中∠ABC=60 °则∠BAC=_______.3cm60 ° 3.菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两对角线AC、BD的长。 4.菱形ABCD中两条对角线的长分别是6cm和8cm,求菱形的周长和面积. 例1:已知菱形ABCD中,E是AB的中点,且
DE⊥AB,AB=4.
求:⑴∠ABC的度数
⑵对角线AC的长
⑶菱形ABCD的面积例2:如图,E为菱形ABCD边BC上一点,且
AB=AE,AE交BD于O,且∠ DAE=2∠BAE,
求证:EB=OA;练习:
1.已知,菱形对角线长分别为12cm和16cm,求菱形的高。2.在菱形ABCD中,AE⊥BC,AF⊥CD,
E、F分别为BC,CD的中点,那么
∠EAF的度数是( )A.75°B.60°C.45°D.30°B 例3:已知:如图,AD平分∠BAC, DE∥AC交AB于E,DF∥AB交AC于F.
求证:EF⊥AD 20.3 矩形 菱形 正方形第五课时菱形知识回顾:菱形的定义:有一组邻边相等的平行四边形是菱形菱形的性质:1. 菱形的两组对边平行,四条边相等2. 菱形的两组对角分别相等,邻角互补3. 菱形的两条对角线互相垂直平分, 且
每一条对角线平分一组对角思 考:
除了运用菱形的定义,类比研究平行四边形和举行的性质和判定,你能找出判定菱形的其他方法吗?猜 想:
对角线互相垂直的平行四边形是菱形.
证明:
对角线互相垂直的平行四边形是菱形.已知:平行四边形ABCD中,对角线
AC、BD互相垂直.
求证:四边形ABCD是菱形.
菱形的判定定理1:
对角线互相垂直的平行四边形是菱形. 例4:如图,已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F.
求证:四边形AFCE是菱形.
猜 想:
四条边都相等的四边形是菱形.已知:如图,四边形ABCD中,
AB=BC=CD=DA
求证:四边形ABCD是菱形菱形的判定定理2:
四条边都相等的四边形是菱形.猜 想:
如果一个四边形的每条对角线平分一组对角,那么这个四边形是菱形.已知:如图, AC平分∠DAB和∠DCB,
BD平分∠ABC和∠ADC
求证:四边形ABCD是菱形菱形的判定定理3:
每条对角线平分一组对角的四边形是菱形.课堂小结:
判定四边形是菱形共有哪几种方法?菱形的判定定理1:
对角线互相垂直的平行四边形是菱形.菱形的判定定理3:
每条对角线平分一组对角的四边形是菱形.菱形的判定定理2:
四条边都相等的四边形是菱形.20.3 矩形 菱形 正方形第六课时菱形知识回顾:菱形的定义:有一组邻边相等的平行四边形是菱形菱形的性质:1. 菱形的两组对边平行,四条边相等2. 菱形的两组对角分别相等,邻角互补3. 菱形的两条对角线互相垂直平分, 且
每一条对角线平分一组对角判定四边形是菱形有哪几种方法?菱形的判定定理1:
对角线互相垂直的平行四边形是菱形.菱形的判定定理3:
每条对角线平分一组对角的四边形是菱形.菱形的判定定理2:
四条边都相等的四边形是菱形.知识回顾: 做一做:判断下列命题是否正确,并说明理由.
① 对角线互相平分且邻边相等的四边形是菱形.
② 两组对边分别平行且一组邻边相等的四边形
是菱形.
③ 邻角相等的四边形是菱形.
④ 有一组邻边相等的四边形是菱形.
⑤ 两组对角分别相等且对角线互相垂直的四边形
是菱形.
⑥ 对角线互相垂直的四边形是菱形.
⑦ 对角线互相垂直平分的四边形是菱形.
⑧ 一条对角线平分一个内角的平行四边形是菱形. 错对对对错对错对 例5:已知:如图,△ABC中,∠BAC的平分线交BC于点D,E是AB上一点,且AE=AC,EF∥BC交AD于点F.
求证:四边形CDEF是菱形 例6:已知:如图,在菱形ABCD中,E、F分别是BC、CD上的点,且CE=CF。过点C作CG∥EA交AF于H,交AD于G,若∠BAE=25°,∠BCD=130°,求∠AHC的度数. 例7:已知:如图,C是线段BD上一点,△ABC和△ECD都是等边三角形,R、F、G、H分别是四边形ABDE各边的中点.
求证:四边形RFGH是菱形 如图,边长为a的菱形ABCD中,∠DAB=60度,E是异于A、D两点的动点,F是CD上的动点,满足AE + CF = a .
证明:不论E、F怎样移动, △BEF总是正三角形。20.3 矩形 菱形 正方形第七课时正方形
矩形的性质:
1. 矩形是轴对称图形.2. 矩形的四个内角都是直角.3. 矩形的对角线相等且互相平分.矩形的判定方法:1. 有一个角是直角的平行四边形是矩形.2. 对角线相等的平行四边形是矩形.3. 有三个角是直角的四边形是矩形.复习巩固:矩形的概念:
有一个角是直角的平行四边形是矩形菱形的概念:
一组邻边相等的平行四边形是菱形.菱形的性质:1. 菱形是轴对称图形.2. 菱形的四条边都相等.3. 菱形的两条对角线互相垂直平分,并且
分别平分每一组对角.菱形的判定方法:2. 四条边都相等的四边形是菱形.1. 有一组邻边相等的平行四边形是菱形.3. 对角线互相垂直的平行四边形是菱形.复习巩固:4.每条对角线平分一组对角的四边形是菱形.画一画,猜一猜 请同学们画一个四边形,
要求它既是矩形又是菱形.正方形的定义 : 有一个角是直角, 且有一组邻边相等的平行四边形叫做正方形.观察图形,你能发现正方形有哪些性质吗?正方形的性质:边----角----对角线----对边平行,四边相等四个角都是直角对角线相等且互相垂直平分,每一条对角线平分一组对角是轴对称图形,对称轴有四条.对称性----根据图形所具有的性质,在下表相应的空格中打 ”√”√√√√√√ √√√√√√√√√√平行四边形矩形菱形正方形平行四边形、矩形、菱形、正方形的关系图矩 形菱 形正方形有一组邻边相等有一个角是直角探究活动: 判断满足下列条件的四边形是否是正方形?并说明理由.
① 对角线互相垂直且相等的平行四边形.
② 对角线互相垂直的矩形.
③ 对角线相等的菱形.
④ 对角线互相垂直平分且相等的四边形.① 有一个角是直角的菱形是正方形.
② 有一组邻边相等的矩形是正方形.
③ 对角线相等的菱形是正方形.
④ 对角线互相垂直的矩形是正方形.
对角线互相垂直平分且相等的四
边形是正方形.正方形的判定方法: 例8.已知:正方形ABCD中,点A1、B1、C1、D1分别在AB 、BC 、CD 、DA上,且AA1=BB1=CC1=DD1,试判断四边形A1B1C1D1是正方形吗?为什么?证明四个三角形全等证明四边形A1B1C1D1为菱形证明四边形A1B1C1D1为正方形分
析小 结: 课堂小结:一、正方形的性质1. 正方形是特殊的平行四边形,具备平行
四边形的所有性质.
2. 正方形是特殊的矩形和菱形,具备它们
的所有特征.3. 正方形的四条边都相等.4. 正方形的两条对角线互相垂直平分且相
等,并且分别平分每一组对角.5. 正方形即是轴对称图形.二、正方形的判定
