人教版九年级下册26.1.2反比例函数的图象和性质课件(共29张PPT)
文档属性
| 名称 | 人教版九年级下册26.1.2反比例函数的图象和性质课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 14:49:47 | ||
图片预览







文档简介
(共29张PPT)
课程:数学
《反比例函数的图象和性质》
人教版
九年级下册 第2课时
第 26 章 反比例函数
教学目标
探索并掌握反比例函数的主要性质,逐步提高从函数图象获取信息的能力,体会数形结合的思想。
知识与技能
通过观察图象,概括反比例函数的有关性质,训练学生的概括、总结能力。
过程与方法
让学生积极参与到数学学习活动中,增强他们对数学学习的好奇心与求知欲。
情感态度和价值观
目
录
新课导入
New class introduction
探究新知
Explore new knowledge
课堂练习
class exercise
课堂小结
Class summary
01
02
03
04
新课导入
01
New class introduction
新课导入
1.什么是反比例函数?
2.反比例函数的定义中需要注意什么?
(1)k 是非零常数.
(2)xy = k.
一般地,形如 y = ( k是常数, k ≠0 )
的函数叫做反比例函数.
k
x
—
新课导入
3.还记得一次函数的图像与性质吗?
4、还记得二次函数的图像与性质吗?
5、如何画函数的图像?
提问:反比例函数的图像与性质又如何呢?
这节课开始我们来一起探究吧。
函数图象画法
描点法
列
表
描
点
连
线
探究新知
02
Explore new knowledge
探究新知
x
画出反比例函数 和
的函数图象.
y =
x
6
y =
x
6
函数图象画法
y =
x
6
y =
x
6
描点法
列
表
描
点
连
线
探究新知
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
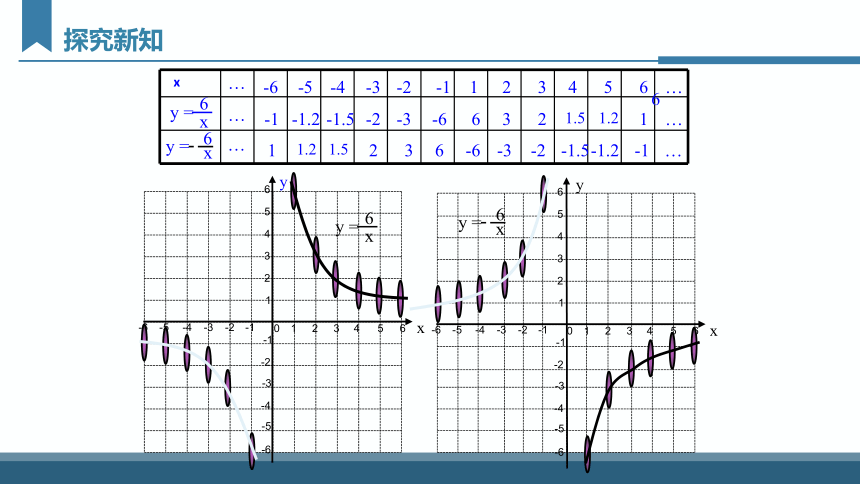
x
y
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y =
x
6
y =
x
6
探究新知
你认为作反比例函数图象时应注意哪些问题?
1.列表时,选取的自变量的值,既要易于计算,又要便于描点,尽量多取一些数值(取互为相反数的一对一对的数),多描一些点,这样既可以方便连线,又可以使图象精确.
2.描点时要严格按照表中所列的对应值描点,绝对不能把点的位置描错.
3.线连时一定要养成按自变量从小到大的顺序依次画线,连线时必须用光滑的曲线连接各点,不能用折线连接.
4.图象是延伸的,注意不要画的有明确端点.
5.曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.
探究新知
1
2
3
4
5
6
-4
-1
-2
.
-3
-5
-6
1
2
4
5
6
3
-6
-5
-1
-3
-4
-2
0
.
.
.
.
.
y
x
.
.
.
.
y=—
4
x
.
x
y
0
1
3
2
4
5
6
1
2
3
4
5
6
-6
-6
-5
-3
-4
-1
-2
-4
-5
-3
-2
-1
.
.
.
.
.
.
.
.
y = —
-4
x
.
探究新知
位置:
函数 的两支曲线分别位于第一、三象限内.
函数 的两支曲线分别位于第二、四象限内.
形状:
反比例函数的图象是由两支曲线组成的.
因此称反比例函数的图象为双曲线.
【结论】
探究新知
反比例函数 的图象在哪两个象限,由什么确定?
当k>0时,两支曲线分别位于第一,三象限内;
当k<0时,两支曲线分别位于第二,四象限内.
答:由k的符号决定.
探究新知
K>0
K<0
当k>0时,函数图象
的两个分支分别在第
一、三象限,在每个
象限内,y随x的增大
而减小.
当k<0时,函数图象
的两个分支分别在第
二、四象限,在每个
象限内,y随x的增大
而增大.
1.反比例函数的图象是双曲线;
2.图象性质见下表:
图
象
性质
y=
归纳:反比例函数的图象和性质:
探究新知
P(m,n)
A
o
y
x
P(m,n)
A
o
y
x
面积性质一
探究新知
P(m,n)
A
o
y
x
B
P(m,n)
A
o
y
x
B
面积性质二
探究新知
P(m,n)
A
o
y
x
P/
面积性质三
课堂练习
03
class exercise
课堂练习
A.
x
y
o
B.
x
y
o
D.
x
y
o
C.
x
y
o
1.反比例函数y= - 的图象大致是( )
D
课堂练习
图象大致是(
)
B
课堂练习
3.若函数 y=
m+2
x
的图象在其象限内 y 的值随 x 值的增大
B
而增大,则 m 的取值范围是(
A.m>-2
C.m>2
)
B.m<-2
D.m<2
解析:反比例函数在其象限内 y 的值随 x 值的增大而增大,
则需要 m+2<0,所以 m<-2.
课堂练习
的图象交于点 M(a,1),MN⊥x 轴于点N(如图 26-1-6),若△OMN
的面积等于 2,求这两个函数的解析式.
图 26-1-6
课堂练习
课堂练习
5.函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .
-1
-1-20
课堂练习
如图,已知一次函数y=kx+b(k≠0)的图象与x轴.y轴分别交于A.B两点,且与反比例函数 y=m/x(m≠0)的图象在第一象限内交于C点,CD垂直于x轴,垂足为点D,若OA=OB=OD=1.
(1)求点A.B.D的坐标;
(2)求一次函数和
反比例函数的解析式
D
B
A
C
y
x
O
课堂练习
B
A
C
y
x
O
解(1)A(-1,0)B(1,0)
C(1,0)
(2)把A(-1,1)B(1,0)代入y=kx+b中得 b=1 -k+b=0 ∴k=1 ∴y=x+1
当x=1时,y=1+1=2 ∴C(1,2)
把C(1,2)代入y=m/x中 2=m/1
∴m=2 ∴y=2/x
课堂小结
04
Class summary
课堂小结
探究:y= (k≠0)可变形为 k=__________.
1.反比例函数的图象
xy
(1)当 k>0 时,由于______得正,因此可以判断 x,y 的符号________,所以点(x,y)在____________象限,所以函数图象位
于__________象限.
相同
第一或第三
一、三
xy
(2)当 k<0 时,由于__________得负,因此可以判断 x,y的符号________,所以点(x,y)在____________象限,所以函数
图象位于__________象限.
二、四
归纳:反比例函数的图象是_______,它有_____分支.
两个
当 k>0 时,函数图象位于____________象限;
当 k<0 时,函数图象位于____________象限.
xy
相反
第二或第四
双曲线
一、三
二、四
课堂小结
2.反比例函数的性质
(1)形状:________线.
双曲
(2)位置:k>0 时,图象在第________象限;
一、三
k<0 时,图象在第________象限.
二、四
(3)增减性:
k>0 时,在每一个象限内,y 随 x 的增大而______;
k<0 时,在每一个象限内,y 随 x 的增大而______.
减小
增大
课程:数学
《反比例函数的图象和性质》
人教版
九年级下册 第2课时
第 26 章 反比例函数
教学目标
探索并掌握反比例函数的主要性质,逐步提高从函数图象获取信息的能力,体会数形结合的思想。
知识与技能
通过观察图象,概括反比例函数的有关性质,训练学生的概括、总结能力。
过程与方法
让学生积极参与到数学学习活动中,增强他们对数学学习的好奇心与求知欲。
情感态度和价值观
目
录
新课导入
New class introduction
探究新知
Explore new knowledge
课堂练习
class exercise
课堂小结
Class summary
01
02
03
04
新课导入
01
New class introduction
新课导入
1.什么是反比例函数?
2.反比例函数的定义中需要注意什么?
(1)k 是非零常数.
(2)xy = k.
一般地,形如 y = ( k是常数, k ≠0 )
的函数叫做反比例函数.
k
x
—
新课导入
3.还记得一次函数的图像与性质吗?
4、还记得二次函数的图像与性质吗?
5、如何画函数的图像?
提问:反比例函数的图像与性质又如何呢?
这节课开始我们来一起探究吧。
函数图象画法
描点法
列
表
描
点
连
线
探究新知
02
Explore new knowledge
探究新知
x
画出反比例函数 和
的函数图象.
y =
x
6
y =
x
6
函数图象画法
y =
x
6
y =
x
6
描点法
列
表
描
点
连
线
探究新知
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y =
x
6
y =
x
6
探究新知
你认为作反比例函数图象时应注意哪些问题?
1.列表时,选取的自变量的值,既要易于计算,又要便于描点,尽量多取一些数值(取互为相反数的一对一对的数),多描一些点,这样既可以方便连线,又可以使图象精确.
2.描点时要严格按照表中所列的对应值描点,绝对不能把点的位置描错.
3.线连时一定要养成按自变量从小到大的顺序依次画线,连线时必须用光滑的曲线连接各点,不能用折线连接.
4.图象是延伸的,注意不要画的有明确端点.
5.曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.
探究新知
1
2
3
4
5
6
-4
-1
-2
.
-3
-5
-6
1
2
4
5
6
3
-6
-5
-1
-3
-4
-2
0
.
.
.
.
.
y
x
.
.
.
.
y=—
4
x
.
x
y
0
1
3
2
4
5
6
1
2
3
4
5
6
-6
-6
-5
-3
-4
-1
-2
-4
-5
-3
-2
-1
.
.
.
.
.
.
.
.
y = —
-4
x
.
探究新知
位置:
函数 的两支曲线分别位于第一、三象限内.
函数 的两支曲线分别位于第二、四象限内.
形状:
反比例函数的图象是由两支曲线组成的.
因此称反比例函数的图象为双曲线.
【结论】
探究新知
反比例函数 的图象在哪两个象限,由什么确定?
当k>0时,两支曲线分别位于第一,三象限内;
当k<0时,两支曲线分别位于第二,四象限内.
答:由k的符号决定.
探究新知
K>0
K<0
当k>0时,函数图象
的两个分支分别在第
一、三象限,在每个
象限内,y随x的增大
而减小.
当k<0时,函数图象
的两个分支分别在第
二、四象限,在每个
象限内,y随x的增大
而增大.
1.反比例函数的图象是双曲线;
2.图象性质见下表:
图
象
性质
y=
归纳:反比例函数的图象和性质:
探究新知
P(m,n)
A
o
y
x
P(m,n)
A
o
y
x
面积性质一
探究新知
P(m,n)
A
o
y
x
B
P(m,n)
A
o
y
x
B
面积性质二
探究新知
P(m,n)
A
o
y
x
P/
面积性质三
课堂练习
03
class exercise
课堂练习
A.
x
y
o
B.
x
y
o
D.
x
y
o
C.
x
y
o
1.反比例函数y= - 的图象大致是( )
D
课堂练习
图象大致是(
)
B
课堂练习
3.若函数 y=
m+2
x
的图象在其象限内 y 的值随 x 值的增大
B
而增大,则 m 的取值范围是(
A.m>-2
C.m>2
)
B.m<-2
D.m<2
解析:反比例函数在其象限内 y 的值随 x 值的增大而增大,
则需要 m+2<0,所以 m<-2.
课堂练习
的图象交于点 M(a,1),MN⊥x 轴于点N(如图 26-1-6),若△OMN
的面积等于 2,求这两个函数的解析式.
图 26-1-6
课堂练习
课堂练习
5.函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .
-1
-1
课堂练习
如图,已知一次函数y=kx+b(k≠0)的图象与x轴.y轴分别交于A.B两点,且与反比例函数 y=m/x(m≠0)的图象在第一象限内交于C点,CD垂直于x轴,垂足为点D,若OA=OB=OD=1.
(1)求点A.B.D的坐标;
(2)求一次函数和
反比例函数的解析式
D
B
A
C
y
x
O
课堂练习
B
A
C
y
x
O
解(1)A(-1,0)B(1,0)
C(1,0)
(2)把A(-1,1)B(1,0)代入y=kx+b中得 b=1 -k+b=0 ∴k=1 ∴y=x+1
当x=1时,y=1+1=2 ∴C(1,2)
把C(1,2)代入y=m/x中 2=m/1
∴m=2 ∴y=2/x
课堂小结
04
Class summary
课堂小结
探究:y= (k≠0)可变形为 k=__________.
1.反比例函数的图象
xy
(1)当 k>0 时,由于______得正,因此可以判断 x,y 的符号________,所以点(x,y)在____________象限,所以函数图象位
于__________象限.
相同
第一或第三
一、三
xy
(2)当 k<0 时,由于__________得负,因此可以判断 x,y的符号________,所以点(x,y)在____________象限,所以函数
图象位于__________象限.
二、四
归纳:反比例函数的图象是_______,它有_____分支.
两个
当 k>0 时,函数图象位于____________象限;
当 k<0 时,函数图象位于____________象限.
xy
相反
第二或第四
双曲线
一、三
二、四
课堂小结
2.反比例函数的性质
(1)形状:________线.
双曲
(2)位置:k>0 时,图象在第________象限;
一、三
k<0 时,图象在第________象限.
二、四
(3)增减性:
k>0 时,在每一个象限内,y 随 x 的增大而______;
k<0 时,在每一个象限内,y 随 x 的增大而______.
减小
增大
