人教版九年级下册26.1.1反比例函数课件(共23张PPT)
文档属性
| 名称 | 人教版九年级下册26.1.1反比例函数课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
课程:数学
《反比例函数》
人教版
九年级下册 第1课时
第 26 章 反比例函数
教学目标
理解反比例函数的概念,能判断两个变量之间的关系是否是函数关系,进而识别反比例函数并能根据已知条件确定反比例函数的表达式。
知识与技能
体会数学从实践中来又到实际中去的研究、应用过程培养学生的观察能力,及数学地发现问题,解决问题的能力。
过程与方法
在学生探索过程中,让学生体会到在探索的途径和方法上与一次函数相似,让学生感受到亲切自然,激发学生的学习兴趣,提高学生思考问题的积极主动性从而培养对数学学科的浓厚兴趣。
情感态度和价值观
目
录
新课导入
New class introduction
探究新知
Explore new knowledge
课堂练习
class exercise
课堂小结
Class summary
01
02
03
04
新课导入
01
New class introduction
新课导入
1、什么是函数?我们学习了几种函数?
2、什么是正比例函数?
3、什么是一次函数?
4、什么是二次函数?
5、在一次函数、二次函数中自变量的取值
范围分别是什么?
探究新知
02
Explore new knowledge
探究新知
物理与数学
欧姆定律
我们知道,电流I,电阻R,电压U之间满足关系式U=IR.当U=220V时.
(1)你能用含有R的代数式表示I吗
(2)利用写出的关系式完成下表:
当R越来越大时,I怎样变化 当R越来越小呢
(3)变量I是R的函数吗 为什么
R/Ω 20 40 60 80 100
I/A
11 5.5 3.67 2.75 2.2
探究新知
运动中的数学
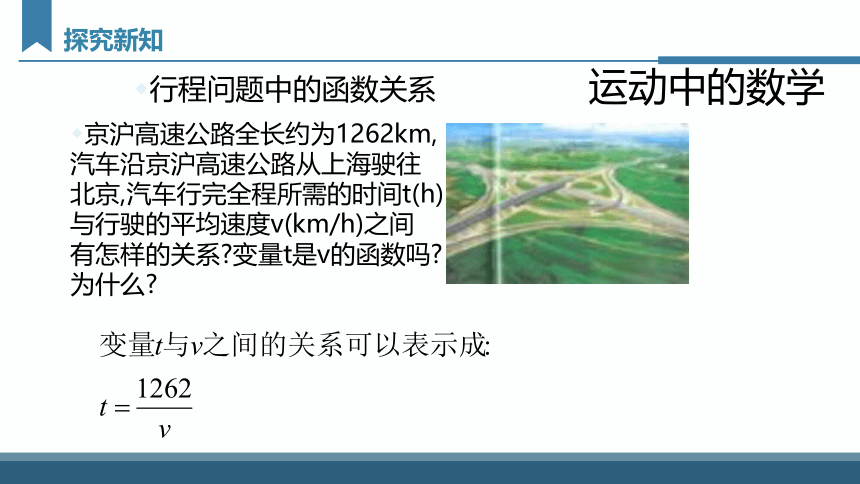
行程问题中的函数关系
京沪高速公路全长约为1262km,汽车沿京沪高速公路从上海驶往北京,汽车行完全程所需的时间t(h)与行驶的平均速度v(km/h)之间 有怎样的关系 变量t是v的函数吗 为什么
探究新知
某机械厂加工一批零件,每小时加工的数量和所需的加工时间如下表:
工程中的数学
探究新知
1.由上面的问题中我们得到这样的三个函数,你能指出自变量和函数吗
2.上面的函数关系式形式上有什么的共同点
k
都是 的形式,其中k是常数.
y=
x
3.反比例函数的定义
一般地,形如 (k是常数,k≠0)的函数称为反比例函数,其中x是自变量,y是函数.
y=
k
x
4.反比例函数的自变量的取值范围是
不为0的全体实数
有时反比例函数也写成y=kx-1或xy=k的形式.
“行家”看门道
探究新知
y =
3
2x
y =
x
1
y =
1
3x
y = 3x-1
y = 2x
下列函数中哪些是反比例函数 并说出它的k。哪些是一次函数
反比例函数
一次函数
探究新知
⑵ 在下列函数中,y是x的反比例函数的是( )
(A) (B)
(C)xy = 5 (D)
⑶ 已知函数 是正比例函数,则 m = ___ ;
已知函数 是反比例函数,则 m = ___ 。
y =
8
X+5
y =
x
3
y =
x2
2x
y = xm -7
y = 3xm -7
C
8
6
【现场提问】
已知函数 是反比例函数,则 m = ___ 。
y = (m-3)x2-|m|
-3
判断一个等式为反比例函数,要两个条件:
(1)自变量的指数为-1;
(2)自变量系数不为0.
探究新知
【待定系数法求反比例函数的表达式】
【例 2】 (1)已知变量 y 与 x 成反比例,并且当 x=3 时,y=7,①写出 y 与 x 之间的函数解析式;②求当 x=7 时函数的值;
(2)已知函数 y=y1-y2,y1 与 x 成正比例,y2 与(x-2)成反比例,且当 x=3 时,y=5;当 x=1 时,y=-1,求出 y 与 x的函数解析式.
(2)y2与(x-2)成反比例中,学会把(x-2)看作一个整体.
探究新知
课堂练习
03
class exercise
课堂练习
1.下列函数中,是反比例函数的是(
)
D
2.已知函数 y=kxk-2 是反比例函数,求 k 的值.
解:由题意得,k-2=-1 且 k≠0,解得 k=1.
课堂练习
为__________.
2
4.如图 26-1-1,某反比例函数的图象过点(-2,1),
则此反
)
B
比例函数的解析式为(
课堂练习
5 .近视眼镜的度数y(度)与镜片焦距x(米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数y与镜片焦距x之间的函数关系式是___________。
6.反比例函数 中,当x的值由4增加到6时,y的值减小3,求这个反比例函数的解析式.
课堂练习
7.当m= 时,关于x的函数
y=(m+1)xm2-2是反比例函数?
分析:
{
m2-2=-1
m+1≠0
{
即
m=±1
m≠-1
1
课堂练习
解:由题意知
由 x=1 时,y=4
课堂练习
课堂小结
04
Class summary
课堂小结
1.反比例函数的定义
(1)形如_____________________的函数,叫做反比例函数,
其中 x 是________,y 是函数.
自变量
(2)自变量 x 的取值范围是_________的一切实数.
2.“待定系数法”确定函数解析式
若 y 是 x 的一次函数,则设 y=___________________;
若 y 是 x 的正比例函数,则设 y=_________________;
若 y 是 x 的反比例函数,则设 y=_________________.
不等于 0
kx+b(k为常数,k≠0)
kx(k为常数,k≠0)
课程:数学
《反比例函数》
人教版
九年级下册 第1课时
第 26 章 反比例函数
教学目标
理解反比例函数的概念,能判断两个变量之间的关系是否是函数关系,进而识别反比例函数并能根据已知条件确定反比例函数的表达式。
知识与技能
体会数学从实践中来又到实际中去的研究、应用过程培养学生的观察能力,及数学地发现问题,解决问题的能力。
过程与方法
在学生探索过程中,让学生体会到在探索的途径和方法上与一次函数相似,让学生感受到亲切自然,激发学生的学习兴趣,提高学生思考问题的积极主动性从而培养对数学学科的浓厚兴趣。
情感态度和价值观
目
录
新课导入
New class introduction
探究新知
Explore new knowledge
课堂练习
class exercise
课堂小结
Class summary
01
02
03
04
新课导入
01
New class introduction
新课导入
1、什么是函数?我们学习了几种函数?
2、什么是正比例函数?
3、什么是一次函数?
4、什么是二次函数?
5、在一次函数、二次函数中自变量的取值
范围分别是什么?
探究新知
02
Explore new knowledge
探究新知
物理与数学
欧姆定律
我们知道,电流I,电阻R,电压U之间满足关系式U=IR.当U=220V时.
(1)你能用含有R的代数式表示I吗
(2)利用写出的关系式完成下表:
当R越来越大时,I怎样变化 当R越来越小呢
(3)变量I是R的函数吗 为什么
R/Ω 20 40 60 80 100
I/A
11 5.5 3.67 2.75 2.2
探究新知
运动中的数学
行程问题中的函数关系
京沪高速公路全长约为1262km,汽车沿京沪高速公路从上海驶往北京,汽车行完全程所需的时间t(h)与行驶的平均速度v(km/h)之间 有怎样的关系 变量t是v的函数吗 为什么
探究新知
某机械厂加工一批零件,每小时加工的数量和所需的加工时间如下表:
工程中的数学
探究新知
1.由上面的问题中我们得到这样的三个函数,你能指出自变量和函数吗
2.上面的函数关系式形式上有什么的共同点
k
都是 的形式,其中k是常数.
y=
x
3.反比例函数的定义
一般地,形如 (k是常数,k≠0)的函数称为反比例函数,其中x是自变量,y是函数.
y=
k
x
4.反比例函数的自变量的取值范围是
不为0的全体实数
有时反比例函数也写成y=kx-1或xy=k的形式.
“行家”看门道
探究新知
y =
3
2x
y =
x
1
y =
1
3x
y = 3x-1
y = 2x
下列函数中哪些是反比例函数 并说出它的k。哪些是一次函数
反比例函数
一次函数
探究新知
⑵ 在下列函数中,y是x的反比例函数的是( )
(A) (B)
(C)xy = 5 (D)
⑶ 已知函数 是正比例函数,则 m = ___ ;
已知函数 是反比例函数,则 m = ___ 。
y =
8
X+5
y =
x
3
y =
x2
2x
y = xm -7
y = 3xm -7
C
8
6
【现场提问】
已知函数 是反比例函数,则 m = ___ 。
y = (m-3)x2-|m|
-3
判断一个等式为反比例函数,要两个条件:
(1)自变量的指数为-1;
(2)自变量系数不为0.
探究新知
【待定系数法求反比例函数的表达式】
【例 2】 (1)已知变量 y 与 x 成反比例,并且当 x=3 时,y=7,①写出 y 与 x 之间的函数解析式;②求当 x=7 时函数的值;
(2)已知函数 y=y1-y2,y1 与 x 成正比例,y2 与(x-2)成反比例,且当 x=3 时,y=5;当 x=1 时,y=-1,求出 y 与 x的函数解析式.
(2)y2与(x-2)成反比例中,学会把(x-2)看作一个整体.
探究新知
课堂练习
03
class exercise
课堂练习
1.下列函数中,是反比例函数的是(
)
D
2.已知函数 y=kxk-2 是反比例函数,求 k 的值.
解:由题意得,k-2=-1 且 k≠0,解得 k=1.
课堂练习
为__________.
2
4.如图 26-1-1,某反比例函数的图象过点(-2,1),
则此反
)
B
比例函数的解析式为(
课堂练习
5 .近视眼镜的度数y(度)与镜片焦距x(米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数y与镜片焦距x之间的函数关系式是___________。
6.反比例函数 中,当x的值由4增加到6时,y的值减小3,求这个反比例函数的解析式.
课堂练习
7.当m= 时,关于x的函数
y=(m+1)xm2-2是反比例函数?
分析:
{
m2-2=-1
m+1≠0
{
即
m=±1
m≠-1
1
课堂练习
解:由题意知
由 x=1 时,y=4
课堂练习
课堂小结
04
Class summary
课堂小结
1.反比例函数的定义
(1)形如_____________________的函数,叫做反比例函数,
其中 x 是________,y 是函数.
自变量
(2)自变量 x 的取值范围是_________的一切实数.
2.“待定系数法”确定函数解析式
若 y 是 x 的一次函数,则设 y=___________________;
若 y 是 x 的正比例函数,则设 y=_________________;
若 y 是 x 的反比例函数,则设 y=_________________.
不等于 0
kx+b(k为常数,k≠0)
kx(k为常数,k≠0)
