第22章 相似形单元测试卷(标准难度)(含答案)
文档属性
| 名称 | 第22章 相似形单元测试卷(标准难度)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 339.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 15:38:10 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
沪科版初中数学九年级上册第22章《相似形》单元测试卷
考试范围:第22章;考试时间:120分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共12小题,共36分)
如图,在平行四边形中,点是上的点,,直线交于点,交的延长线于点,则的值为( )
A. B. C. D.
如图,已知.
以点为圆心,以适当长为半径画弧,交于点,交于点.
分别以,为圆心,以大于的长为半径画弧,两弧在的内部相交于点.
作射线交于点.
分别以,为圆心,以大于的长为半径画弧,两弧相交于,两点.
作直线,交,分别于点,.
依据以上作图,若,,,则的长是( )
A. B. C. D.
如图,,,,,,若在边上有点,使与相似,则这样的点有( )
A. 个 B. 个 C. 个 D. 个
如图,在中,点在上一点,下列条件中,能使与相似的是( )
A. B.
C. D.
如图,在 中,延长至点,使,连接交于点,交于点,则的值是( )
A. B. C. D.
如图,在中,,,四边形的面积为,则的面积是( )
A.
B.
C.
D.
将一张以为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形剪掉的两个直角三角形相似,剩下的是如图所示的四边形纸片,其中,,,,,则剪掉的两个直角三角形的斜边长不可能是( )
A. B. C. D.
如图,平面直角坐标系中,点,的坐标分别为、,是关于点的位似图形,且的坐标为,则点的坐标为( )
B.
D.
西游记的故事家喻户晓,特别是书中的孙悟空嫉恶如仇斩妖除魔大快人心在一次降妖过程中,孙悟空念动咒语将一片树叶放大后射向妖魔假如这个过程可以看成是在平面直角坐标系中的一次无旋转的变换,设变化前树叶尖部点坐标为,在咒语中变化后得到对应点为则变化后树叶的面积变为原来的( )
A. 倍 B. 倍 C. 倍 D. 倍
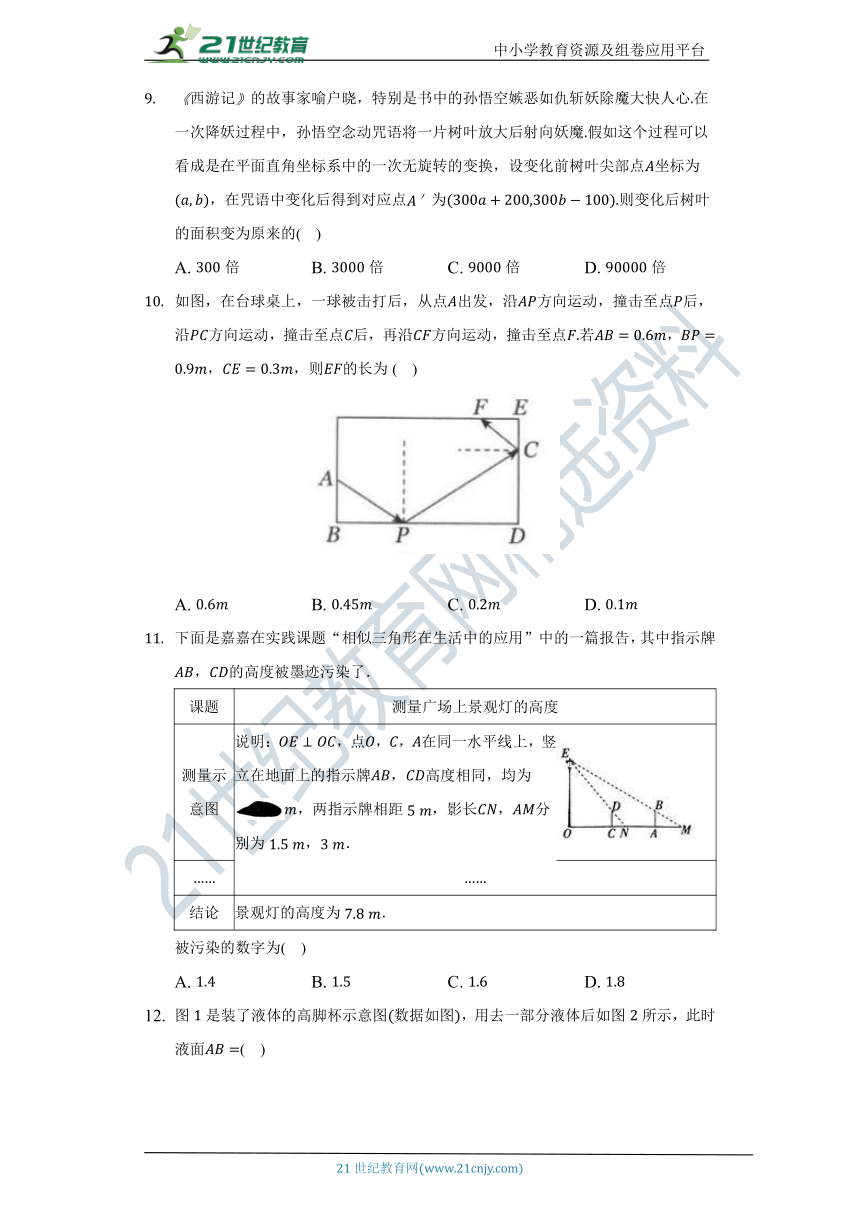
如图,在台球桌上,一球被击打后,从点出发,沿方向运动,撞击至点后,沿方向运动,撞击至点后,再沿方向运动,撞击至点若,,,则的长为( )
A. B. C. D.
下面是嘉嘉在实践课题“相似三角形在生活中的应用”中的一篇报告,其中指示牌,的高度被墨迹污染了.
课题 测量广场上景观灯的高度
测量示意图 说明:,点,,在同一水平线上,竖立在地面上的指示牌,高度相同,均为,两指示牌相距,影长,分别为,.
结论 景观灯的高度为.
被污染的数字为( )
A. B. C. D.
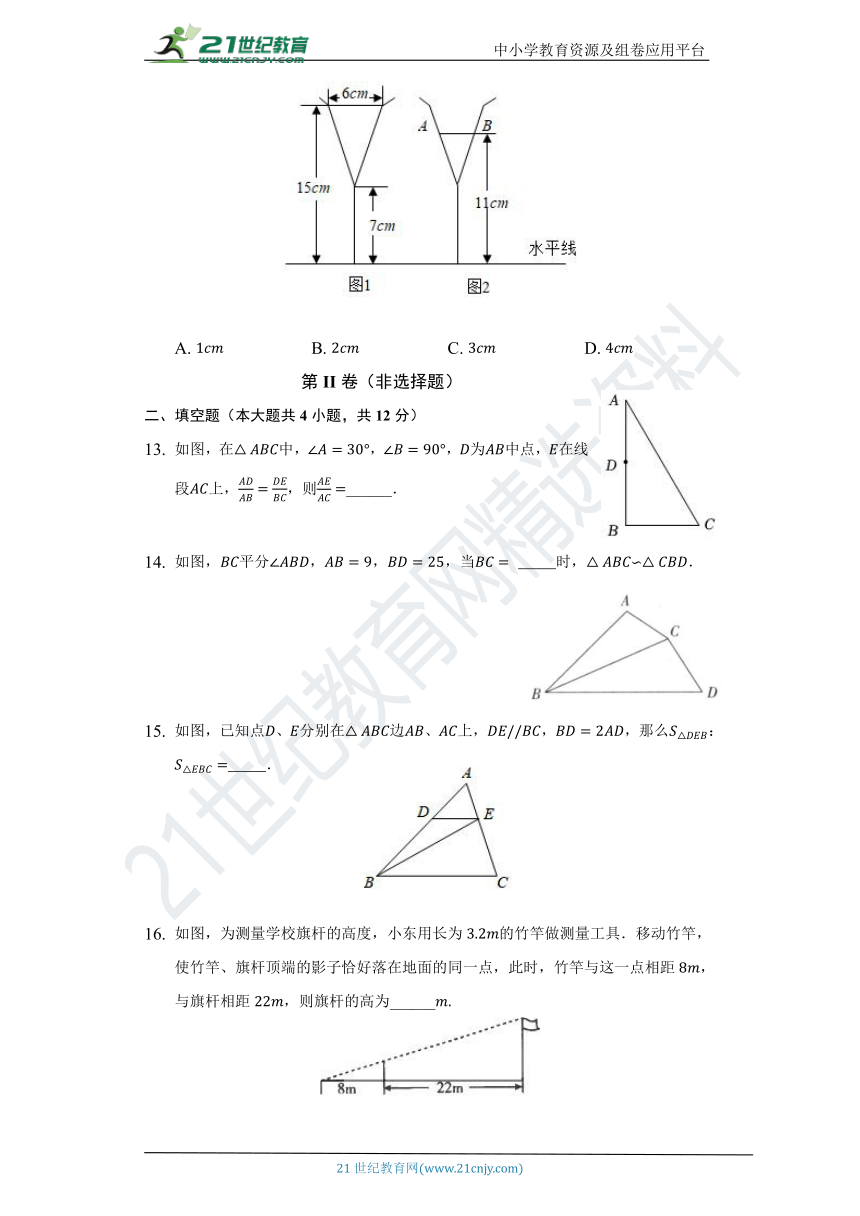
图是装了液体的高脚杯示意图数据如图,用去一部分液体后如图所示,此时液面( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
如图,在中,,,为中点,在线段上,,则______.
如图,平分,,,当 时,∽.
如图,已知点、分别在边、上,,,那么: .
如图,为测量学校旗杆的高度,小东用长为的竹竿做测量工具.移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距,与旗杆相距,则旗杆的高为______
三、解答题(本大题共9小题,共72.分)
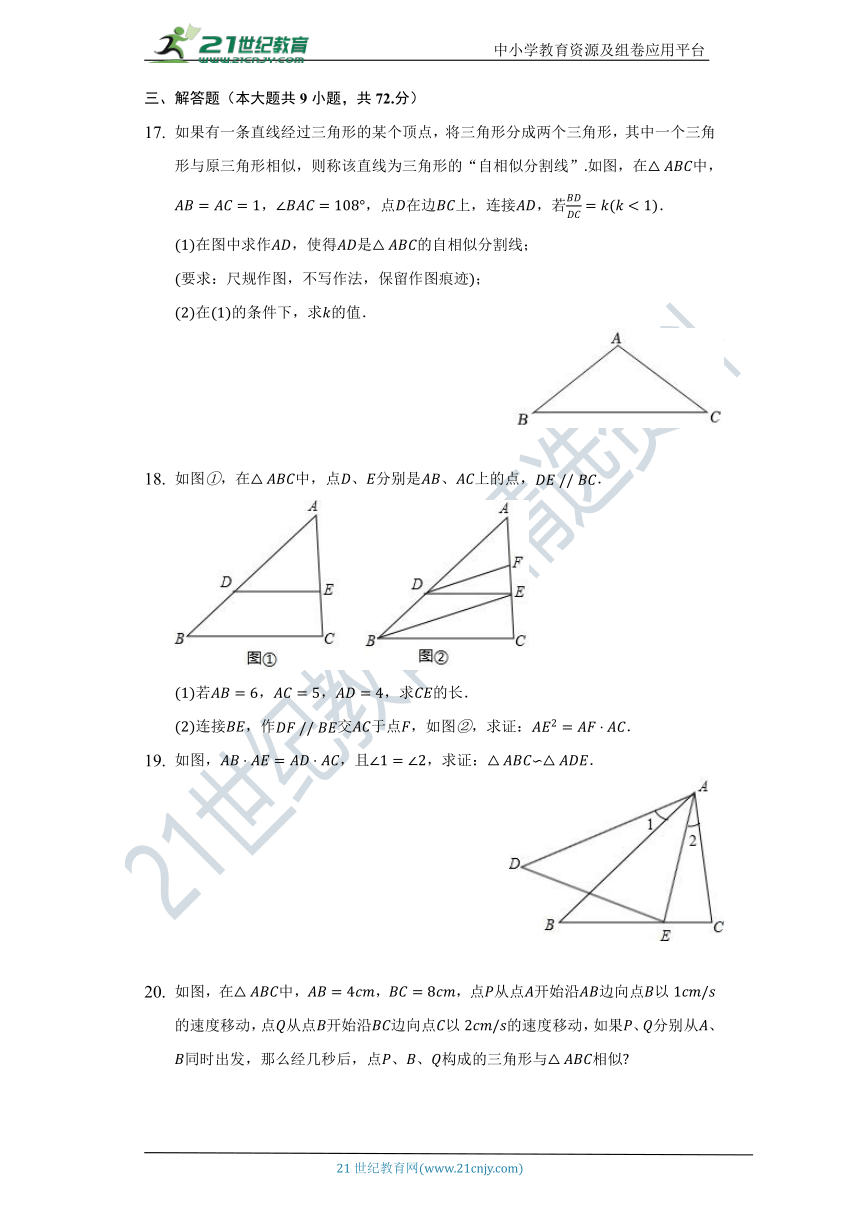
如果有一条直线经过三角形的某个顶点,将三角形分成两个三角形,其中一个三角形与原三角形相似,则称该直线为三角形的“自相似分割线”如图,在中,,,点在边上,连接,若.
在图中求作,使得是的自相似分割线;
要求:尺规作图,不写作法,保留作图痕迹;
在的条件下,求的值.
如图,在中,点、分别是、上的点,.
若,,,求的长.
连接,作交于点,如图,求证:.
如图,,且,求证:∽.
如图,在中,,,点从点开始沿边向点以的速度移动,点从点开始沿边向点以的速度移动,如果、分别从、同时出发,那么经几秒后,点、、构成的三角形与相似
如图,在与中,点、分别在边、上,且∽,若______,则∽.
请从;;这个选项中选择一个作为条件写序号,并加以证明.
如图,已知.
尺规作图:作平行四边形;保留作图痕迹,不写作法
在所作的平行四边形中,连接,交于点.
若,,,求的长;
过点作直线与边,分别交于点,,设四边形的面积为
,平行四边形的面积为,求:的值.
如图,在平面直角坐标系中,把以格点为顶点的三角形称为格点三角形每个小方格都是边长为的正方形图中是格点三角形,点、、的坐标分别是,,.
画出关于轴对称的;
以为位似中心,在第一象限内将放大为原来的倍,得到,画出;
内有一点,直接写出经过位似变换后的对应点的坐标________________.
阳光明媚的一天实践课上,亮亮准备用所学知识测量教学楼前一座假山的高度,如图,亮亮在地面上的点处,眼睛贴地观察,看到假山顶端、教学楼顶端在一条直线上.此时他起身在处站直,发现自己的影子末端和教学楼的影子末端恰好重合于点处,测得米,亮亮的身高为米.假山的底部处因有花园围栏,无法到达,但经询问和进行部分测量后得知,米,点、、、在一条直线上,,,,已知教学楼的高度为米,请你求出假山的高度.
如图,在相对的两栋楼中间有一堵墙,甲、乙两人分别在这两栋楼内观察这堵墙,视线如图所示根据实际情况画出平面图形如图,甲从点可以看到点处,乙从点可以看到点处,是的中点,墙高,,,求甲、乙两人的观测点到地面的距离之差.
答案和解析
1.【答案】
【解析】解:由,可以假设,则,,
四边形是平行四边形,
,,,
,
故选:.
由,可以假设,则,,证明,,再利用平行线分线段成比例定理即可解决问题.
本题考查平行四边形的性质,解题的关键是学会利用参数解决问题,属于中考常考题型.
2.【答案】
【解析】解:由作法得平分,垂直平分,
,,,
,
,
,
,
同理可得,
四边形为平行四边形,
而,
四边形为菱形,
,
,
,即,
.
故选:.
利用作法得平分,垂直平分,所以,,,再证明四边形为菱形得到,然后利用平行线分线段成比例定理计算的长.
本题考查了作图复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了角平分线的性质和垂直平分线的性质.
3.【答案】
【解析】解:.,
,
.
设的长为,则长为.
若边上存在点,使与相似,那么分两种情况:
若∽,则::,
即::,
解得:
若∽,则::,
即::,
整理得:,
,
这种情形不存在,
满足条件的点的个数是个,
故选:.
根据已知分两种情况∽或∽来进行分析,求得的长,从而确定存在的个数.
此题考查了相似三角形的判定,依据相似三角形的判定定理列出关于的方程是解题的关键.
4.【答案】
【解析】解:选项A、、的条件无法判断与相似.
正确答案是D理由如下:
,
,
,
∽两边成比例夹角相等的两个三角形相似.
故选:.
根据两边成比例夹角相等的两个三角形相似,即可判断.
本题考查相似三角形的判定和性质,解题的关键是灵活运用所学知识解决问题,属于基础题,中考常考题型.
5.【答案】
【解析】解:四边形是平行四边形,
,,
∽,
,
,
,
,
,
,
,
∽,
,
故选:.
根据平行四边形的性质得出,利用相似三角形的判定和性质解答即可.
此题考查平行四边形的性质,关键是根据相似三角形的判定和性质解答.
6.【答案】
【解析】解:,
∽,
,
.
,即,
.
故选:.
由可得出∽,利用相似三角形的性质可得出,结合即可得出关于的一元一次方程,解之即可得出结论.
本题考查了相似三角形的判定与性质,利用相似三角形的性质,找出是解题的关键.
7.【答案】
【解析】解:如右图所示,
由已知可得,∽,
则,
设,,
则,
解得,
,故选项B不符合题意;
,故选项D不符合题意;
如图所示,
由已知可得,∽,
则,
设,,
则,
解得,
,故选项C不符合题意;
,
故选:.
根据题意,画出相应的图形,然后利用相似三角形的性质和分类讨论的方法,求出剪掉的两个直角三角形的斜边长,然后即可判断哪个选项符合题意.
本题考查相似三角形的性质、矩形的性质,解答本题的关键是明确题意,利用分类讨论的方法解答.
8.【答案】
【解析】
【分析】
本题考查的是位似变换的概念和性质、相似三角形的性质,如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行或共线,那么这样的两个图形叫做位似图形.
过点作轴于点,作轴于点,根据位似变换的性质得到,根据相似三角形的性质列出比例式,计算即可.
【解答】
解:过点作轴于点,过作轴于点,
则,
由题意得,,,
点、的坐标分别为、,是关于的的位似图形,且的坐标为,
,
,
,
∽,
,即,
解得,,,
,
则点的坐标为,
故选:.
9.【答案】
【解析】
【分析】
树叶端点变为,可拆分为两次变换所得,第一次是位似变换,第二次是平移变换.平移变换可决定树叶最终的位置,而面积只与位似变换有关,所以只需考虑位似变换即可得答案.
本题主要考查几何变换类型,解题的关键是根据对应点的坐标判断出其几何变换类型.
【解答】
解:由点经过变换后得到的对应点为为知,
此树叶所作的变换是位似变换和平移变换,变换的位似比为:,
则原树叶的面积与变换后的树叶的面积比为:,
故选D.
10.【答案】
【解析】
【分析】
本题主要考查相似三角形的应用,根据题意求出∽,由即可求出的长度.
【解答】
解:由题意知,
,
,
,
,
,
∽,
,
即,
,
11.【答案】
【解析】
【分析】
本题主要考查的是相似三角形的应用的有关知识,由题意可知,,利用相似三角形的判定和性质得到,,根据得到,设,进而得到,求出,进而求出即可.
【解答】
解:由题意可知,,
∽,∽,
,,
,
,
设,则,
,
.
.
12.【答案】
【解析】解:如图:过作,垂足为,过作,垂足为,
,
∽,即相似比为,
,
,,
,
,
故选:.
高脚杯前后的两个三角形相似.根据相似三角形的判定和性质即可得出结果.
本题考查相似三角形的应用,解本题的关键熟练掌握相似三角形的判定与性质.
13.【答案】
【解析】解:为中点,
.
当时,.
故答案是:.
利用平行线截线段成比例解答.
本题主要考查了平行线分线段成比例,平行于三角形的一边,并且和其他两边或两边的延长线相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.
14.【答案】
【解析】 平分,
,
当时,∽ ,
,舍,.
15.【答案】
【解析】解:,
::,
,
∽,
,
::.
和的高相同,设这个高为,
:,
故答案为:.
根据,求出:的值,再根据相似三角形的性质求得:,最后再根据面积之比即可求解.
本题主要考查了相似三角形的判定和性质,找准对应线段是解题的关键.
16.【答案】
【解析】解:因为,所以∽,
于是,即,解得:.
旗杆的高为.
易证∽,利用相似三角形的对应边成比例,列出方程求解即可.
本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程即可求出旗杆的高度.
17.【答案】解:如图,线段即为所求;
设.
,,
,
由作图可知,
,
,
,
,,
∽,
,
,
,
或,
经检验:是分式方程的解,且符合题意,
,
.
【解析】作线段的垂直平分线交于点,连接即可;
设利用相似三角形的性质构建方程求解即可.
本题考查作图相似变换,等腰三角形的性质,分式方程等知识,解题关键是理解题意,学会利用参数构建方程解决问题,属于中考常考题型.
18.【答案】解:如图,,
,即,
,
证明:如图,
,
,
,
,
,
.
【解析】本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.
如图,根据平行线分线段成比例定理得到,则利用比例性质可计算出的长,然后计算即可
由得到,由得到,利用等量代换得,然后利用比例的性质可得到结论.
19.【答案】证明:,
.
又,
,即,
∽.
【解析】由已知条件得到:,则由“两边及夹角法”证得结论.
本题考查了相似三角形的判定.
平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;
三边法:三组对应边的比相等的两个三角形相似;
两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;
两角法:有两组角对应相等的两个三角形相似.
20.【答案】解: 设经过后,,
根据已知条件,可得,.
,,,解得
设经过后,.
,,
,解得.
故经过或后,与相似.
【解析】本题考查了相似三角形的判定,利用分类思想解决问题是本题的关键分两种情况讨论,可得,或,可求的值.
21.【答案】
【解析】解:.
理由如下:∽,
,
,
,,,
,
∽.
利用相似三角形的判定:两角对应相等的两个三角形相似可证明.
本题主要考查相似三角形的判定,掌握相似三角形的判定条件是解题的关键.
22.【答案】解:如图所示,
即为所求;
如图,
四边形是平行四边形,,
,,
,,
,
;
如图,
四边形是平行四边形,
,,
,
≌,
,
,
四边形是平行四边形,
,,
,,
≌,
,
,
,
:.
【解析】分别以、为圆心,、为半径画弧,两弧交于点,连接、,即可得到平行四边形;
由平行四边形的性质得出,,由勾股定理得出,即可求出;
先证明≌,得出,即可得出,再证明≌,得出,得出,进而得出,即可得出:.
本题考查了作图复杂作图,平行四边形的判定与性质,勾股定理,熟练掌握平行四边形的判定与性质,基本作图,全等三角形的判定与性质,勾股定理等知识是解决问题的关键.
23.【答案】解:如图:即为所求
如图:即为所求
【解析】
【分析】
本题考查了作图位似变换:画位似图形的一般步骤为:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.也考查了轴对称变换.
利用网格特点和轴对称的性质画出点、、,从而得到;
根据位似图形的性质得出对应点坐标、、顺次连接即可;
根据点、、的坐标变化规律,进而得出旋转变换后的对应点的坐标.
【解答】
解:,见答案
点、、的坐标分别是、、,
点、、的坐标分别是、、,
内有一点,经过旋转变换后的对应点的坐标为;.
24.【答案】解:,,
,
∽,
,即,
解得.
,,
,
∽,
,即,
解得,
假山的高度为米.
【解析】依据∽,可得,进而得出米.再根据∽,可得,进而得出假山的高度为米.
本题主要考查了相似三角形的应用,测量不能到达顶部的物体的高度,通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.
25.【答案】解:由题意可知,
又是公共角,
∽,
,
,是的中点,
.
,,
.
又,为公共角
∽
,
.
.
甲、乙两人的观测点到地面的距离之差约为.
【解析】本题主要考查了相似三角形的应用,熟练掌握相似三角形的判定定理和性质定理是解决此题的关键.
首先证明∽,则可得,由是的中点,可得,则,由此即可求出的长,同理可求得的长,然后作差即可.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
沪科版初中数学九年级上册第22章《相似形》单元测试卷
考试范围:第22章;考试时间:120分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共12小题,共36分)
如图,在平行四边形中,点是上的点,,直线交于点,交的延长线于点,则的值为( )
A. B. C. D.
如图,已知.
以点为圆心,以适当长为半径画弧,交于点,交于点.
分别以,为圆心,以大于的长为半径画弧,两弧在的内部相交于点.
作射线交于点.
分别以,为圆心,以大于的长为半径画弧,两弧相交于,两点.
作直线,交,分别于点,.
依据以上作图,若,,,则的长是( )
A. B. C. D.
如图,,,,,,若在边上有点,使与相似,则这样的点有( )
A. 个 B. 个 C. 个 D. 个
如图,在中,点在上一点,下列条件中,能使与相似的是( )
A. B.
C. D.
如图,在 中,延长至点,使,连接交于点,交于点,则的值是( )
A. B. C. D.
如图,在中,,,四边形的面积为,则的面积是( )
A.
B.
C.
D.
将一张以为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形剪掉的两个直角三角形相似,剩下的是如图所示的四边形纸片,其中,,,,,则剪掉的两个直角三角形的斜边长不可能是( )
A. B. C. D.
如图,平面直角坐标系中,点,的坐标分别为、,是关于点的位似图形,且的坐标为,则点的坐标为( )
B.
D.
西游记的故事家喻户晓,特别是书中的孙悟空嫉恶如仇斩妖除魔大快人心在一次降妖过程中,孙悟空念动咒语将一片树叶放大后射向妖魔假如这个过程可以看成是在平面直角坐标系中的一次无旋转的变换,设变化前树叶尖部点坐标为,在咒语中变化后得到对应点为则变化后树叶的面积变为原来的( )
A. 倍 B. 倍 C. 倍 D. 倍
如图,在台球桌上,一球被击打后,从点出发,沿方向运动,撞击至点后,沿方向运动,撞击至点后,再沿方向运动,撞击至点若,,,则的长为( )
A. B. C. D.
下面是嘉嘉在实践课题“相似三角形在生活中的应用”中的一篇报告,其中指示牌,的高度被墨迹污染了.
课题 测量广场上景观灯的高度
测量示意图 说明:,点,,在同一水平线上,竖立在地面上的指示牌,高度相同,均为,两指示牌相距,影长,分别为,.
结论 景观灯的高度为.
被污染的数字为( )
A. B. C. D.
图是装了液体的高脚杯示意图数据如图,用去一部分液体后如图所示,此时液面( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
如图,在中,,,为中点,在线段上,,则______.
如图,平分,,,当 时,∽.
如图,已知点、分别在边、上,,,那么: .
如图,为测量学校旗杆的高度,小东用长为的竹竿做测量工具.移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距,与旗杆相距,则旗杆的高为______
三、解答题(本大题共9小题,共72.分)
如果有一条直线经过三角形的某个顶点,将三角形分成两个三角形,其中一个三角形与原三角形相似,则称该直线为三角形的“自相似分割线”如图,在中,,,点在边上,连接,若.
在图中求作,使得是的自相似分割线;
要求:尺规作图,不写作法,保留作图痕迹;
在的条件下,求的值.
如图,在中,点、分别是、上的点,.
若,,,求的长.
连接,作交于点,如图,求证:.
如图,,且,求证:∽.
如图,在中,,,点从点开始沿边向点以的速度移动,点从点开始沿边向点以的速度移动,如果、分别从、同时出发,那么经几秒后,点、、构成的三角形与相似
如图,在与中,点、分别在边、上,且∽,若______,则∽.
请从;;这个选项中选择一个作为条件写序号,并加以证明.
如图,已知.
尺规作图:作平行四边形;保留作图痕迹,不写作法
在所作的平行四边形中,连接,交于点.
若,,,求的长;
过点作直线与边,分别交于点,,设四边形的面积为
,平行四边形的面积为,求:的值.
如图,在平面直角坐标系中,把以格点为顶点的三角形称为格点三角形每个小方格都是边长为的正方形图中是格点三角形,点、、的坐标分别是,,.
画出关于轴对称的;
以为位似中心,在第一象限内将放大为原来的倍,得到,画出;
内有一点,直接写出经过位似变换后的对应点的坐标________________.
阳光明媚的一天实践课上,亮亮准备用所学知识测量教学楼前一座假山的高度,如图,亮亮在地面上的点处,眼睛贴地观察,看到假山顶端、教学楼顶端在一条直线上.此时他起身在处站直,发现自己的影子末端和教学楼的影子末端恰好重合于点处,测得米,亮亮的身高为米.假山的底部处因有花园围栏,无法到达,但经询问和进行部分测量后得知,米,点、、、在一条直线上,,,,已知教学楼的高度为米,请你求出假山的高度.
如图,在相对的两栋楼中间有一堵墙,甲、乙两人分别在这两栋楼内观察这堵墙,视线如图所示根据实际情况画出平面图形如图,甲从点可以看到点处,乙从点可以看到点处,是的中点,墙高,,,求甲、乙两人的观测点到地面的距离之差.
答案和解析
1.【答案】
【解析】解:由,可以假设,则,,
四边形是平行四边形,
,,,
,
故选:.
由,可以假设,则,,证明,,再利用平行线分线段成比例定理即可解决问题.
本题考查平行四边形的性质,解题的关键是学会利用参数解决问题,属于中考常考题型.
2.【答案】
【解析】解:由作法得平分,垂直平分,
,,,
,
,
,
,
同理可得,
四边形为平行四边形,
而,
四边形为菱形,
,
,
,即,
.
故选:.
利用作法得平分,垂直平分,所以,,,再证明四边形为菱形得到,然后利用平行线分线段成比例定理计算的长.
本题考查了作图复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了角平分线的性质和垂直平分线的性质.
3.【答案】
【解析】解:.,
,
.
设的长为,则长为.
若边上存在点,使与相似,那么分两种情况:
若∽,则::,
即::,
解得:
若∽,则::,
即::,
整理得:,
,
这种情形不存在,
满足条件的点的个数是个,
故选:.
根据已知分两种情况∽或∽来进行分析,求得的长,从而确定存在的个数.
此题考查了相似三角形的判定,依据相似三角形的判定定理列出关于的方程是解题的关键.
4.【答案】
【解析】解:选项A、、的条件无法判断与相似.
正确答案是D理由如下:
,
,
,
∽两边成比例夹角相等的两个三角形相似.
故选:.
根据两边成比例夹角相等的两个三角形相似,即可判断.
本题考查相似三角形的判定和性质,解题的关键是灵活运用所学知识解决问题,属于基础题,中考常考题型.
5.【答案】
【解析】解:四边形是平行四边形,
,,
∽,
,
,
,
,
,
,
,
∽,
,
故选:.
根据平行四边形的性质得出,利用相似三角形的判定和性质解答即可.
此题考查平行四边形的性质,关键是根据相似三角形的判定和性质解答.
6.【答案】
【解析】解:,
∽,
,
.
,即,
.
故选:.
由可得出∽,利用相似三角形的性质可得出,结合即可得出关于的一元一次方程,解之即可得出结论.
本题考查了相似三角形的判定与性质,利用相似三角形的性质,找出是解题的关键.
7.【答案】
【解析】解:如右图所示,
由已知可得,∽,
则,
设,,
则,
解得,
,故选项B不符合题意;
,故选项D不符合题意;
如图所示,
由已知可得,∽,
则,
设,,
则,
解得,
,故选项C不符合题意;
,
故选:.
根据题意,画出相应的图形,然后利用相似三角形的性质和分类讨论的方法,求出剪掉的两个直角三角形的斜边长,然后即可判断哪个选项符合题意.
本题考查相似三角形的性质、矩形的性质,解答本题的关键是明确题意,利用分类讨论的方法解答.
8.【答案】
【解析】
【分析】
本题考查的是位似变换的概念和性质、相似三角形的性质,如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行或共线,那么这样的两个图形叫做位似图形.
过点作轴于点,作轴于点,根据位似变换的性质得到,根据相似三角形的性质列出比例式,计算即可.
【解答】
解:过点作轴于点,过作轴于点,
则,
由题意得,,,
点、的坐标分别为、,是关于的的位似图形,且的坐标为,
,
,
,
∽,
,即,
解得,,,
,
则点的坐标为,
故选:.
9.【答案】
【解析】
【分析】
树叶端点变为,可拆分为两次变换所得,第一次是位似变换,第二次是平移变换.平移变换可决定树叶最终的位置,而面积只与位似变换有关,所以只需考虑位似变换即可得答案.
本题主要考查几何变换类型,解题的关键是根据对应点的坐标判断出其几何变换类型.
【解答】
解:由点经过变换后得到的对应点为为知,
此树叶所作的变换是位似变换和平移变换,变换的位似比为:,
则原树叶的面积与变换后的树叶的面积比为:,
故选D.
10.【答案】
【解析】
【分析】
本题主要考查相似三角形的应用,根据题意求出∽,由即可求出的长度.
【解答】
解:由题意知,
,
,
,
,
,
∽,
,
即,
,
11.【答案】
【解析】
【分析】
本题主要考查的是相似三角形的应用的有关知识,由题意可知,,利用相似三角形的判定和性质得到,,根据得到,设,进而得到,求出,进而求出即可.
【解答】
解:由题意可知,,
∽,∽,
,,
,
,
设,则,
,
.
.
12.【答案】
【解析】解:如图:过作,垂足为,过作,垂足为,
,
∽,即相似比为,
,
,,
,
,
故选:.
高脚杯前后的两个三角形相似.根据相似三角形的判定和性质即可得出结果.
本题考查相似三角形的应用,解本题的关键熟练掌握相似三角形的判定与性质.
13.【答案】
【解析】解:为中点,
.
当时,.
故答案是:.
利用平行线截线段成比例解答.
本题主要考查了平行线分线段成比例,平行于三角形的一边,并且和其他两边或两边的延长线相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.
14.【答案】
【解析】 平分,
,
当时,∽ ,
,舍,.
15.【答案】
【解析】解:,
::,
,
∽,
,
::.
和的高相同,设这个高为,
:,
故答案为:.
根据,求出:的值,再根据相似三角形的性质求得:,最后再根据面积之比即可求解.
本题主要考查了相似三角形的判定和性质,找准对应线段是解题的关键.
16.【答案】
【解析】解:因为,所以∽,
于是,即,解得:.
旗杆的高为.
易证∽,利用相似三角形的对应边成比例,列出方程求解即可.
本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程即可求出旗杆的高度.
17.【答案】解:如图,线段即为所求;
设.
,,
,
由作图可知,
,
,
,
,,
∽,
,
,
,
或,
经检验:是分式方程的解,且符合题意,
,
.
【解析】作线段的垂直平分线交于点,连接即可;
设利用相似三角形的性质构建方程求解即可.
本题考查作图相似变换,等腰三角形的性质,分式方程等知识,解题关键是理解题意,学会利用参数构建方程解决问题,属于中考常考题型.
18.【答案】解:如图,,
,即,
,
证明:如图,
,
,
,
,
,
.
【解析】本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.
如图,根据平行线分线段成比例定理得到,则利用比例性质可计算出的长,然后计算即可
由得到,由得到,利用等量代换得,然后利用比例的性质可得到结论.
19.【答案】证明:,
.
又,
,即,
∽.
【解析】由已知条件得到:,则由“两边及夹角法”证得结论.
本题考查了相似三角形的判定.
平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;
三边法:三组对应边的比相等的两个三角形相似;
两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;
两角法:有两组角对应相等的两个三角形相似.
20.【答案】解: 设经过后,,
根据已知条件,可得,.
,,,解得
设经过后,.
,,
,解得.
故经过或后,与相似.
【解析】本题考查了相似三角形的判定,利用分类思想解决问题是本题的关键分两种情况讨论,可得,或,可求的值.
21.【答案】
【解析】解:.
理由如下:∽,
,
,
,,,
,
∽.
利用相似三角形的判定:两角对应相等的两个三角形相似可证明.
本题主要考查相似三角形的判定,掌握相似三角形的判定条件是解题的关键.
22.【答案】解:如图所示,
即为所求;
如图,
四边形是平行四边形,,
,,
,,
,
;
如图,
四边形是平行四边形,
,,
,
≌,
,
,
四边形是平行四边形,
,,
,,
≌,
,
,
,
:.
【解析】分别以、为圆心,、为半径画弧,两弧交于点,连接、,即可得到平行四边形;
由平行四边形的性质得出,,由勾股定理得出,即可求出;
先证明≌,得出,即可得出,再证明≌,得出,得出,进而得出,即可得出:.
本题考查了作图复杂作图,平行四边形的判定与性质,勾股定理,熟练掌握平行四边形的判定与性质,基本作图,全等三角形的判定与性质,勾股定理等知识是解决问题的关键.
23.【答案】解:如图:即为所求
如图:即为所求
【解析】
【分析】
本题考查了作图位似变换:画位似图形的一般步骤为:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.也考查了轴对称变换.
利用网格特点和轴对称的性质画出点、、,从而得到;
根据位似图形的性质得出对应点坐标、、顺次连接即可;
根据点、、的坐标变化规律,进而得出旋转变换后的对应点的坐标.
【解答】
解:,见答案
点、、的坐标分别是、、,
点、、的坐标分别是、、,
内有一点,经过旋转变换后的对应点的坐标为;.
24.【答案】解:,,
,
∽,
,即,
解得.
,,
,
∽,
,即,
解得,
假山的高度为米.
【解析】依据∽,可得,进而得出米.再根据∽,可得,进而得出假山的高度为米.
本题主要考查了相似三角形的应用,测量不能到达顶部的物体的高度,通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.
25.【答案】解:由题意可知,
又是公共角,
∽,
,
,是的中点,
.
,,
.
又,为公共角
∽
,
.
.
甲、乙两人的观测点到地面的距离之差约为.
【解析】本题主要考查了相似三角形的应用,熟练掌握相似三角形的判定定理和性质定理是解决此题的关键.
首先证明∽,则可得,由是的中点,可得,则,由此即可求出的长,同理可求得的长,然后作差即可.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
