第1章《我们与数学同行》专题强化训练

——《我们与数学同行》专题强化训练
一、选择题
1．如图，一串有趣的图案按一定的规律排列，请仔细观察，按此规律第2 010个图案是(　　)
2．观察下列算式：31＝3,32＝9,33＝27,34＝81,35＝243,36＝729,37＝2 187,38＝6 561，…通过观察，用你所发现的规律确定32 000的个位数字是(　　)
A．3 B．9 C．7 D．1
3．在下面各正方形中的四个数之间都有相同的规律，根据此规律，m的值是(　　)
A．38 B．52 C．66 D．74
4.图1是一个边长为1的等边三角形和一个菱形的组合图形，菱形边长为等边三角形边长的一半，以此为基本单位，可以拼成一个形状相同但尺寸更大的图形（如图2），依此规律继续拼下去（如图3），……，则第n个图形的周长是( )
（A） （B） （C） （D）
5．寸是电视机常用规格之一,1寸约为拇指上面一节的长,则7寸长相当于( )
A.课本的宽度 B.粉笔的长度
C.课桌的宽度 D.黑板的高度
6 ．一个两位数,十位上的数字比个位上的数字大6那么这样的两位数共有( )
A.1个 B.2个 C.3个 D.4个
7 ．2008年5月12日,在四川省汶川县发生8.0级特大地震,能够准确表示汶川这个地点位置的是( )
A.北纬31o B.东经103.5o C.金华的西北方向上 D.北纬31o,东经103.5o
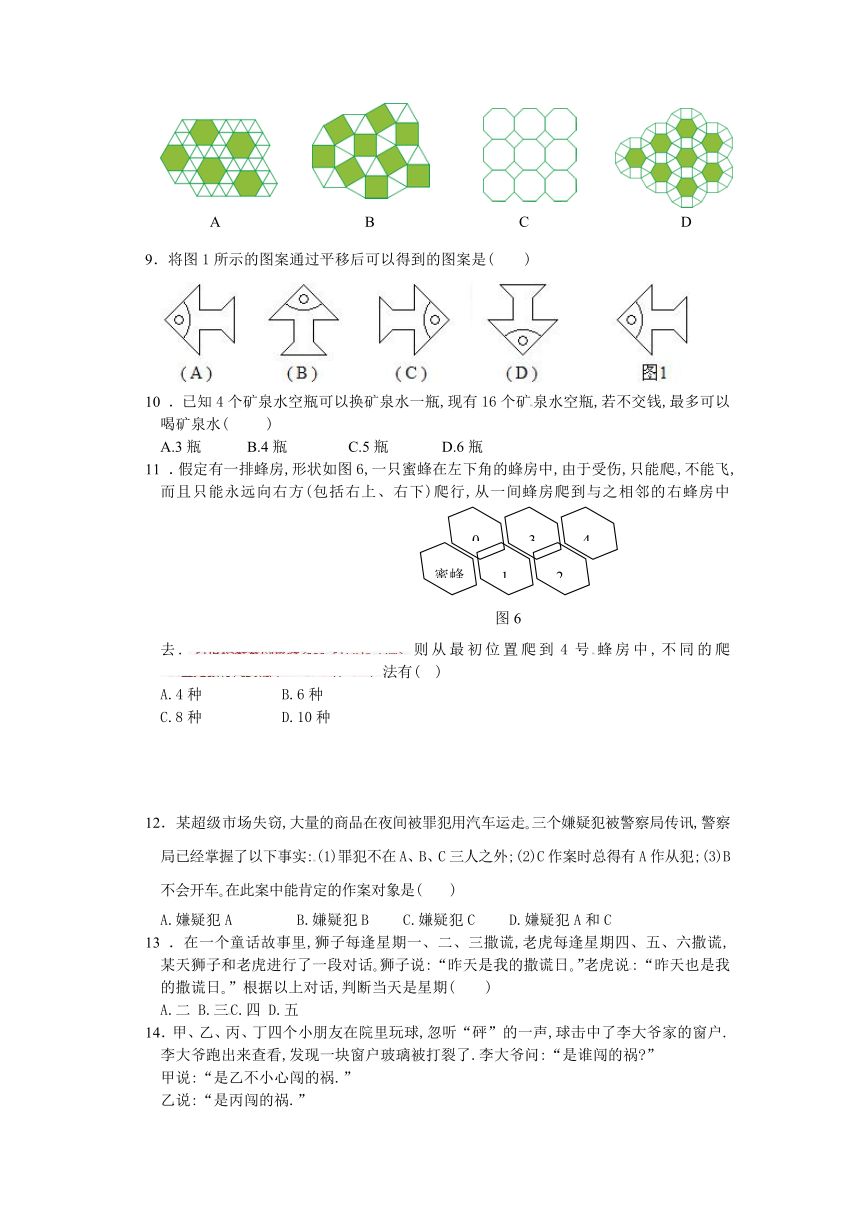
8．下述美妙的图案中,是由正三角形、正方形、正六边形、正八边形中的三种镶嵌而成的为
9．将图1所示的图案通过平移后可以得到的图案是( )
10 ．已知4个矿泉水空瓶可以换矿泉水一瓶,现有16个矿泉水空瓶,若不交钱,最多可以喝矿泉水( )
A.3瓶 B.4瓶 C.5瓶 D.6瓶
11 ．假定有一排蜂房,形状如图6,一只蜜蜂在左下角的蜂房中,由于受伤,只能爬,不能飞,而且只能永远向右方(包括右上、右下)爬行,从一间蜂房爬到与之相邻的右蜂房中去.则从最初位置爬到4号蜂房中,不同的爬法有( )
A.4种 B.6种
C.8种 D.10种
12．某超级市场失窃,大量的商品在夜间被罪犯用汽车运走?三个嫌疑犯被警察局传讯,警察局已经掌握了以下事实:(1)罪犯不在A、B、C三人之外;(2)C作案时总得有A作从犯;(3)B不会开车?在此案中能肯定的作案对象是( )
A.嫌疑犯A B.嫌疑犯B C.嫌疑犯C D.嫌疑犯A和C
13 ．在一个童话故事里,狮子每逢星期一、二、三撒谎,老虎每逢星期四、五、六撒谎,某天狮子和老虎进行了一段对话?狮子说:“昨天是我的撒谎日?”老虎说:“昨天也是我的撒谎日?”根据以上对话,判断当天是星期( )
A.二 B.三C.四 D.五
14．甲、乙、丙、丁四个小朋友在院里玩球,忽听“砰”的一声,球击中了李大爷家的窗户.李大爷跑出来查看,发现一块窗户玻璃被打裂了.李大爷问:“是谁闯的祸?”
甲说:“是乙不小心闯的祸.”
乙说:“是丙闯的祸.”
丙说:“乙说的不是实话.”
丁说:“反正不是我闯的祸.”
如果这四个小朋友中只有一个人说了实话,请你帮李大爷判断一下,究竟是谁闯的祸
A.甲 B. 乙 C.丙 D.丁
二、填空题
15．用围棋子按下面的规律摆图形，则摆第n个图形需要围棋子的枚数是________．
16．阅读下列材料：
1×2＝(1×2×3－0×1×2)， 2×3＝(2×3×4－1×2×3)， 3×4＝(3×4×5－2×3×4)，
由以上三个等式相加，可得 1×2＋2×3＋3×4＝×3×4×5＝20.
读完以上材料，请你计算下列各题：
(1)1×2＋2×3＋3×4＋…＋10×11(写出过程)；
(2)1×2＋2×3＋3×4＋…＋n×(n＋1)＝________；
(3)1×2×3＋2×3×4＋3×4×5＋…＋7×8×9＝________.
17．观察下列图形：
它们是按一定规律排列的，依照此规律，第9个图形中共有________个★.
18．如图，将第一个图(图①)所示的正三角形连结各边中点进行分割，得到第二个图(图②)；再将第二个图中最中间的小正三角形按同样的方式进行分割，得到第三个图(图③)；再将第三个图中最中间的小正三角形按同样的方式进行分割，…则得到的第五个图中，共有________个正三角形．
19．如图为手的示意图，在各个手指间标记字母A，B，C，D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4，…，当数到12时，对应的字母是________；当字母C第201次出现时，恰好数到的数是________；当字母C第2n＋1次出现时(n为正整数)，恰好数到的数是________．(用含n的代数式表示)
20．一个正方形要绕它的中心至少旋转_________度才能和原来的图形重合.
21．有一个两位数,它的十位数字与个位数字之和为5,则符合条件的数有________个.
22．本学期,我们做过“抢30”的游戏,如果将游戏规则中“不可以连说三个数,谁先抢到30谁就获胜”,改为“每次可以连说三个数,谁先抢到33谁就获胜”,那么采取适当策略,其结果_________者胜.
23．乘火车从A站出发,沿途经过3个车站方可到达B站,那么在A、B两站之间需要安排不同的车票__________种?
24．将一根绳子两端分别涂上红色和白色,再在中间随意画3个圆点, 涂上白色或红色,然后在这三个圆点处把绳子剪断,这样所得到的各小段两端都有颜色.则两端颜色不同的小段数目一定是________(答奇数或偶数)_________________.
25．填在下面三个田字格内的数有相同的规律,根据此规律,请填出图4中的数字.
图1 图2 图3 图4
附：参考答案
一、选择题
1.【解析】观察图案可知，每4个图案循环一次，因为2 010÷4＝502……2，所以第2 010个图案与第2个图案相同，故选B.
【答案】B
2.【解析】观察算式，可发现每4个数字的个位数字循环一次，因为2 000÷4＝500，故
32 000的个位数字是1.
【答案】D
3.【解析】规律一：和m对应的位置除外，其他相应位置的数都是偶数，且后面的数比对应的前面的数大2.如0,2,4,6，则其他位置的数是4,6,8,10；2,4,6,8.如图
规律二：一条对角线位置的数字之和等于另一条对角线位置的数字之积．如4＋44＝6×8，则6＋m＝8×10，故m＝74.
【答案】D
4. 【答案】C
5．【答案】A
6．【答案】D
7．【答案】D
8．【答案】D
9．【答案】A
10．【答案】C
11．【答案】C
12．【答案】A
13 ．【答案】C
14．【答案】D
二、填空题
15.【解析】第1个图形为5＝3×1＋2，第2个图形为5＋3＝3×2＋2，……第n个图形为3n＋2.
【答案】3n＋2
16.【答案】(1)1×2＋2×3＋3×4＋…＋10×11
＝(1×2×3－0×1×2)＋(2×3×4－1×2×3)＋(3×4×5－2×3×4)＋…＋(10×11×12－9×10×11)
＝×1×2×3＋×2×3×4－×1×2×3＋…＋×10×11×12－×9×10×11＝×10×11×12＝440.
(2)×n×(n＋1)×(n＋2)
(3)1 260
17.【解析】规律是1＋3×1,1＋3×2,1＋3×3，…，1＋3×9，所以第9个图形共有1＋3×9＝1＋27＝28(个)．
【答案】28
18.【解析】图①中有1个正三角形；图②中有5个正三角形，即1＋4×1；图③中有9个正三角形，即1＋4＋4＝1＋4×2；…，依此规律，图⑤中有1＋4×4＝17个正三角形．
【答案】17
19【解析】当数到12时，对应的字母是B.根据已知条件将字母进行排列，发现字母C出现的次数是奇数时，此时数到的数字恰好是这个奇数的3倍.201,2n＋1都是奇数，则数到的数字分别是3×201＝603,3(2n＋1)＝6n＋3.
【答案】B　603　6n＋3
20．90°.
21．答案:5个
22．先走
23．20
24．奇数;

三、解答题
26．略.
27 (1)
(2)