北师大版数学九上1.1.3菱形的性质与判定综合应用 学案(无答案)
文档属性
| 名称 | 北师大版数学九上1.1.3菱形的性质与判定综合应用 学案(无答案) | 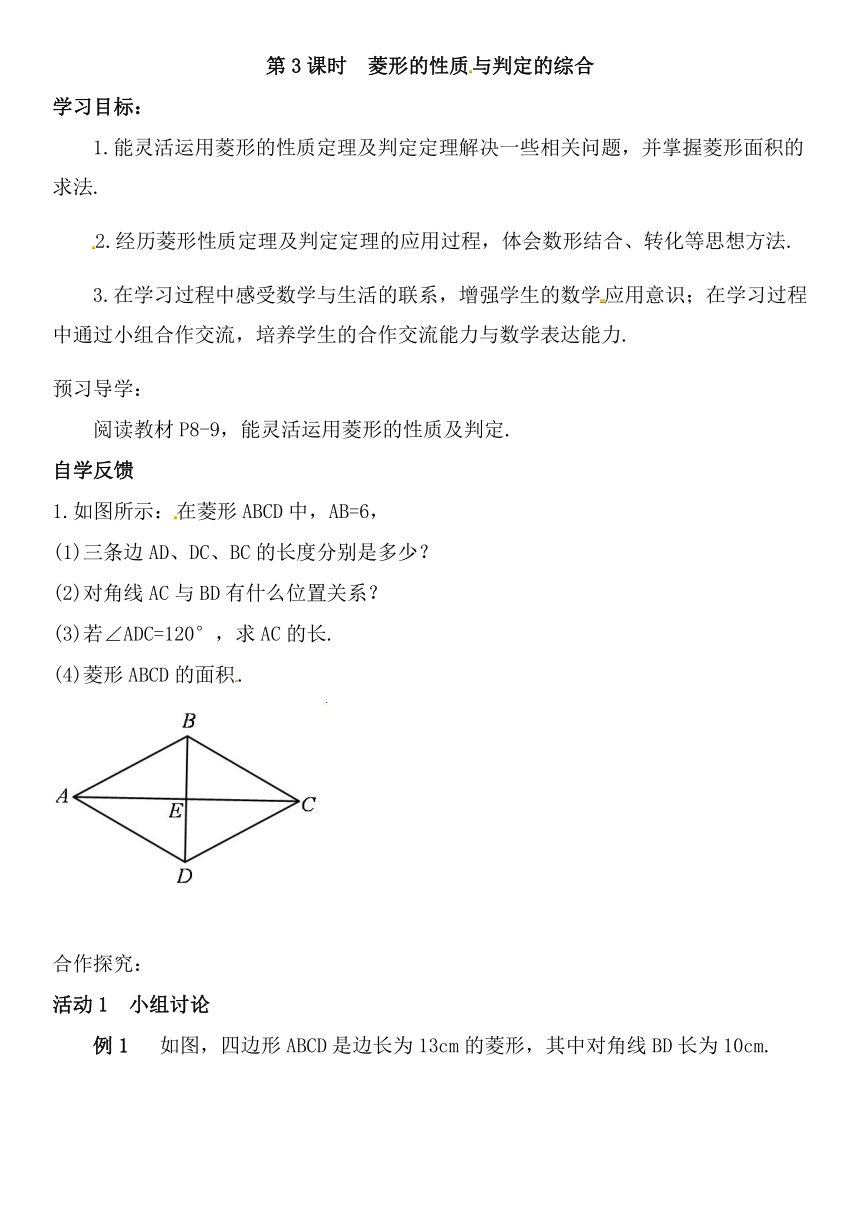 | |
| 格式 | doc | ||
| 文件大小 | 112.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 20:38:22 | ||
图片预览

文档简介
菱形的性质与判定的综合
学习目标:
1.能灵活运用菱形的性质定理及判定定理解决一些相关问题,并掌握菱形面积的求法.
2.经历菱形性质定理及判定定理的应用过程,体会数形结合、转化等思想方法.
3.在学习过程中感受数学与生活的联系,增强学生的数学应用意识;在学习过程中通过小组合作交流,培养学生的合作交流能力与数学表达能力.
预习导学:
阅读教材P8-9,能灵活运用菱形的性质及判定.
自学反馈
1.如图所示:在菱形ABCD中,AB=6,
(1)三条边AD、DC、BC的长度分别是多少?
(2)对角线AC与BD有什么位置关系?
(3)若∠ADC=120°,求AC的长.
(4)菱形ABCD的面积.
合作探究:
活动1 小组讨论
例1 如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长为10cm.
求:(1)对角线AC的长度;
(2)菱形ABCD的面积.
解:(1)∵四边形ABCD是菱形,
∴AC⊥BD,即∠AED=90°,
DE=BD×10=5(cm)
∴在Rt△ADE中,由勾股定理可得:
∴AC=2AE=2×12=24(cm).
(2)S菱形ABCD= S△ABD+ S△CBD
=2×S△ABD=2××BD×AE
= BD×AE=10×12=120(cm2).
注意:菱形的面积除了以上求法,还可以用对角线相乘除以2.
活动2 跟踪训练
1.如图,菱形ABCD的周长为40cm,它的一条对角线BD长10cm,则∠ABC= °,
AC= cm.
2.如图,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=4cm,BD=8cm,则这个菱形的面积是 cm2.
3. 如图,四边形ABCD中,AB=AC=AD,BC=CD,锐角∠BAC的角平分线AE交BC于点E,AF是CD边上的中线,且PC⊥CD与AE交于点P,QC⊥BC与AF交于点Q.求证:四边形APCQ是菱形.
课堂小结
通过本节课的学习你有哪些收获,你还存在什么疑问?
学习目标:
1.能灵活运用菱形的性质定理及判定定理解决一些相关问题,并掌握菱形面积的求法.
2.经历菱形性质定理及判定定理的应用过程,体会数形结合、转化等思想方法.
3.在学习过程中感受数学与生活的联系,增强学生的数学应用意识;在学习过程中通过小组合作交流,培养学生的合作交流能力与数学表达能力.
预习导学:
阅读教材P8-9,能灵活运用菱形的性质及判定.
自学反馈
1.如图所示:在菱形ABCD中,AB=6,
(1)三条边AD、DC、BC的长度分别是多少?
(2)对角线AC与BD有什么位置关系?
(3)若∠ADC=120°,求AC的长.
(4)菱形ABCD的面积.
合作探究:
活动1 小组讨论
例1 如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长为10cm.
求:(1)对角线AC的长度;
(2)菱形ABCD的面积.
解:(1)∵四边形ABCD是菱形,
∴AC⊥BD,即∠AED=90°,
DE=BD×10=5(cm)
∴在Rt△ADE中,由勾股定理可得:
∴AC=2AE=2×12=24(cm).
(2)S菱形ABCD= S△ABD+ S△CBD
=2×S△ABD=2××BD×AE
= BD×AE=10×12=120(cm2).
注意:菱形的面积除了以上求法,还可以用对角线相乘除以2.
活动2 跟踪训练
1.如图,菱形ABCD的周长为40cm,它的一条对角线BD长10cm,则∠ABC= °,
AC= cm.
2.如图,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=4cm,BD=8cm,则这个菱形的面积是 cm2.
3. 如图,四边形ABCD中,AB=AC=AD,BC=CD,锐角∠BAC的角平分线AE交BC于点E,AF是CD边上的中线,且PC⊥CD与AE交于点P,QC⊥BC与AF交于点Q.求证:四边形APCQ是菱形.
课堂小结
通过本节课的学习你有哪些收获,你还存在什么疑问?
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
