《数与形结合的规律》同步练习六年级上册数学人教版(含答案)
文档属性
| 名称 | 《数与形结合的规律》同步练习六年级上册数学人教版(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 324.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-25 22:09:25 | ||
图片预览



文档简介
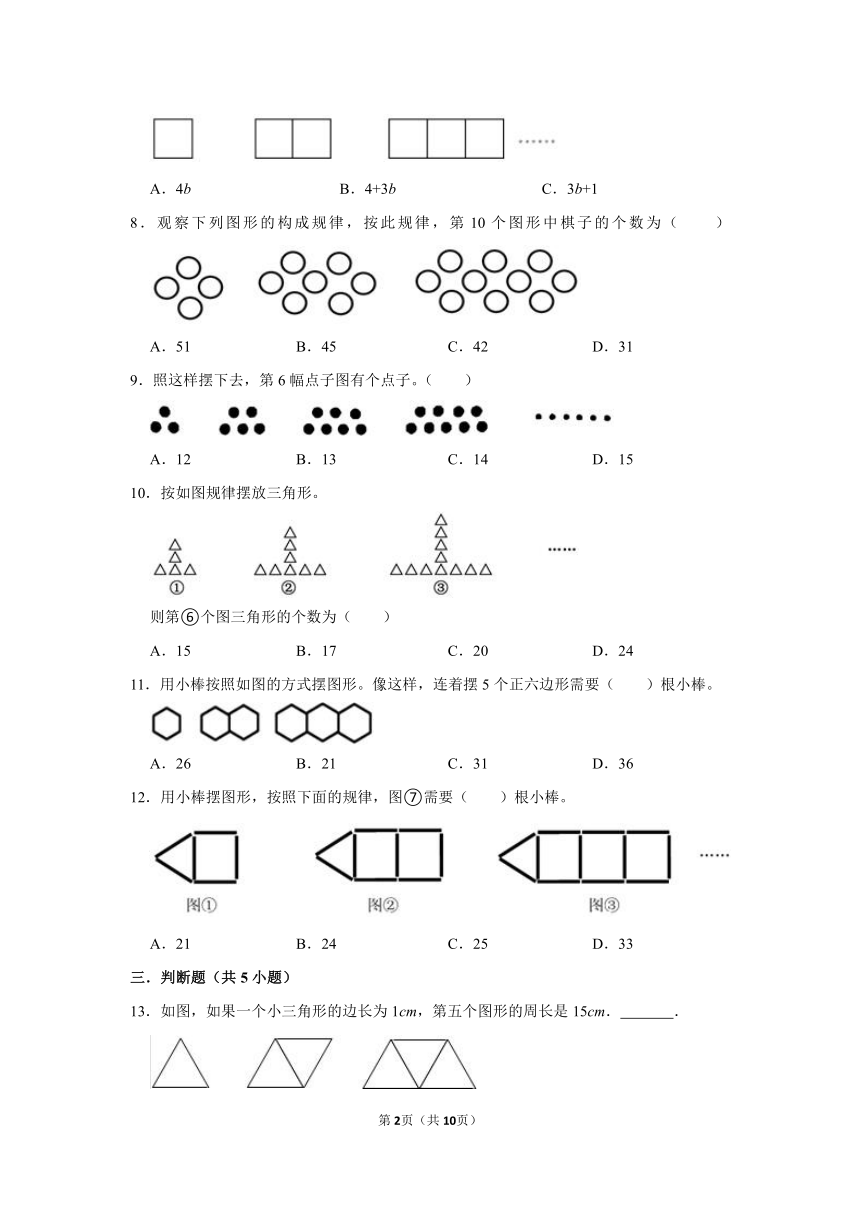
《数与形结合的规律》(同步练习)-六年级上册数学人教版
一.填空题(共6小题)
1.如图,用小棒摆小鱼图案,照这样的规律摆下去,摆到第7个图案需要 根小棒。
2.观察下面的点阵图的规律,第5个点阵图中有 个点,第n个这样的点阵图中有 个点。
3.观察如图,想一想。第20幅图有 个棋子,第n幅图有 个棋子。
4.“转化”是解决问题的常用策略之一,有时画图可以帮助我们找到转化的方法。例如借助图,可以将算式转化成: 。(写出算式并计算出结果)
5.像这样摆下去,摆n个正方形需要 根小棒。
6.在△△〇□△△〇□△△〇□△△〇□……中,第56个图形是 ,第78个图形是 。
二.选择题(共6小题)
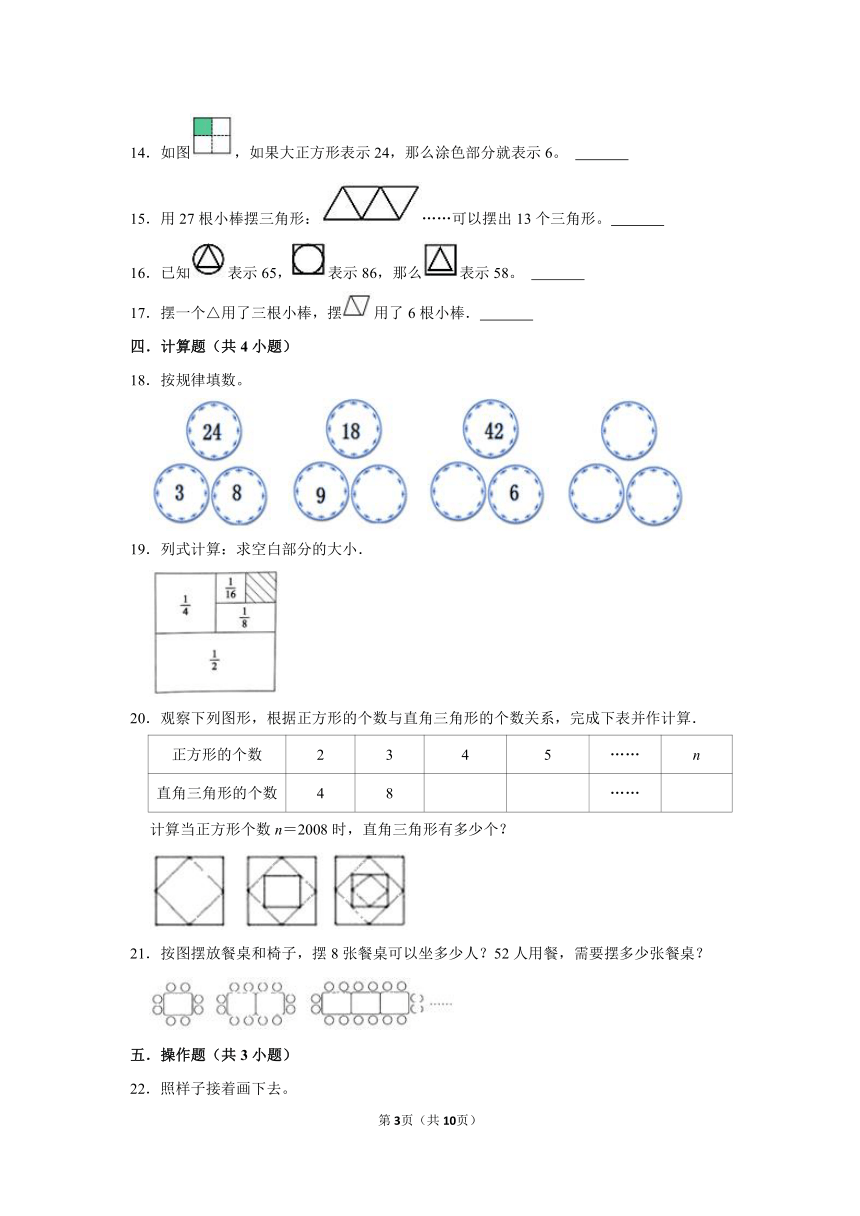
7.如图,摆1个正方形要用4根小棒,摆2个正方形要用7根小棒,那么摆b个正方形要用( )根小棒。
A.4b B.4+3b C.3b+1
8.观察下列图形的构成规律,按此规律,第10个图形中棋子的个数为( )
A.51 B.45 C.42 D.31
9.照这样摆下去,第6幅点子图有个点子。( )
A.12 B.13 C.14 D.15
10.按如图规律摆放三角形。
则第⑥个图三角形的个数为( )
A.15 B.17 C.20 D.24
11.用小棒按照如图的方式摆图形。像这样,连着摆5个正六边形需要( )根小棒。
A.26 B.21 C.31 D.36
12.用小棒摆图形,按照下面的规律,图⑦需要( )根小棒。
A.21 B.24 C.25 D.33
三.判断题(共5小题)
13.如图,如果一个小三角形的边长为1cm,第五个图形的周长是15cm. .
14.如图,如果大正方形表示24,那么涂色部分就表示6。
15.用27根小棒摆三角形:……可以摆出13个三角形。
16.已知表示65,表示86,那么表示58。
17.摆一个△用了三根小棒,摆用了6根小棒.
四.计算题(共4小题)
18.按规律填数。
19.列式计算:求空白部分的大小.
20.观察下列图形,根据正方形的个数与直角三角形的个数关系,完成下表并作计算.
正方形的个数 2 3 4 5 …… n
直角三角形的个数 4 8 ……
计算当正方形个数n=2008时,直角三角形有多少个?
21.按图摆放餐桌和椅子,摆8张餐桌可以坐多少人?52人用餐,需要摆多少张餐桌?
五.操作题(共3小题)
22.照样子接着画下去。
23.规律的积累者。
如图是一张破损的长方形纸,这张纸原来的面积是 ,从这张纸上裁下一个最大的正方形,正方形的面积是 。
(请在如图上画出最大的正方形)
24.画一画,算一算。
(1)请你在横线上画出第4个点阵。
(2)第15个点阵中有 点。
六.解答题(共1小题)
25.在生产、生活中,我们经常把一些同样的圆柱捆扎起来,下面我们来探究捆扎时怎样求绳子的长度。假设每个圆柱管的直径都是10厘米,当圆柱管的放置方式是“单层平放”时,捆扎后的横截面如下图所示,请你根据已知数据(接头不算),先在方框中画一画,再把表格中缺少的数据填写完整。
圆柱管个数(个) 1 2 3 … 6
绳子长度(厘米) 31.4 51.4 …
《数与形结合的规律》(同步练习)-六年级上册数学人教版
参考答案与试题解析
一.填空题(共6小题)
1.【解答】解:6×7+2
=42+2
=44(根)
答:摆到第7个图案需要44根小棒。
故答案为:44。
2.【解答】解:3×5+3
=15+3
=18(个)
答:第5个点阵图中有18个点,第n个这样的点阵图中有(3n+3)个点。
故答案为:18,(3n+3)。
3.【解答】解:20×1+20×(20﹣1)×(3﹣1)÷2
=20+20×19×2÷2
=20+380
=400(个)
n×1+n(n﹣1)×(3﹣1)÷2
=n+n ﹣n
=n
答:第20幅图有400,第n幅图有n 个棋子。
故答案为:400,n 。
4.【解答】解:由分析可知,=1﹣=。
故答案为:1﹣=。
5.【解答】解:摆1个正方形需要小棒:(1+3)根;
摆2个正方形需要小棒:(1+2×3)根;
摆3个正方形需要小棒:(1+3×3)根;
……
摆n个正方形需要小棒:(1+3n)根。
故答案为:(3n+1)。
6.【解答】解:56÷4=14(个)
78÷4=19(个)……2(个)
答:第56个图形是□,第78个图形是△。
故答案为:□,△。
二.选择题(共6小题)
7.【解答】解:摆b个正方形要用(3b+1)根小棒。
故选:C。
8.【解答】解:根据分析可得,
3×10+1
=30+1
=31(个)
答:第10个图形中棋子的个数为31个.
故选:D.
9.【解答】解:1+6×2
=1+12
=13(个)
答:第6幅点子图有13个点子。
故选:B。
10.【解答】解:图①三角形的个数:2×3﹣1=5(个)
图②三角形的个数:3×3﹣1=8(个)
图③三角形的个数:4×3﹣1=11(个)
……
图n三角形的个数:3(n+1)﹣1=(3n+2)个
……
第⑥个图三角形的个数为:
3×6+2
=18+2
=20(个)
答:第⑥个图三角形的个数为20个.
故选:C。
11.【解答】解:由分析可知,摆n个六边形需要的小棒数为:(1+5n)根。
当n=5时,
1+5×5
=1+25
=26(根)
答:连着摆5个正六边形需要26根小棒。
故选:A。
12.【解答】解:8×3=24(根)
答:图⑦需要24根小棒。
故选:B。
三.判断题(共5小题)
13.【解答】解:根据题干分析可得:当有n个三角形时,图形周长=边长×(n+2),
当n=5时,图形周长是:1×(5+2)=7(cm),
答:第五个图形的周长是7cm.
故答案为:×.
14.【解答】解:24÷4=6
所以原说法正确。
故答案为:√。
15.【解答】解:摆1个三角形需要小棒3根
摆2个三角形需要小棒:3+2=5(根)
摆3个三角形需要小棒:3+2+2=7(根)
……
摆13个三角形需要小棒:
3+12×2
=3+24
=27(根)
答:27根小棒可以摆13个三角形。所以原题说法正确。
故答案为:√。
16.【解答】解:由题意可知:〇表示6,△表示5,□表示8,所以表示85,所以原题说法错误。
故答案为:×。
17.【解答】解:3+(n﹣1)×2
=3+1×2
=5
所以题干的说法是错误的.
故答案为:×.
四.计算题(共4小题)
18.【解答】解:18÷9=2
42÷6=7
如图:
(最后一组答案不唯一。)
19.【解答】解:+++
=1﹣
=
20.【解答】解:2个正方形,分成了可以写作4×(2﹣1)=4个直角三角形;
3个正方形,分成了4×(3﹣1)=8个直角三角形;
4个正方形,分成了4×(4﹣1)=12个直角三角形…
5个正方形,分成了4×(5﹣1)=16个直角三角形…
则n个正方形可以分成4×(n﹣1)个直角三角形;
由此可以完成表格如下图所示:
正方形的个数 2 3 4 5 …… n
直角三角形的个数 4 8 12 16 …… 4×(n﹣1)
当正方形的个数为2008个,即n=2008时,直角三角形的个数为:
4×(2008﹣1)
=4×2007
=8028(个)
答:当正方形的个数n=2008时,直角三角形有8028个.
21.【解答】解:第一张餐桌上可以摆放8把椅子,
进一步观察发现:多一张餐桌,多放4把椅子.
所以第n张餐桌共有4+4n把椅子,
(1)当n=8时,
4+4×8=36(人),
答:摆8张餐桌可以坐36人.
(2)当52人用餐时,
则,4+4n=52
4n=48
n=12
答:52人用餐,需要摆12张餐桌.
五.操作题(共3小题)
22.【解答】解:
23.【解答】解:(1)10×3=30(平方分米)
(2)3×3=9(平方分米)
答:这张纸原来的面积是30平方分米,从这张纸上裁下一个最大的正方形,正方形的面积是9平方分米。
故答案为:30平方分米;9平方分米。
24.【解答】解:(1)4×5=20(个)
如图:
(2)第15个点阵点子的个数是:
15×16=240(个)
答:第15个点阵中有240点。
故答案为:240。
六.解答题(共1小题)
25.【解答】解:
10×3.14+(3﹣1)×2×10
=31.4+40
=71.4(厘米)
10×3.14+(6﹣1)×2×10
=31.4+100
=131.14(厘米)
圆柱管个数(个) 1 2 3 … 6
绳子长度(厘米) 31.4 51.4 71.4 … 131.4
故答案为:71.4,131.4。
第1页(共1页)
一.填空题(共6小题)
1.如图,用小棒摆小鱼图案,照这样的规律摆下去,摆到第7个图案需要 根小棒。
2.观察下面的点阵图的规律,第5个点阵图中有 个点,第n个这样的点阵图中有 个点。
3.观察如图,想一想。第20幅图有 个棋子,第n幅图有 个棋子。
4.“转化”是解决问题的常用策略之一,有时画图可以帮助我们找到转化的方法。例如借助图,可以将算式转化成: 。(写出算式并计算出结果)
5.像这样摆下去,摆n个正方形需要 根小棒。
6.在△△〇□△△〇□△△〇□△△〇□……中,第56个图形是 ,第78个图形是 。
二.选择题(共6小题)
7.如图,摆1个正方形要用4根小棒,摆2个正方形要用7根小棒,那么摆b个正方形要用( )根小棒。
A.4b B.4+3b C.3b+1
8.观察下列图形的构成规律,按此规律,第10个图形中棋子的个数为( )
A.51 B.45 C.42 D.31
9.照这样摆下去,第6幅点子图有个点子。( )
A.12 B.13 C.14 D.15
10.按如图规律摆放三角形。
则第⑥个图三角形的个数为( )
A.15 B.17 C.20 D.24
11.用小棒按照如图的方式摆图形。像这样,连着摆5个正六边形需要( )根小棒。
A.26 B.21 C.31 D.36
12.用小棒摆图形,按照下面的规律,图⑦需要( )根小棒。
A.21 B.24 C.25 D.33
三.判断题(共5小题)
13.如图,如果一个小三角形的边长为1cm,第五个图形的周长是15cm. .
14.如图,如果大正方形表示24,那么涂色部分就表示6。
15.用27根小棒摆三角形:……可以摆出13个三角形。
16.已知表示65,表示86,那么表示58。
17.摆一个△用了三根小棒,摆用了6根小棒.
四.计算题(共4小题)
18.按规律填数。
19.列式计算:求空白部分的大小.
20.观察下列图形,根据正方形的个数与直角三角形的个数关系,完成下表并作计算.
正方形的个数 2 3 4 5 …… n
直角三角形的个数 4 8 ……
计算当正方形个数n=2008时,直角三角形有多少个?
21.按图摆放餐桌和椅子,摆8张餐桌可以坐多少人?52人用餐,需要摆多少张餐桌?
五.操作题(共3小题)
22.照样子接着画下去。
23.规律的积累者。
如图是一张破损的长方形纸,这张纸原来的面积是 ,从这张纸上裁下一个最大的正方形,正方形的面积是 。
(请在如图上画出最大的正方形)
24.画一画,算一算。
(1)请你在横线上画出第4个点阵。
(2)第15个点阵中有 点。
六.解答题(共1小题)
25.在生产、生活中,我们经常把一些同样的圆柱捆扎起来,下面我们来探究捆扎时怎样求绳子的长度。假设每个圆柱管的直径都是10厘米,当圆柱管的放置方式是“单层平放”时,捆扎后的横截面如下图所示,请你根据已知数据(接头不算),先在方框中画一画,再把表格中缺少的数据填写完整。
圆柱管个数(个) 1 2 3 … 6
绳子长度(厘米) 31.4 51.4 …
《数与形结合的规律》(同步练习)-六年级上册数学人教版
参考答案与试题解析
一.填空题(共6小题)
1.【解答】解:6×7+2
=42+2
=44(根)
答:摆到第7个图案需要44根小棒。
故答案为:44。
2.【解答】解:3×5+3
=15+3
=18(个)
答:第5个点阵图中有18个点,第n个这样的点阵图中有(3n+3)个点。
故答案为:18,(3n+3)。
3.【解答】解:20×1+20×(20﹣1)×(3﹣1)÷2
=20+20×19×2÷2
=20+380
=400(个)
n×1+n(n﹣1)×(3﹣1)÷2
=n+n ﹣n
=n
答:第20幅图有400,第n幅图有n 个棋子。
故答案为:400,n 。
4.【解答】解:由分析可知,=1﹣=。
故答案为:1﹣=。
5.【解答】解:摆1个正方形需要小棒:(1+3)根;
摆2个正方形需要小棒:(1+2×3)根;
摆3个正方形需要小棒:(1+3×3)根;
……
摆n个正方形需要小棒:(1+3n)根。
故答案为:(3n+1)。
6.【解答】解:56÷4=14(个)
78÷4=19(个)……2(个)
答:第56个图形是□,第78个图形是△。
故答案为:□,△。
二.选择题(共6小题)
7.【解答】解:摆b个正方形要用(3b+1)根小棒。
故选:C。
8.【解答】解:根据分析可得,
3×10+1
=30+1
=31(个)
答:第10个图形中棋子的个数为31个.
故选:D.
9.【解答】解:1+6×2
=1+12
=13(个)
答:第6幅点子图有13个点子。
故选:B。
10.【解答】解:图①三角形的个数:2×3﹣1=5(个)
图②三角形的个数:3×3﹣1=8(个)
图③三角形的个数:4×3﹣1=11(个)
……
图n三角形的个数:3(n+1)﹣1=(3n+2)个
……
第⑥个图三角形的个数为:
3×6+2
=18+2
=20(个)
答:第⑥个图三角形的个数为20个.
故选:C。
11.【解答】解:由分析可知,摆n个六边形需要的小棒数为:(1+5n)根。
当n=5时,
1+5×5
=1+25
=26(根)
答:连着摆5个正六边形需要26根小棒。
故选:A。
12.【解答】解:8×3=24(根)
答:图⑦需要24根小棒。
故选:B。
三.判断题(共5小题)
13.【解答】解:根据题干分析可得:当有n个三角形时,图形周长=边长×(n+2),
当n=5时,图形周长是:1×(5+2)=7(cm),
答:第五个图形的周长是7cm.
故答案为:×.
14.【解答】解:24÷4=6
所以原说法正确。
故答案为:√。
15.【解答】解:摆1个三角形需要小棒3根
摆2个三角形需要小棒:3+2=5(根)
摆3个三角形需要小棒:3+2+2=7(根)
……
摆13个三角形需要小棒:
3+12×2
=3+24
=27(根)
答:27根小棒可以摆13个三角形。所以原题说法正确。
故答案为:√。
16.【解答】解:由题意可知:〇表示6,△表示5,□表示8,所以表示85,所以原题说法错误。
故答案为:×。
17.【解答】解:3+(n﹣1)×2
=3+1×2
=5
所以题干的说法是错误的.
故答案为:×.
四.计算题(共4小题)
18.【解答】解:18÷9=2
42÷6=7
如图:
(最后一组答案不唯一。)
19.【解答】解:+++
=1﹣
=
20.【解答】解:2个正方形,分成了可以写作4×(2﹣1)=4个直角三角形;
3个正方形,分成了4×(3﹣1)=8个直角三角形;
4个正方形,分成了4×(4﹣1)=12个直角三角形…
5个正方形,分成了4×(5﹣1)=16个直角三角形…
则n个正方形可以分成4×(n﹣1)个直角三角形;
由此可以完成表格如下图所示:
正方形的个数 2 3 4 5 …… n
直角三角形的个数 4 8 12 16 …… 4×(n﹣1)
当正方形的个数为2008个,即n=2008时,直角三角形的个数为:
4×(2008﹣1)
=4×2007
=8028(个)
答:当正方形的个数n=2008时,直角三角形有8028个.
21.【解答】解:第一张餐桌上可以摆放8把椅子,
进一步观察发现:多一张餐桌,多放4把椅子.
所以第n张餐桌共有4+4n把椅子,
(1)当n=8时,
4+4×8=36(人),
答:摆8张餐桌可以坐36人.
(2)当52人用餐时,
则,4+4n=52
4n=48
n=12
答:52人用餐,需要摆12张餐桌.
五.操作题(共3小题)
22.【解答】解:
23.【解答】解:(1)10×3=30(平方分米)
(2)3×3=9(平方分米)
答:这张纸原来的面积是30平方分米,从这张纸上裁下一个最大的正方形,正方形的面积是9平方分米。
故答案为:30平方分米;9平方分米。
24.【解答】解:(1)4×5=20(个)
如图:
(2)第15个点阵点子的个数是:
15×16=240(个)
答:第15个点阵中有240点。
故答案为:240。
六.解答题(共1小题)
25.【解答】解:
10×3.14+(3﹣1)×2×10
=31.4+40
=71.4(厘米)
10×3.14+(6﹣1)×2×10
=31.4+100
=131.14(厘米)
圆柱管个数(个) 1 2 3 … 6
绳子长度(厘米) 31.4 51.4 71.4 … 131.4
故答案为:71.4,131.4。
第1页(共1页)
