《不等式》专题6 基本不等式最值分析(中下)专题讲义(Word版含答案)
文档属性
| 名称 | 《不等式》专题6 基本不等式最值分析(中下)专题讲义(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 684.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-26 05:18:01 | ||
图片预览




文档简介
《不等式》专题6-1 基本不等式最值分析(中下)
(6套13页)
典型例题:
若,且,则:([endnoteRef:0])
(1)的最大值为 ;(2)的最大值为 ;(3)的最大值为 ; [0: 答案:6,,12;]
不等式a2+1≥2a中等号成立的条件是([endnoteRef:1] )
A.a=±1 B.a=1 C.a=-1 D.a=0 [1: 答案:B;
[解析] a2+1-2a=(a-1)2≥0,∴a=1时,等号成立.]
若a<1,则a+与-1的大小关系是[endnoteRef:2]________. [2: 答案:a+≤-1;
解析:因为a<1,即1-a>0,所以-=(1-a)+≥2 =2.
即a+≤-1.]
若,的最大值为 [endnoteRef:3] [3: 答案:;]
(多选)设正实数,满足,则([endnoteRef:4] )
A.有最小值4 B.有最小值
C.有最大值1 D.有最小值 [4: 答案:AD;]
(多选)已知a,b>0且2a+b=1,则的值不可能是( [endnoteRef:5] )
A.7 B.8 C.9 D.10 [5: 答案:ABD;]
已知,则的最大值为 [endnoteRef:6] . [6: 答案:6;]
随堂练习:
若正实数a,b满足,则下列说法正确的是 [endnoteRef:7]
A.ab有最小值 B.有最小值
C.有最小值4 D.有最小值 [7: 【答案】C
【解析】,,且;;
;有最大值,选项A错误;
,,即有最大值,B项错误.
,有最小值4,C正确;
,的最小值是,不是,D错误.
]
已知aA.3 B.2 C.4 D.1 [8: A 解析:因为a0,
由基本不等式可得+b-a=1++(b-a)≥1+2=3,
当且仅当=b-a(b>a),即当b-a=1时,等号成立,因此,+b-a的最小值为3,故选A.]
已知不等式(x+y)≥9对任意x、y为正实数恒成立,则正数a的最小值为____[endnoteRef:9]____.
[9: 答案:4;
[解析] 展开后,利用基本不等式,而后解不等式可求a值.
∵(x+y)=1+++a≥a+1+2(a>0),∴要使原不等式恒成立,则只需a+1+2≥9,即(-2)(+4)≥0,故≥2,即a≥4,∴正数a的最小值是4.
]
(2020·浙江鄞州·宁波华茂外国语学校高三一模)已知实数,,,则的最小值是( [endnoteRef:10] ) A. B. C. D. [10: 【答案】B
【解析】
∵,,
∴
当且仅当,即,时取等号.
故选B
]
(多选)现有以下结论:
(1)函数的最小值是2; (2)若且,则;
(3)的最小值是2; (4)函数的最小值为
其中,不正确的是( [endnoteRef:11] )
A.(1) B.(2) C.(3) D.(4) [11: 答案:ACD;]
桑基鱼塘是广东省珠江三角洲一种独具地方特色的农业生产形式,某研究单位打算开发一个桑基鱼塘项目,该项目准备购置一块1 800平方米的矩形地块,中间挖成三个矩形池塘养鱼,挖出的泥土堆在池塘四周形成基围(阴影部分所示)种植桑树,鱼塘周围的基围宽均为2米,如图所示,池塘所占面积为S平方米,其中.
(1)试用x,y表示S;
(2)若要使S最大,则x,y的值各为多少?([endnoteRef:12])
[12: 解析:(1)由题可得,xy=1 800,b=2a,则y=a+b+6=3a+6,
S=(x-4)a+(x-6)b=(3x-16)a=(3x-16)=1 832-6x-y(x>6,y>6,xy=1 800).
(2)方法一 S=1 832-6x-y≤1 832-2=1 832-480=1 352,
当且仅当6x=y,xy=1 800,即x=40,y=45时,S取得最大值1 352.
方法二 S=1 832-6x-×=1 832-≤1 832-2=1 832-480=1 352,
当且仅当6x=,即x=40时取等号,S取得最大值,此时y==45.
]
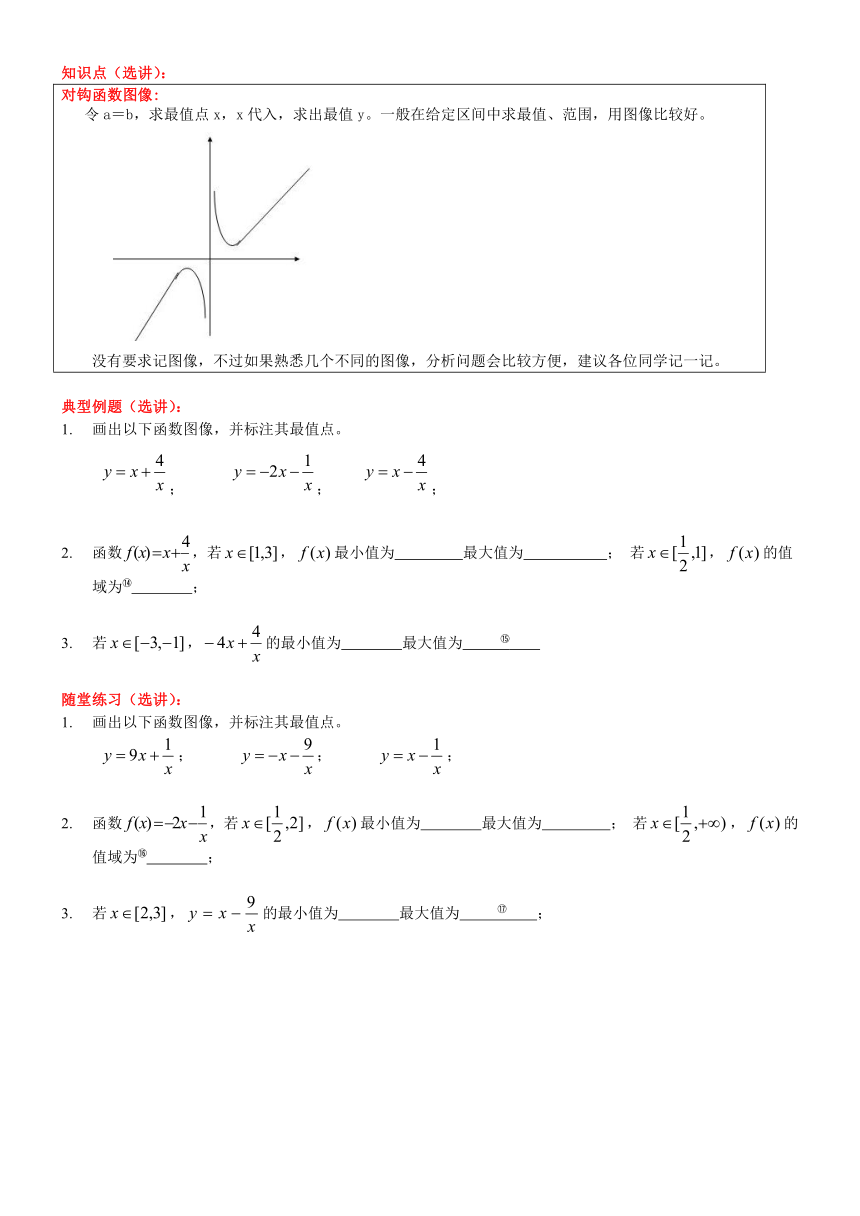
知识点(选讲):
对钩函数图像: 令a=b,求最值点x,x代入,求出最值y。一般在给定区间中求最值、范围,用图像比较好。 没有要求记图像,不过如果熟悉几个不同的图像,分析问题会比较方便,建议各位同学记一记。
典型例题(选讲):
画出以下函数图像,并标注其最值点。
; ; ;
函数,若,最小值为 最大值为 ; 若,的值域为[endnoteRef:13] ; [13: 答案:4,5,;]
若,的最小值为 最大值为 [endnoteRef:14] [14: 答案:0,;]
随堂练习(选讲):
画出以下函数图像,并标注其最值点。
; ; ;
函数,若,最小值为 最大值为 ; 若,的值域为[endnoteRef:15] ; [15: 答案:,,;]
若,的最小值为 最大值为 [endnoteRef:16] ; [16: 答案:,0;]
《不等式》专题6-2 基本不等式最值分析(中下)
已知非负实数a,b满足2a+3b=10,则最大值是( [endnoteRef:17] )
A. B. C.5 D.10 [17: 答案:B;]
(1)若x<3,求y=2x+1+的最大值;
(2)已知x>0,求y=的最大值.([endnoteRef:18]) [18: 解:(1)因为x<3,所以3-x>0.又因为y=2(x-3)++7=-+7,由基本不等式可得2(3-x)+≥2=2,当且仅当2(3-x)=,即x=3-时,等号成立,于是-≤-2,-+7≤7-2,故y的最大值是7-2.
(2)y==.因为x>0,所以x+≥2=2,所以0<y≤=1,当且仅当x=,即x=1时,等号成立.故y的最大值为1.
]
函数的值域是( [endnoteRef:19] )
A. B C或 D [19: 答案:C;]
若,的最大值为 [endnoteRef:20] [20: 答案:;]
已知x≥,则y=有([endnoteRef:21] )
A.最大值 B.最小值 C.最大值1 D.最小值1 [21: D 解析:y===,
因为x≥,所以x-2>0,所以≥·2=1,
当且仅当x-2=,即x=3时取等号.故y的最小值为1.]
(多选)设a>0,b>0,a+2b=1,则([endnoteRef:22] )
A.ab的最大值为 B.的最小值为
C.的最小值为8 D.的最小值为 [22: 答案:ABD;]
已知,且,则下列不等式
①;②;③;④。
其中正确的序号是____[endnoteRef:23]___.
[23: 答案:①②③;]
已知a>0,b>0,+=,若不等式2a+b≥9m恒成立,则m的最大值为([endnoteRef:24] )
A.8 B.7 C.6 D.5 [24: C 解析:可得6=1,所以2a+b=6·(2a+b)=6≥6×(5+4)=54,当且仅当=时等号成立,所以9m≤54,即m≤6,故选C.]
(填空3)若a,b均为非负数且a+b=1, 则的最小值为[endnoteRef:25]______.
[25: 答案:3;]
某游泳馆出售冬季游泳卡,每张240元,其使用规定:不记名,每卡每次只限一人,每天只限一次.某班有48名同学,老师打算组织同学们集体去游泳,除需购买若干张游泳卡外,每次游泳还需包一辆汽车,无论乘坐多少名同学,每次的包车费均为40元.若使每名同学游8次,每人最少应交多少元钱?([endnoteRef:26]) [26: 解 设买x张游泳卡,总开支为y元,则每批去x名同学,共需去批,总开支又分为:①买卡所需费用240x,②包车所需费用×40.
∴y=240x+×40(0∴y=240≥240×2=3840,
当且仅当x=,即x=8时取等号.故每人最少应交=80(元).
]
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过C点,已知|AB|=3 m,|AD|=2 m.
(1)要使矩形AMPN的面积大于32 m2,则AN的长度应在什么范围内?
(2)当AN的长度是多少时,矩形AMPN的面积最小?并求出最小值.[endnoteRef:27]
[27: 答案:;
解 设AN的长为x m(x>2),则由=得|AM|=.所以S矩形AMPN=|AN|·|AM|=.
(1)由S矩形AMPN>32,得>32.又x>2,所以3x2-32x+64>0,解得28.所以AN的长度的取值范围为∪(8,+∞).
(2)因为S矩形AMPN===3(x-2)++12≥2+12=24,当且仅当3(x-2)=,即x=4时,等号成立.
所以当AN的长度是4 m时,矩形AMPN的面积最小,最小值为24 m2.]
(选做)函数,若,最小值为 最大值为 ;若,的值域为[endnoteRef:28] ; [28: 答案:2,,;]
(选做)若,的最小值为 最大值为 [endnoteRef:29] ; [29: 答案:-3,0;]
《不等式》专题6-3 基本不等式最值分析(中下)
(-6≤a≤3)的最大值为([endnoteRef:30] )
A.9 B. C.3 D. [30: B 解析:选B.因为-6≤a≤3,所以3-a≥0,a+6≥0,
所以≤=.即(-6≤a≤3)的最大值为.
]
当时,的最大值为[endnoteRef:31]________,此时x=______. [31: 【答案】-3,-2;
【解析】当时,
又,,故答案为:-3
]
已知,,,且,,则的最小值是( [endnoteRef:32] )
A.3 B.4 C.5 D.6 [32: 【答案】B
【解析】
由知,,,
,
当且仅当时取等号.
故的最小值为4
故选:B
]
若,函数的最大值为 [endnoteRef:33] [33: 答案:;]
若,则的最大值为( [endnoteRef:34] )
A. B. C. D.1 [34: 答案:C;
解:
∵ ∴
从而,.即。]
(多选)设正实数满足,则下列说法正确的是( [endnoteRef:35] )
A.的最小值为4 B.的最大值为
C.的最小值为 D.的最小值为 [35: 答案:ABD;]
(多选)设,,给出下列不等式恒成立的是( [endnoteRef:36] ).
A. B. C. D. [36: 【答案】ACD
【解析】
设,,
,成立,
,不成立
,当且仅当即时取等号,故成立,
,,,当且仅当,即时取等号,故成立,
故选:.
]
已知,,若不等式恒成立,则的最大值为______[endnoteRef:37]. [37: 【答案】9.
【解析】由得恒成立,而,故,所以的最大值为.
]
已知,不等式恒成立,则的取值范围是 [endnoteRef:38] .
(答案写成集合或区间格式) [38: 答案:;]
某产品原来的成本为1000元/件,售价为1200元/件,年销售量为1万件,由于市场饱和,顾客要求提高,公司计划投入资金进行产品升级.据市场调查,若投入x万元,每件产品的成本将降低元,在售价不变的情况下,年销售量将减少万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为z(单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
(1)求z的函数解析式;
(2)求z的最大值,以及z取得最大值时x的值.([endnoteRef:39]) [39: 解 (1)依题意,产品升级后,每件产品的成本为元,每件产品的利润为元,年销售量为万件,
故z=-x=198.5--.
(2)z=198.5--≤198.5-2× =178.5,
当且仅当=,即x=40时取到等号,即z的最大值是178.5,当z取得最大值时x的值为40.
]
围建一个360 m2的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为2 m的进出口,如图所示.已知旧墙的维修费用为45元/m,新墙的造价为180元/m.设利用的旧墙长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元).
(1)将y表示为x的函数;
(2)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.[endnoteRef:40] [40: 答案:;
解 (1)如图,设矩形的另一边长为a m,
则y=45x+180(x-2)+180·2a=225x+360a-360,
由已知xa=360,得a=.
∴y=225x+-360(x>0).
(2)∵x>0,∴225x+≥2=10800.
∴y=225x+-360≥10440.当且仅当225x=时,等号成立.
即当x=24 m时,修建围墙的总费用最小,最小总费用是10440元.
]
(选做)函数,若,最小值为 最大值为 ; 若,的值域为[endnoteRef:41] ; [41: 答案:-10,-6,;]
(选做)若,的最小值为 最大值为 [endnoteRef:42] ; [42: 答案:,-1;]
《不等式》专题6-4 基本不等式最值分析(中下)
若实数,满足,则的最小值为[endnoteRef:43]______. [43: 【答案】4
【解析】因为,
所以,当时取“”,
所以的最小值为4,故答案为4.
]
求下列函数的最值
(1)已知x<,求f(x)=4x-2+的最大值.([endnoteRef:44]) [44: 解析:因为x<,所以4x-5<0,5-4x>0.
f(x)=4x-5+3+=-+3
≤-2+3=1.
当且仅当5-4x=时等号成立,
又5-4x>0,
所以5-4x=1,x=1.
所以f(x)max=f(1)=1.
]
函数的值域是[endnoteRef:45] 。 [45: 答案:;
提示:;
所以函数的值域是。]
若对任意,恒成立,则的取值范围是 [endnoteRef:46] .
[46: 答案:;
【解析】因为,所以(当且仅当时取等号),所以有
,即的最大值为,故.
]
函数y=的最小值为( [endnoteRef:47] )
A.2 B. C.1 D.不存在 [47: 答案:B;
解析 y==+
∵≥2,而≤,所以不能用基本不等式求最小值,用函数的单调性求最值,函数y=x+在(1,+∞)上是增函数,∴在[2,+∞)上也是增函数.
∴当=2即x=0时,ymin=.
]
(多选)设,,,则([endnoteRef:48] )
A.ab的最大值为 B.的最小值为
C.的最小值为8 D.的最小值为 [48: 答案:ABD;
【解析】,得,当且,时取等号,故A正确;
,当且仅当,时取等号,故B正确;
,当且仅当时取等号,故C错误;
,当且仅当,时取等号,故D正确,
故选ABD.
]
给出下列结论:
①若a>0,则a2+1>a. ①若a>0,b>0,则≥4.
③若a>0,b>0,则(a+b)≥4. ④若a∈R且a≠0,则+a≥6.
其中恒成立的是[endnoteRef:49]________. [49: 答案:①②③;
[解析] 因为(a2+1)-a=2+>0,所以a2+1>a,故①恒成立.
因为a>0,所以a+≥2,因为b>0,所以b+≥2,所以当a>0,b>0时,≥4,故②恒成立.
因为(a+b)=2++,又因为a,b∈(0,+∞),所以+≥2,所以(a+b)≥4,故③恒成立.
因为a∈R且a≠0,不符合基本不等式的条件,故+a≥6是错误的.]
已知且,求使不等式恒成立的实数m的取值范围.([endnoteRef:50]) [50: 【答案】.
【解析】
由,则.
当且仅当即时取到最小值16.
若恒成立,则.
]
函数y=loga(x+3)-1 (a>0,a≠1)的图象恒过点A,若点A在直线mx+ny+1=0上,其中mn>0,
则+的最小值为_____[endnoteRef:51]___. [51: 答案:8;
解析 ∵A(-2,-1)在直线mx+ny+1=0上,
∴-2m-n+1=0,
即2m+n=1,mn>0,∴m>0,n>0.
∴+=+=2+++2≥4+2·=8.
当且仅当=,即m=,n=时等号成立.
故+的最小值为8.
]
近年来,中美贸易摩擦不断.特别是美国对我国华为的限制.尽管美国对华为极力封锁,百般刁难,并不断加大对各国的施压,拉拢他们抵制华为5G,然而这并没有让华为却步.华为在2018年不仅净利润创下记录,海外增长同样强劲.今年,我国华为某一企业为了进一步增加市场竞争力,计划在2020年利用新技术生产某款新手机.通过市场分析,生产此款手机全年需投入固定成本250万,每生产(千部)手机,需另投入成本万元,且 ,由市场调研知,每部手机售价0.7万元,且全年内生产的手机当年能全部销售完.
(I)求出2020年的利润(万元)关于年产量(千部)的函数关系式,(利润=销售额—成本);
2020年产量为多少(千部)时,企业所获利润最大?最大利润是多少?([endnoteRef:52]) [52: 【答案】(Ⅰ)(Ⅱ)2020年产量为100(千部)时,企业所获利润最大,最大利润是9000万元.
【解析】(Ⅰ)当时,;
当时,,
.
(Ⅱ)若,,
当时,万元 .
若,,
当且仅当时,即时,万元 .
2020年产量为100(千部)时,企业所获利润最大,最大利润是9000万元.
]
某商场[endnoteRef:53]的某种商品的年进货量为1万件,分若干次进货,每次进货的量相同,且需运费100元,运来的货物除出售外,还需租仓库存放,一年的租金按一次进货时的一半来计算,每件2元,为使一年的运费和租金最省,求每次进货量应多少 [53: 答案:D;
解析:设每次进x件,费用为y元,由=2000,
仅当 时最小。
]
(选做)函数,若,最小值为 最大值为 ; 若,的值域为[endnoteRef:54] ; [54: 答案:6,,;]
(选做)若,的最小值为 最大值为 [endnoteRef:55] ; [55: 答案:8,;]
《不等式》专题6-5 基本不等式最值分析(中下)
若0<x<,则函数y=x的最大值为([endnoteRef:56] )
A.1 B. C. D. [56: C解析:因为0<x<,所以1-4x2>0,所以x=×2x≤×=,当且仅当2x=,即x=时等号成立,故选C.]
若a<1,则a+有最______值,为____[endnoteRef:57]____.(中下,凑数) [57: 答案:大 -1;
解析 ∵a<1,∴a-1<0,
∴-=(1-a)+≥2(a=0时取等号),
∴a-1+≤-2,∴a+≤-1.
]
当,关于代数式,下列说法正确的是 [endnoteRef:58]
A.有最大值无最小值 B.有最小值无最大值
C.有最小值也有最大值 D.无最小值也无最大值 [58: 【答案】A
【解析】,,当且仅当即时取等号,
故,关于代数式有最大值1,没有最小值,故选:A.
]
若,的最大值为 [endnoteRef:59] [59: 答案:;]
设x>-1,则函数y=的最小值是___[endnoteRef:60]_____.
[60: 答案:9;
解析 ∵x>-1,∴x+1>0,
设x+1=t>0,则x=t-1,
于是有y===t++5≥2+5=9,
当且仅当t=,即t=2时取等号,此时x=1.
∴当x=1时,
函数y=取得最小值为9.
]
(多选)设x,,,,以下四个命题中正确的是([endnoteRef:61] )
A.若,则S有最小值2 B.若,则S有最小值4
C.若,则有最小值2 D.若,则P有最大值1 [61: 答案:AD;
解:,即
,当且仅当时取“=”,A正确
,即,即
当且仅当,即时取“=”,最小值为2,B错
若,当且仅当即即时取“=”
此时矛盾,C错
∴最小值不能是2.
,∴
,∴
即,当且仅当时取“=”,D正确
选AD]
(多选)下列选项正确的是( [endnoteRef:62] )
A.若,则的最小值为4; B.若,则的最小值为2;
C.若,则的最大值为-2; D.若正实数x,y满足,则的最小值为8 [62: 答案:CD;]
若,且,恒成立,则实数的取值范围是([endnoteRef:63] )
A. B. C. D. [63: 【答案】A
【解析】由基本不等式得,
当且仅当,即当时,等号成立,所以,的最小值为.
由题意可得,即,解得或.
因此,实数的取值范围是,故选:B.
]
已知:是正常数,,且的最小值为18,求的值. ([endnoteRef:64]) [64: 答案:; ]
已知A、B两地的距离是100km,按交通法规定,A、B两地之间的公路车速x应限制在60~120km/h,假设汽油的价格是7元/L,汽车的耗油率为,司机每小时的工资是70元(设汽车为匀速行驶),那么最经济的车速是多少?如果不考虑其他费用,这次行车的总费用是多少?([endnoteRef:65]) [65: 【答案】80,280
【解析】设总费用为
则
当时等号成立,满足条件
故最经济的车速是,总费用为280.
]
某厂家[endnoteRef:66]拟在2008年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)x万件与年促销费用m万元()(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件。已知2005年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2008年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2008年的促销费用投入多少万元时,厂家的利润最大? [66: 答案:;
解(1)由题意可知当
每件产品的销售价格为,
∴2008年的利润
.
(2),
(万元)
答:该厂家2008年的促销费用投入3万元时,厂家的利润最大.
]
(选做)函数,若,最小值为 最大值为 ; 若,的值域为 ;[endnoteRef:67] [67: 答案:3,,;]
(选做)若,的最小值为 最大值为 [endnoteRef:68] [68: 答案:,;]
《不等式》专题6-6 基本不等式最值分析(中下)
设为实数,若则的最大值是 [endnoteRef:69] 。
[69: 答案:;]
已知x<3,则的最大值是[endnoteRef:70]______. [70: 答案:-1;]
函数的值域为[endnoteRef:71] . [71: 答案:;]
若,的最大值为 [endnoteRef:72] [72: 答案:;]
已知关于的不等式在上恒成立,求实数的最小值;([endnoteRef:73]) [73: 答案:3;
]
(多选)下列结论不正确的是([endnoteRef:74] )
A.当x>0时, B.当x>0时,的最小值是2
C.当时,的最小值是 D.设x>0,y>0,且x+y=2,则的最小值是 [74: 答案:BC;]
(多选)下列结论不正确的是( [endnoteRef:75] )
A.; B.; C.; D. [75: 答案:ACD;]
求下列函数的最值
(2)已知x∈,求函数y=+的最小值.([endnoteRef:76]) [76: (2)解析:y=+=·(2x+1-2x)=10+2·+8·,
而x∈,2·+8·≥2=8,
当且仅当2·=8·,
即x=∈时取到等号,则y≥18,
所以函数y=+的最小值为18.]
已知,,不等式恒成立,则的取值范围是 [endnoteRef:77] .
(答案写成集合或区间格式) [77: 答案:;]
(多选)若正实数a,b满足则下列说法正确的是( [endnoteRef:78] )
A.ab有最大值 B.有最大值
C.有最小值2 D.有最大值 [78: 【答案】AB
【解析】
对A,,当且仅当时取等号.故A正确.
对B, ,故,当且仅当时取等号.故B正确.
对C, .当且仅当时取等号.所以有最小值4.故C错误.
对D, ,即,故有最小值.故D错误.
故选:AB
]
某单位修建一个长方形无盖蓄水池,其容积为1875立方米,深度为3米,池底每平方米的造价为100元,池壁每平方米的造价为120元,设池底长方形的长为米.
(1)用含的表达式表示池壁面积;
(2)当为多少米时,水池的总造价最低,最低造价是多少?([endnoteRef:79]) [79: 【答案】(1);(2)当米时,最低造价是元.
【解析】(1)由题意得:池底面积为平方米,池底长方形的宽为米
(2)设总造价为元,则:
化简得:
因为,当且仅当,即时取等号
即当米时,最低造价是元
]
经过[endnoteRef:80]长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度v(千米/小时)之间的函数关系为:。
(1)在该时段内,当汽车的平均速度v为多少时,车流量最大?最大车流量为多少?(精确到0.1千辆/小时)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车站的平均速度应在什么范围内? [80: 答案:;
]
(选做)函数,若,最小值为 最大值为 ; 若,的值域为[endnoteRef:81] ; [81: 答案:10,,;]
(选做)若,的最小值为 最大值为 [endnoteRef:82] ; [82: 答案:0,;]
(6套13页)
典型例题:
若,且,则:([endnoteRef:0])
(1)的最大值为 ;(2)的最大值为 ;(3)的最大值为 ; [0: 答案:6,,12;]
不等式a2+1≥2a中等号成立的条件是([endnoteRef:1] )
A.a=±1 B.a=1 C.a=-1 D.a=0 [1: 答案:B;
[解析] a2+1-2a=(a-1)2≥0,∴a=1时,等号成立.]
若a<1,则a+与-1的大小关系是[endnoteRef:2]________. [2: 答案:a+≤-1;
解析:因为a<1,即1-a>0,所以-=(1-a)+≥2 =2.
即a+≤-1.]
若,的最大值为 [endnoteRef:3] [3: 答案:;]
(多选)设正实数,满足,则([endnoteRef:4] )
A.有最小值4 B.有最小值
C.有最大值1 D.有最小值 [4: 答案:AD;]
(多选)已知a,b>0且2a+b=1,则的值不可能是( [endnoteRef:5] )
A.7 B.8 C.9 D.10 [5: 答案:ABD;]
已知,则的最大值为 [endnoteRef:6] . [6: 答案:6;]
随堂练习:
若正实数a,b满足,则下列说法正确的是 [endnoteRef:7]
A.ab有最小值 B.有最小值
C.有最小值4 D.有最小值 [7: 【答案】C
【解析】,,且;;
;有最大值,选项A错误;
,,即有最大值,B项错误.
,有最小值4,C正确;
,的最小值是,不是,D错误.
]
已知a
由基本不等式可得+b-a=1++(b-a)≥1+2=3,
当且仅当=b-a(b>a),即当b-a=1时,等号成立,因此,+b-a的最小值为3,故选A.]
已知不等式(x+y)≥9对任意x、y为正实数恒成立,则正数a的最小值为____[endnoteRef:9]____.
[9: 答案:4;
[解析] 展开后,利用基本不等式,而后解不等式可求a值.
∵(x+y)=1+++a≥a+1+2(a>0),∴要使原不等式恒成立,则只需a+1+2≥9,即(-2)(+4)≥0,故≥2,即a≥4,∴正数a的最小值是4.
]
(2020·浙江鄞州·宁波华茂外国语学校高三一模)已知实数,,,则的最小值是( [endnoteRef:10] ) A. B. C. D. [10: 【答案】B
【解析】
∵,,
∴
当且仅当,即,时取等号.
故选B
]
(多选)现有以下结论:
(1)函数的最小值是2; (2)若且,则;
(3)的最小值是2; (4)函数的最小值为
其中,不正确的是( [endnoteRef:11] )
A.(1) B.(2) C.(3) D.(4) [11: 答案:ACD;]
桑基鱼塘是广东省珠江三角洲一种独具地方特色的农业生产形式,某研究单位打算开发一个桑基鱼塘项目,该项目准备购置一块1 800平方米的矩形地块,中间挖成三个矩形池塘养鱼,挖出的泥土堆在池塘四周形成基围(阴影部分所示)种植桑树,鱼塘周围的基围宽均为2米,如图所示,池塘所占面积为S平方米,其中.
(1)试用x,y表示S;
(2)若要使S最大,则x,y的值各为多少?([endnoteRef:12])
[12: 解析:(1)由题可得,xy=1 800,b=2a,则y=a+b+6=3a+6,
S=(x-4)a+(x-6)b=(3x-16)a=(3x-16)=1 832-6x-y(x>6,y>6,xy=1 800).
(2)方法一 S=1 832-6x-y≤1 832-2=1 832-480=1 352,
当且仅当6x=y,xy=1 800,即x=40,y=45时,S取得最大值1 352.
方法二 S=1 832-6x-×=1 832-≤1 832-2=1 832-480=1 352,
当且仅当6x=,即x=40时取等号,S取得最大值,此时y==45.
]
知识点(选讲):
对钩函数图像: 令a=b,求最值点x,x代入,求出最值y。一般在给定区间中求最值、范围,用图像比较好。 没有要求记图像,不过如果熟悉几个不同的图像,分析问题会比较方便,建议各位同学记一记。
典型例题(选讲):
画出以下函数图像,并标注其最值点。
; ; ;
函数,若,最小值为 最大值为 ; 若,的值域为[endnoteRef:13] ; [13: 答案:4,5,;]
若,的最小值为 最大值为 [endnoteRef:14] [14: 答案:0,;]
随堂练习(选讲):
画出以下函数图像,并标注其最值点。
; ; ;
函数,若,最小值为 最大值为 ; 若,的值域为[endnoteRef:15] ; [15: 答案:,,;]
若,的最小值为 最大值为 [endnoteRef:16] ; [16: 答案:,0;]
《不等式》专题6-2 基本不等式最值分析(中下)
已知非负实数a,b满足2a+3b=10,则最大值是( [endnoteRef:17] )
A. B. C.5 D.10 [17: 答案:B;]
(1)若x<3,求y=2x+1+的最大值;
(2)已知x>0,求y=的最大值.([endnoteRef:18]) [18: 解:(1)因为x<3,所以3-x>0.又因为y=2(x-3)++7=-+7,由基本不等式可得2(3-x)+≥2=2,当且仅当2(3-x)=,即x=3-时,等号成立,于是-≤-2,-+7≤7-2,故y的最大值是7-2.
(2)y==.因为x>0,所以x+≥2=2,所以0<y≤=1,当且仅当x=,即x=1时,等号成立.故y的最大值为1.
]
函数的值域是( [endnoteRef:19] )
A. B C或 D [19: 答案:C;]
若,的最大值为 [endnoteRef:20] [20: 答案:;]
已知x≥,则y=有([endnoteRef:21] )
A.最大值 B.最小值 C.最大值1 D.最小值1 [21: D 解析:y===,
因为x≥,所以x-2>0,所以≥·2=1,
当且仅当x-2=,即x=3时取等号.故y的最小值为1.]
(多选)设a>0,b>0,a+2b=1,则([endnoteRef:22] )
A.ab的最大值为 B.的最小值为
C.的最小值为8 D.的最小值为 [22: 答案:ABD;]
已知,且,则下列不等式
①;②;③;④。
其中正确的序号是____[endnoteRef:23]___.
[23: 答案:①②③;]
已知a>0,b>0,+=,若不等式2a+b≥9m恒成立,则m的最大值为([endnoteRef:24] )
A.8 B.7 C.6 D.5 [24: C 解析:可得6=1,所以2a+b=6·(2a+b)=6≥6×(5+4)=54,当且仅当=时等号成立,所以9m≤54,即m≤6,故选C.]
(填空3)若a,b均为非负数且a+b=1, 则的最小值为[endnoteRef:25]______.
[25: 答案:3;]
某游泳馆出售冬季游泳卡,每张240元,其使用规定:不记名,每卡每次只限一人,每天只限一次.某班有48名同学,老师打算组织同学们集体去游泳,除需购买若干张游泳卡外,每次游泳还需包一辆汽车,无论乘坐多少名同学,每次的包车费均为40元.若使每名同学游8次,每人最少应交多少元钱?([endnoteRef:26]) [26: 解 设买x张游泳卡,总开支为y元,则每批去x名同学,共需去批,总开支又分为:①买卡所需费用240x,②包车所需费用×40.
∴y=240x+×40(0
当且仅当x=,即x=8时取等号.故每人最少应交=80(元).
]
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过C点,已知|AB|=3 m,|AD|=2 m.
(1)要使矩形AMPN的面积大于32 m2,则AN的长度应在什么范围内?
(2)当AN的长度是多少时,矩形AMPN的面积最小?并求出最小值.[endnoteRef:27]
[27: 答案:;
解 设AN的长为x m(x>2),则由=得|AM|=.所以S矩形AMPN=|AN|·|AM|=.
(1)由S矩形AMPN>32,得>32.又x>2,所以3x2-32x+64>0,解得2
(2)因为S矩形AMPN===3(x-2)++12≥2+12=24,当且仅当3(x-2)=,即x=4时,等号成立.
所以当AN的长度是4 m时,矩形AMPN的面积最小,最小值为24 m2.]
(选做)函数,若,最小值为 最大值为 ;若,的值域为[endnoteRef:28] ; [28: 答案:2,,;]
(选做)若,的最小值为 最大值为 [endnoteRef:29] ; [29: 答案:-3,0;]
《不等式》专题6-3 基本不等式最值分析(中下)
(-6≤a≤3)的最大值为([endnoteRef:30] )
A.9 B. C.3 D. [30: B 解析:选B.因为-6≤a≤3,所以3-a≥0,a+6≥0,
所以≤=.即(-6≤a≤3)的最大值为.
]
当时,的最大值为[endnoteRef:31]________,此时x=______. [31: 【答案】-3,-2;
【解析】当时,
又,,故答案为:-3
]
已知,,,且,,则的最小值是( [endnoteRef:32] )
A.3 B.4 C.5 D.6 [32: 【答案】B
【解析】
由知,,,
,
当且仅当时取等号.
故的最小值为4
故选:B
]
若,函数的最大值为 [endnoteRef:33] [33: 答案:;]
若,则的最大值为( [endnoteRef:34] )
A. B. C. D.1 [34: 答案:C;
解:
∵ ∴
从而,.即。]
(多选)设正实数满足,则下列说法正确的是( [endnoteRef:35] )
A.的最小值为4 B.的最大值为
C.的最小值为 D.的最小值为 [35: 答案:ABD;]
(多选)设,,给出下列不等式恒成立的是( [endnoteRef:36] ).
A. B. C. D. [36: 【答案】ACD
【解析】
设,,
,成立,
,不成立
,当且仅当即时取等号,故成立,
,,,当且仅当,即时取等号,故成立,
故选:.
]
已知,,若不等式恒成立,则的最大值为______[endnoteRef:37]. [37: 【答案】9.
【解析】由得恒成立,而,故,所以的最大值为.
]
已知,不等式恒成立,则的取值范围是 [endnoteRef:38] .
(答案写成集合或区间格式) [38: 答案:;]
某产品原来的成本为1000元/件,售价为1200元/件,年销售量为1万件,由于市场饱和,顾客要求提高,公司计划投入资金进行产品升级.据市场调查,若投入x万元,每件产品的成本将降低元,在售价不变的情况下,年销售量将减少万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为z(单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
(1)求z的函数解析式;
(2)求z的最大值,以及z取得最大值时x的值.([endnoteRef:39]) [39: 解 (1)依题意,产品升级后,每件产品的成本为元,每件产品的利润为元,年销售量为万件,
故z=-x=198.5--.
(2)z=198.5--≤198.5-2× =178.5,
当且仅当=,即x=40时取到等号,即z的最大值是178.5,当z取得最大值时x的值为40.
]
围建一个360 m2的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为2 m的进出口,如图所示.已知旧墙的维修费用为45元/m,新墙的造价为180元/m.设利用的旧墙长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元).
(1)将y表示为x的函数;
(2)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.[endnoteRef:40] [40: 答案:;
解 (1)如图,设矩形的另一边长为a m,
则y=45x+180(x-2)+180·2a=225x+360a-360,
由已知xa=360,得a=.
∴y=225x+-360(x>0).
(2)∵x>0,∴225x+≥2=10800.
∴y=225x+-360≥10440.当且仅当225x=时,等号成立.
即当x=24 m时,修建围墙的总费用最小,最小总费用是10440元.
]
(选做)函数,若,最小值为 最大值为 ; 若,的值域为[endnoteRef:41] ; [41: 答案:-10,-6,;]
(选做)若,的最小值为 最大值为 [endnoteRef:42] ; [42: 答案:,-1;]
《不等式》专题6-4 基本不等式最值分析(中下)
若实数,满足,则的最小值为[endnoteRef:43]______. [43: 【答案】4
【解析】因为,
所以,当时取“”,
所以的最小值为4,故答案为4.
]
求下列函数的最值
(1)已知x<,求f(x)=4x-2+的最大值.([endnoteRef:44]) [44: 解析:因为x<,所以4x-5<0,5-4x>0.
f(x)=4x-5+3+=-+3
≤-2+3=1.
当且仅当5-4x=时等号成立,
又5-4x>0,
所以5-4x=1,x=1.
所以f(x)max=f(1)=1.
]
函数的值域是[endnoteRef:45] 。 [45: 答案:;
提示:;
所以函数的值域是。]
若对任意,恒成立,则的取值范围是 [endnoteRef:46] .
[46: 答案:;
【解析】因为,所以(当且仅当时取等号),所以有
,即的最大值为,故.
]
函数y=的最小值为( [endnoteRef:47] )
A.2 B. C.1 D.不存在 [47: 答案:B;
解析 y==+
∵≥2,而≤,所以不能用基本不等式求最小值,用函数的单调性求最值,函数y=x+在(1,+∞)上是增函数,∴在[2,+∞)上也是增函数.
∴当=2即x=0时,ymin=.
]
(多选)设,,,则([endnoteRef:48] )
A.ab的最大值为 B.的最小值为
C.的最小值为8 D.的最小值为 [48: 答案:ABD;
【解析】,得,当且,时取等号,故A正确;
,当且仅当,时取等号,故B正确;
,当且仅当时取等号,故C错误;
,当且仅当,时取等号,故D正确,
故选ABD.
]
给出下列结论:
①若a>0,则a2+1>a. ①若a>0,b>0,则≥4.
③若a>0,b>0,则(a+b)≥4. ④若a∈R且a≠0,则+a≥6.
其中恒成立的是[endnoteRef:49]________. [49: 答案:①②③;
[解析] 因为(a2+1)-a=2+>0,所以a2+1>a,故①恒成立.
因为a>0,所以a+≥2,因为b>0,所以b+≥2,所以当a>0,b>0时,≥4,故②恒成立.
因为(a+b)=2++,又因为a,b∈(0,+∞),所以+≥2,所以(a+b)≥4,故③恒成立.
因为a∈R且a≠0,不符合基本不等式的条件,故+a≥6是错误的.]
已知且,求使不等式恒成立的实数m的取值范围.([endnoteRef:50]) [50: 【答案】.
【解析】
由,则.
当且仅当即时取到最小值16.
若恒成立,则.
]
函数y=loga(x+3)-1 (a>0,a≠1)的图象恒过点A,若点A在直线mx+ny+1=0上,其中mn>0,
则+的最小值为_____[endnoteRef:51]___. [51: 答案:8;
解析 ∵A(-2,-1)在直线mx+ny+1=0上,
∴-2m-n+1=0,
即2m+n=1,mn>0,∴m>0,n>0.
∴+=+=2+++2≥4+2·=8.
当且仅当=,即m=,n=时等号成立.
故+的最小值为8.
]
近年来,中美贸易摩擦不断.特别是美国对我国华为的限制.尽管美国对华为极力封锁,百般刁难,并不断加大对各国的施压,拉拢他们抵制华为5G,然而这并没有让华为却步.华为在2018年不仅净利润创下记录,海外增长同样强劲.今年,我国华为某一企业为了进一步增加市场竞争力,计划在2020年利用新技术生产某款新手机.通过市场分析,生产此款手机全年需投入固定成本250万,每生产(千部)手机,需另投入成本万元,且 ,由市场调研知,每部手机售价0.7万元,且全年内生产的手机当年能全部销售完.
(I)求出2020年的利润(万元)关于年产量(千部)的函数关系式,(利润=销售额—成本);
2020年产量为多少(千部)时,企业所获利润最大?最大利润是多少?([endnoteRef:52]) [52: 【答案】(Ⅰ)(Ⅱ)2020年产量为100(千部)时,企业所获利润最大,最大利润是9000万元.
【解析】(Ⅰ)当时,;
当时,,
.
(Ⅱ)若,,
当时,万元 .
若,,
当且仅当时,即时,万元 .
2020年产量为100(千部)时,企业所获利润最大,最大利润是9000万元.
]
某商场[endnoteRef:53]的某种商品的年进货量为1万件,分若干次进货,每次进货的量相同,且需运费100元,运来的货物除出售外,还需租仓库存放,一年的租金按一次进货时的一半来计算,每件2元,为使一年的运费和租金最省,求每次进货量应多少 [53: 答案:D;
解析:设每次进x件,费用为y元,由=2000,
仅当 时最小。
]
(选做)函数,若,最小值为 最大值为 ; 若,的值域为[endnoteRef:54] ; [54: 答案:6,,;]
(选做)若,的最小值为 最大值为 [endnoteRef:55] ; [55: 答案:8,;]
《不等式》专题6-5 基本不等式最值分析(中下)
若0<x<,则函数y=x的最大值为([endnoteRef:56] )
A.1 B. C. D. [56: C解析:因为0<x<,所以1-4x2>0,所以x=×2x≤×=,当且仅当2x=,即x=时等号成立,故选C.]
若a<1,则a+有最______值,为____[endnoteRef:57]____.(中下,凑数) [57: 答案:大 -1;
解析 ∵a<1,∴a-1<0,
∴-=(1-a)+≥2(a=0时取等号),
∴a-1+≤-2,∴a+≤-1.
]
当,关于代数式,下列说法正确的是 [endnoteRef:58]
A.有最大值无最小值 B.有最小值无最大值
C.有最小值也有最大值 D.无最小值也无最大值 [58: 【答案】A
【解析】,,当且仅当即时取等号,
故,关于代数式有最大值1,没有最小值,故选:A.
]
若,的最大值为 [endnoteRef:59] [59: 答案:;]
设x>-1,则函数y=的最小值是___[endnoteRef:60]_____.
[60: 答案:9;
解析 ∵x>-1,∴x+1>0,
设x+1=t>0,则x=t-1,
于是有y===t++5≥2+5=9,
当且仅当t=,即t=2时取等号,此时x=1.
∴当x=1时,
函数y=取得最小值为9.
]
(多选)设x,,,,以下四个命题中正确的是([endnoteRef:61] )
A.若,则S有最小值2 B.若,则S有最小值4
C.若,则有最小值2 D.若,则P有最大值1 [61: 答案:AD;
解:,即
,当且仅当时取“=”,A正确
,即,即
当且仅当,即时取“=”,最小值为2,B错
若,当且仅当即即时取“=”
此时矛盾,C错
∴最小值不能是2.
,∴
,∴
即,当且仅当时取“=”,D正确
选AD]
(多选)下列选项正确的是( [endnoteRef:62] )
A.若,则的最小值为4; B.若,则的最小值为2;
C.若,则的最大值为-2; D.若正实数x,y满足,则的最小值为8 [62: 答案:CD;]
若,且,恒成立,则实数的取值范围是([endnoteRef:63] )
A. B. C. D. [63: 【答案】A
【解析】由基本不等式得,
当且仅当,即当时,等号成立,所以,的最小值为.
由题意可得,即,解得或.
因此,实数的取值范围是,故选:B.
]
已知:是正常数,,且的最小值为18,求的值. ([endnoteRef:64]) [64: 答案:; ]
已知A、B两地的距离是100km,按交通法规定,A、B两地之间的公路车速x应限制在60~120km/h,假设汽油的价格是7元/L,汽车的耗油率为,司机每小时的工资是70元(设汽车为匀速行驶),那么最经济的车速是多少?如果不考虑其他费用,这次行车的总费用是多少?([endnoteRef:65]) [65: 【答案】80,280
【解析】设总费用为
则
当时等号成立,满足条件
故最经济的车速是,总费用为280.
]
某厂家[endnoteRef:66]拟在2008年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)x万件与年促销费用m万元()(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件。已知2005年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2008年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2008年的促销费用投入多少万元时,厂家的利润最大? [66: 答案:;
解(1)由题意可知当
每件产品的销售价格为,
∴2008年的利润
.
(2),
(万元)
答:该厂家2008年的促销费用投入3万元时,厂家的利润最大.
]
(选做)函数,若,最小值为 最大值为 ; 若,的值域为 ;[endnoteRef:67] [67: 答案:3,,;]
(选做)若,的最小值为 最大值为 [endnoteRef:68] [68: 答案:,;]
《不等式》专题6-6 基本不等式最值分析(中下)
设为实数,若则的最大值是 [endnoteRef:69] 。
[69: 答案:;]
已知x<3,则的最大值是[endnoteRef:70]______. [70: 答案:-1;]
函数的值域为[endnoteRef:71] . [71: 答案:;]
若,的最大值为 [endnoteRef:72] [72: 答案:;]
已知关于的不等式在上恒成立,求实数的最小值;([endnoteRef:73]) [73: 答案:3;
]
(多选)下列结论不正确的是([endnoteRef:74] )
A.当x>0时, B.当x>0时,的最小值是2
C.当时,的最小值是 D.设x>0,y>0,且x+y=2,则的最小值是 [74: 答案:BC;]
(多选)下列结论不正确的是( [endnoteRef:75] )
A.; B.; C.; D. [75: 答案:ACD;]
求下列函数的最值
(2)已知x∈,求函数y=+的最小值.([endnoteRef:76]) [76: (2)解析:y=+=·(2x+1-2x)=10+2·+8·,
而x∈,2·+8·≥2=8,
当且仅当2·=8·,
即x=∈时取到等号,则y≥18,
所以函数y=+的最小值为18.]
已知,,不等式恒成立,则的取值范围是 [endnoteRef:77] .
(答案写成集合或区间格式) [77: 答案:;]
(多选)若正实数a,b满足则下列说法正确的是( [endnoteRef:78] )
A.ab有最大值 B.有最大值
C.有最小值2 D.有最大值 [78: 【答案】AB
【解析】
对A,,当且仅当时取等号.故A正确.
对B, ,故,当且仅当时取等号.故B正确.
对C, .当且仅当时取等号.所以有最小值4.故C错误.
对D, ,即,故有最小值.故D错误.
故选:AB
]
某单位修建一个长方形无盖蓄水池,其容积为1875立方米,深度为3米,池底每平方米的造价为100元,池壁每平方米的造价为120元,设池底长方形的长为米.
(1)用含的表达式表示池壁面积;
(2)当为多少米时,水池的总造价最低,最低造价是多少?([endnoteRef:79]) [79: 【答案】(1);(2)当米时,最低造价是元.
【解析】(1)由题意得:池底面积为平方米,池底长方形的宽为米
(2)设总造价为元,则:
化简得:
因为,当且仅当,即时取等号
即当米时,最低造价是元
]
经过[endnoteRef:80]长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度v(千米/小时)之间的函数关系为:。
(1)在该时段内,当汽车的平均速度v为多少时,车流量最大?最大车流量为多少?(精确到0.1千辆/小时)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车站的平均速度应在什么范围内? [80: 答案:;
]
(选做)函数,若,最小值为 最大值为 ; 若,的值域为[endnoteRef:81] ; [81: 答案:10,,;]
(选做)若,的最小值为 最大值为 [endnoteRef:82] ; [82: 答案:0,;]
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
