12.2.4 用“HL”证直角三角形全等同步跟踪测试(含答案)
文档属性
| 名称 | 12.2.4 用“HL”证直角三角形全等同步跟踪测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 362.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-26 10:06:45 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
12.2.4 用“HL”证直角三角形全等
一.选择题
1.下列判定两个直角三角形全等的方法中,不正确的是( )
A.两条直角边分别对应相等 B.斜边和一锐角分别对应相等
C.斜边和一条直角边分别对应相等 D.两个三角形的面积相等
2.如图,在四边形ABCD中,AD=CB,DE⊥AC于点E,BF⊥AC于点F,且DE=BF,则图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
2题图 3题图 4题图 5题图
3.如图,已知AB=AD,那么添加下列哪一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
4.如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.AC=AD B.AB=AB C.∠ABC=∠ABD D.∠BAC=∠BAD
5.如图,小敏用三角尺按下面方法画角平分线:在已知的∠AOB的两边上,分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,画射线OP,则OP平分∠AOB,其作图原理是:△OMP≌△ONP,这样就有∠AOP=∠BOP,则说明这两个三角形全等的依据是( )
A.SAS B.ASA C.AAS D.HL
6.如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE与CD相交于O,且∠1=∠2,则下列结论正确的个数为( )
①∠B=∠C;②△ADO≌△AEO;③△BOD≌△COE;④图中有四组三角形全等.
A.1个 B.2个 C.3个 D.4个
6题图 7题图 8题图 9题图 10题图
7.如图,AD⊥DC,AB⊥BC,若AB=AD,∠DAB=120°,则∠ACB的度数为( )
A.30° B.45° C.60° D.75°
8.如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面的两个木桩上,两个木桩离旗杆底部的距离BD与CD间的关系是( )
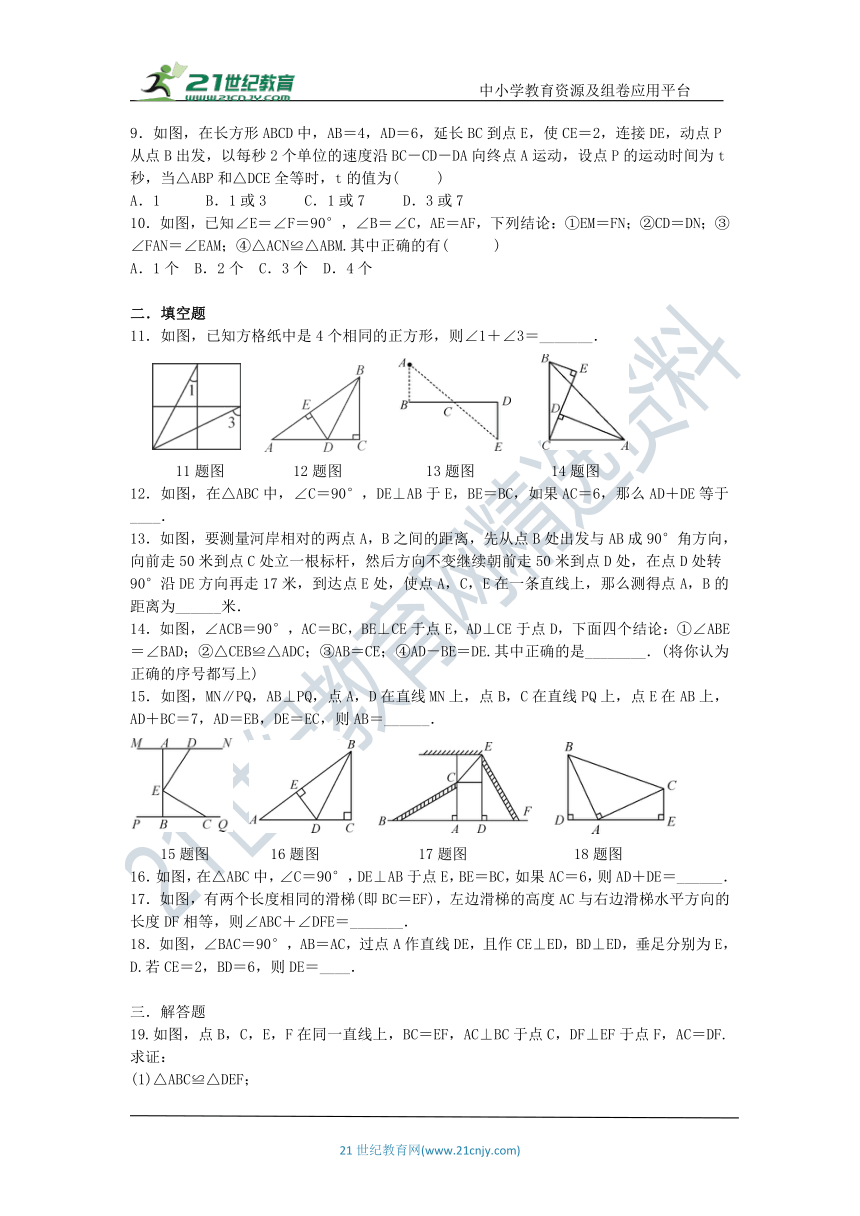
A.BD>CD B.BD9.如图,在长方形ABCD中,AB=4,AD=6,延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当△ABP和△DCE全等时,t的值为( )
A.1 B.1或3 C.1或7 D.3或7
10.如图,已知∠E=∠F=90°,∠B=∠C,AE=AF,下列结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题
11.如图,已知方格纸中是4个相同的正方形,则∠1+∠3=_______.
11题图 12题图 13题图 14题图
12.如图,在△ABC中,∠C=90°,DE⊥AB于E,BE=BC,如果AC=6,那么AD+DE等于____.
13.如图,要测量河岸相对的两点A,B之间的距离,先从点B处出发与AB成90°角方向,向前走50米到点C处立一根标杆,然后方向不变继续朝前走50米到点D处,在点D处转90°沿DE方向再走17米,到达点E处,使点A,C,E在一条直线上,那么测得点A,B的距离为______米.
14.如图,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,下面四个结论:①∠ABE=∠BAD;②△CEB≌△ADC;③AB=CE;④AD-BE=DE.其中正确的是________.(将你认为正确的序号都写上)
15.如图,MN∥PQ,AB⊥PQ,点A,D在直线MN上,点B,C在直线PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB=______.
15题图 16题图 17题图 18题图
16.如图,在△ABC中,∠C=90°,DE⊥AB于点E,BE=BC,如果AC=6,则AD+DE=______.
17.如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=_______.
18.如图,∠BAC=90°,AB=AC,过点A作直线DE,且作CE⊥ED,BD⊥ED,垂足分别为E,D.若CE=2,BD=6,则DE=____.
三.解答题
19.如图,点B,C,E,F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC=DF.求证:
(1)△ABC≌△DEF;
(2)AB∥DE.
20.如图,AD,BC相交于点O,AD=BC,∠C=∠D=90°.
(1)求证:△ACB≌△BDA;
(2)若∠ABC=35°,则∠CAO的度数是多少?
21.已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
(1)如图①,若点O在边BC上,求证:∠ABO=∠ACO;
(2)如图②,若点O在△ABC的内部,求证:∠ABO=∠ACO.
22. 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.求证:DE=AD-BE.
23.如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.(1)图中还有几对全等三角形?请你一一列举;(2)求证:CF=EF.
24.如图,已知A(-2,0),B(0,-4),C(1,1),点P为线段OB上一动点(不包括点O),CD⊥CP交x轴于点D,当P点运动时:
(1)求证:∠CPO=∠CDO;
(2)求证:CP=CD;
(3)下列两个结论:①AD-BP的值不变;②AD+BP的值不变.选择正确的结论并求其值.
参考答案
1-5 DCCAD 6-10DACCC
11.90°
12.6
17
①②④
7
16. 6
17.90°
18. 8
19. 解:(1)∵AC⊥BC于点C,DF⊥EF于点F,∴∠ACB=∠DFE=90°.
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS)
(2)由(1)可知△ABC≌△DEF,∴∠B=∠DEF,
∴AB∥DE
20. 解:(1)∵∠C=∠D=90°,
∴在Rt△ACB和Rt△BDA中
∴Rt△ACB≌Rt△BDA(HL)
(2)∵Rt△ABC≌Rt△BAD,∴∠ABC=∠BAD=35°,
∵∠C=90°,∴∠BAC=55°,
∴∠CAO=∠CAB-∠BAD=20°
21. 解:(1)过点O作OE⊥AB于E,作OF⊥AC于F,
则∠BEO=∠CFO=90°,
又∵OB=OC,OE=OF,∴Rt△BOE≌Rt△COF(HL),
∴∠ABO=∠ACO
(2)过点O分别作OE⊥AB,OF⊥AC,E,F分别是垂足,
则∠BEO=∠CFO=90°,
又∵OB=OC,OE=OF,∴Rt△BOE≌Rt△COF(HL),
∴∠ABO=∠ACO
22. 解:∵BE⊥CE,AD⊥CE,∴∠CEB=∠ADC=90°
又∵∠ACB=90°,∴∠BCE+∠ACD=90°, ∠ACDO+∠CAD=90°
∴∠BCE=∠ACDO
又∵AC=BC
∴△ACD≌△CBE(AAS),
∴AD=CE,BE=CD,
∵DE=CE-CD,∴DE=AD-BE
23. 解:(1)△ADC≌△ABE,△CDF≌△EBF
(2)连接AF,∵Rt△ABC≌Rt△ADE,
∴AB=AD,BC=DE,∠ABC=∠ADE=90°,
又∵AF=AF,∴Rt△ABF≌Rt△ADF(HL),
∴BF=DF,
又∵BC=DE,∴BC-BF=DE-DF,
即CF=EF
24. 解:(1)∵在△POK和△DCK中,∠C=∠POK=90°,∠OKP=∠DKC,
∴∠OPK=∠CDK,即∠CPO=∠CDO
(2)作CM⊥x轴于点M,CN⊥y轴于点N,易证△CMD≌△CNP(AAS),
∴CP=CD
(3)②正确,易证MD=NP,
∵AD=AO+OM+MD=3+MD,BP=NB-NP=NO+OB-NP=5-NP,
∴AD+BP=8
21世纪教育网(www.21cnjy.com)
12.2.4 用“HL”证直角三角形全等
一.选择题
1.下列判定两个直角三角形全等的方法中,不正确的是( )
A.两条直角边分别对应相等 B.斜边和一锐角分别对应相等
C.斜边和一条直角边分别对应相等 D.两个三角形的面积相等
2.如图,在四边形ABCD中,AD=CB,DE⊥AC于点E,BF⊥AC于点F,且DE=BF,则图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
2题图 3题图 4题图 5题图
3.如图,已知AB=AD,那么添加下列哪一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
4.如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.AC=AD B.AB=AB C.∠ABC=∠ABD D.∠BAC=∠BAD
5.如图,小敏用三角尺按下面方法画角平分线:在已知的∠AOB的两边上,分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,画射线OP,则OP平分∠AOB,其作图原理是:△OMP≌△ONP,这样就有∠AOP=∠BOP,则说明这两个三角形全等的依据是( )
A.SAS B.ASA C.AAS D.HL
6.如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE与CD相交于O,且∠1=∠2,则下列结论正确的个数为( )
①∠B=∠C;②△ADO≌△AEO;③△BOD≌△COE;④图中有四组三角形全等.
A.1个 B.2个 C.3个 D.4个
6题图 7题图 8题图 9题图 10题图
7.如图,AD⊥DC,AB⊥BC,若AB=AD,∠DAB=120°,则∠ACB的度数为( )
A.30° B.45° C.60° D.75°
8.如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面的两个木桩上,两个木桩离旗杆底部的距离BD与CD间的关系是( )
A.BD>CD B.BD
A.1 B.1或3 C.1或7 D.3或7
10.如图,已知∠E=∠F=90°,∠B=∠C,AE=AF,下列结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题
11.如图,已知方格纸中是4个相同的正方形,则∠1+∠3=_______.
11题图 12题图 13题图 14题图
12.如图,在△ABC中,∠C=90°,DE⊥AB于E,BE=BC,如果AC=6,那么AD+DE等于____.
13.如图,要测量河岸相对的两点A,B之间的距离,先从点B处出发与AB成90°角方向,向前走50米到点C处立一根标杆,然后方向不变继续朝前走50米到点D处,在点D处转90°沿DE方向再走17米,到达点E处,使点A,C,E在一条直线上,那么测得点A,B的距离为______米.
14.如图,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,下面四个结论:①∠ABE=∠BAD;②△CEB≌△ADC;③AB=CE;④AD-BE=DE.其中正确的是________.(将你认为正确的序号都写上)
15.如图,MN∥PQ,AB⊥PQ,点A,D在直线MN上,点B,C在直线PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB=______.
15题图 16题图 17题图 18题图
16.如图,在△ABC中,∠C=90°,DE⊥AB于点E,BE=BC,如果AC=6,则AD+DE=______.
17.如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=_______.
18.如图,∠BAC=90°,AB=AC,过点A作直线DE,且作CE⊥ED,BD⊥ED,垂足分别为E,D.若CE=2,BD=6,则DE=____.
三.解答题
19.如图,点B,C,E,F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC=DF.求证:
(1)△ABC≌△DEF;
(2)AB∥DE.
20.如图,AD,BC相交于点O,AD=BC,∠C=∠D=90°.
(1)求证:△ACB≌△BDA;
(2)若∠ABC=35°,则∠CAO的度数是多少?
21.已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
(1)如图①,若点O在边BC上,求证:∠ABO=∠ACO;
(2)如图②,若点O在△ABC的内部,求证:∠ABO=∠ACO.
22. 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.求证:DE=AD-BE.
23.如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.(1)图中还有几对全等三角形?请你一一列举;(2)求证:CF=EF.
24.如图,已知A(-2,0),B(0,-4),C(1,1),点P为线段OB上一动点(不包括点O),CD⊥CP交x轴于点D,当P点运动时:
(1)求证:∠CPO=∠CDO;
(2)求证:CP=CD;
(3)下列两个结论:①AD-BP的值不变;②AD+BP的值不变.选择正确的结论并求其值.
参考答案
1-5 DCCAD 6-10DACCC
11.90°
12.6
17
①②④
7
16. 6
17.90°
18. 8
19. 解:(1)∵AC⊥BC于点C,DF⊥EF于点F,∴∠ACB=∠DFE=90°.
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS)
(2)由(1)可知△ABC≌△DEF,∴∠B=∠DEF,
∴AB∥DE
20. 解:(1)∵∠C=∠D=90°,
∴在Rt△ACB和Rt△BDA中
∴Rt△ACB≌Rt△BDA(HL)
(2)∵Rt△ABC≌Rt△BAD,∴∠ABC=∠BAD=35°,
∵∠C=90°,∴∠BAC=55°,
∴∠CAO=∠CAB-∠BAD=20°
21. 解:(1)过点O作OE⊥AB于E,作OF⊥AC于F,
则∠BEO=∠CFO=90°,
又∵OB=OC,OE=OF,∴Rt△BOE≌Rt△COF(HL),
∴∠ABO=∠ACO
(2)过点O分别作OE⊥AB,OF⊥AC,E,F分别是垂足,
则∠BEO=∠CFO=90°,
又∵OB=OC,OE=OF,∴Rt△BOE≌Rt△COF(HL),
∴∠ABO=∠ACO
22. 解:∵BE⊥CE,AD⊥CE,∴∠CEB=∠ADC=90°
又∵∠ACB=90°,∴∠BCE+∠ACD=90°, ∠ACDO+∠CAD=90°
∴∠BCE=∠ACDO
又∵AC=BC
∴△ACD≌△CBE(AAS),
∴AD=CE,BE=CD,
∵DE=CE-CD,∴DE=AD-BE
23. 解:(1)△ADC≌△ABE,△CDF≌△EBF
(2)连接AF,∵Rt△ABC≌Rt△ADE,
∴AB=AD,BC=DE,∠ABC=∠ADE=90°,
又∵AF=AF,∴Rt△ABF≌Rt△ADF(HL),
∴BF=DF,
又∵BC=DE,∴BC-BF=DE-DF,
即CF=EF
24. 解:(1)∵在△POK和△DCK中,∠C=∠POK=90°,∠OKP=∠DKC,
∴∠OPK=∠CDK,即∠CPO=∠CDO
(2)作CM⊥x轴于点M,CN⊥y轴于点N,易证△CMD≌△CNP(AAS),
∴CP=CD
(3)②正确,易证MD=NP,
∵AD=AO+OM+MD=3+MD,BP=NB-NP=NO+OB-NP=5-NP,
∴AD+BP=8
21世纪教育网(www.21cnjy.com)
