物理人教版(2019)必修第二册8.1.2功与功率 -变力做功(共22张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册8.1.2功与功率 -变力做功(共22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-27 06:04:11 | ||
图片预览




文档简介
(共22张PPT)
典例分析:
2.(练习册68页-2) 在水平桌面上用一个水平恒力F牵引木块运动,当速度达到vm后,立刻撤去力F,木块滑行一段距离直至停止,木块的v-t图像如图所示,则木块受到的牵引力F和所受的摩擦力f之比为 。全过程中F做的功W1和摩擦力做功的绝对值|W2|之比为 。
vm
O
1
2
3
4
t
v
拓展一:作用力和反作用力的功
S
N
S
N
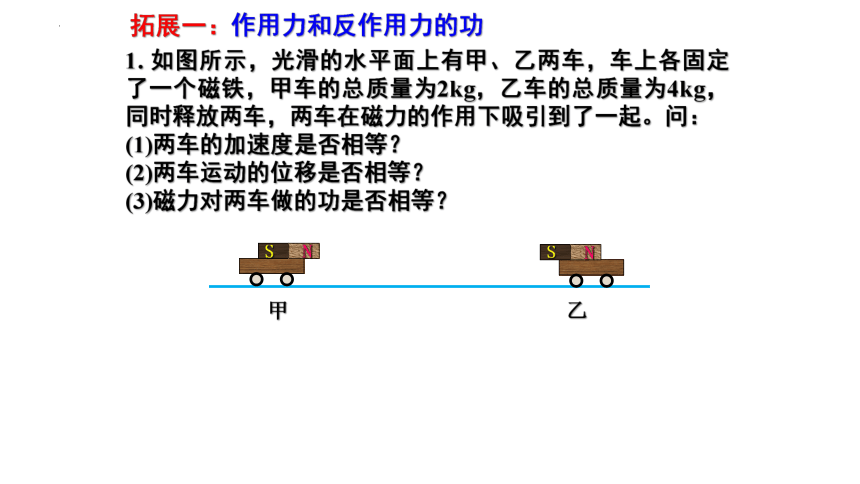
1. 如图所示,光滑的水平面上有甲、乙两车,车上各固定了一个磁铁,甲车的总质量为2kg,乙车的总质量为4kg,同时释放两车,两车在磁力的作用下吸引到了一起。问:
(1)两车的加速度是否相等?
(2)两车运动的位移是否相等?
(3)磁力对两车做的功是否相等?
甲
乙
拓展一:作用力和反作用力的功
S
N
S
N
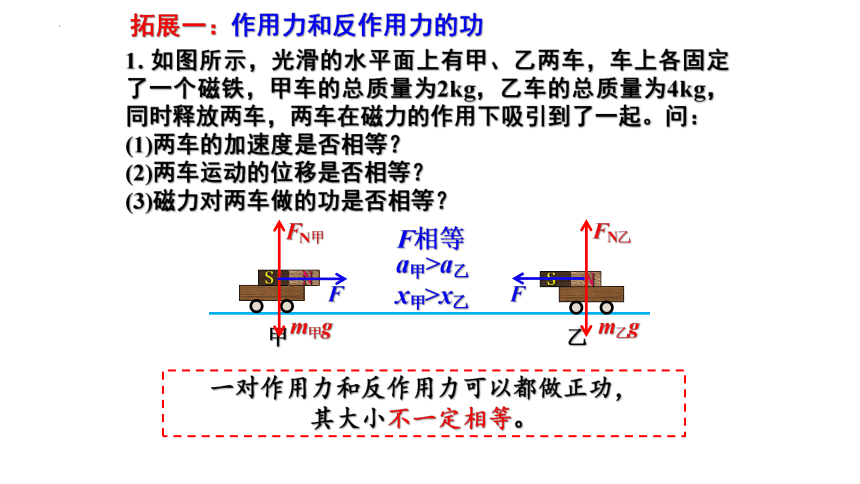
1. 如图所示,光滑的水平面上有甲、乙两车,车上各固定了一个磁铁,甲车的总质量为2kg,乙车的总质量为4kg,同时释放两车,两车在磁力的作用下吸引到了一起。问:
(1)两车的加速度是否相等?
(2)两车运动的位移是否相等?
(3)磁力对两车做的功是否相等?
甲
乙
一对作用力和反作用力可以都做正功,
其大小不一定相等。
m甲g
FN甲
F
m乙g
FN乙
F
F相等
a甲>a乙
x甲>x乙
拓展一:作用力和反作用力的功
2. 如图所示,质量为m的物块在动摩擦因数为μ的桌面上向右滑动了L。求:滑动摩擦力对物块和桌面各做了多少功?
v0
L
f
f
做负功
不做功
-μmgL
3. 如图所示,质量为M的小车放在光滑水平面上,质量为m的物块以一定的初速度v0滑上小车左端,两者间的动摩擦因数为μ。求:滑动摩擦力对物块和小车各做了多少功?
LM
Lm
M
v0
m
M
m
f
f
做负功
-μmgLm
做正功
μmgLM
滑动摩擦力可以做负功、可以做正功、可以不做功
一对滑动摩擦力做功之和不一定于0
拓展一:作用力和反作用力的功
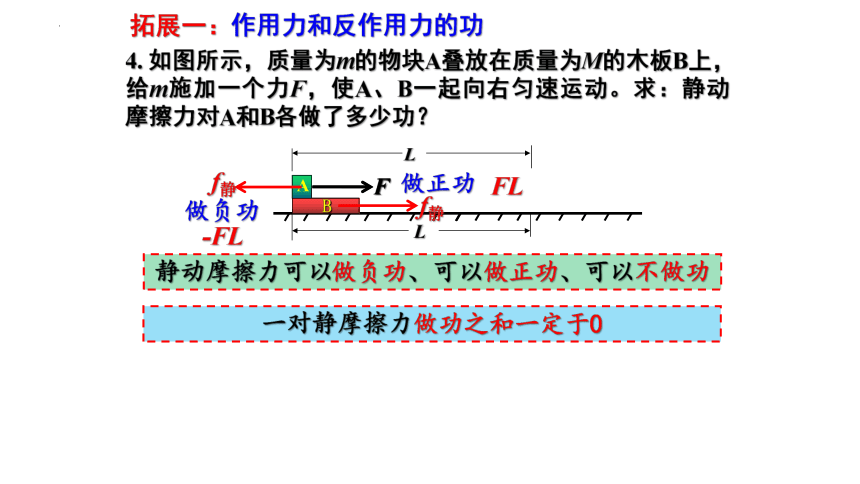
4. 如图所示,质量为m的物块A叠放在质量为M的木板B上,给m施加一个力F,使A、B一起向右匀速运动。求:静动摩擦力对A和B各做了多少功?
F
A
B
L
L
F
A
B
f静
f静
做负功
做正功
静动摩擦力可以做负功、可以做正功、可以不做功
-FL
FL
一对静摩擦力做功之和一定于0
典例分析:
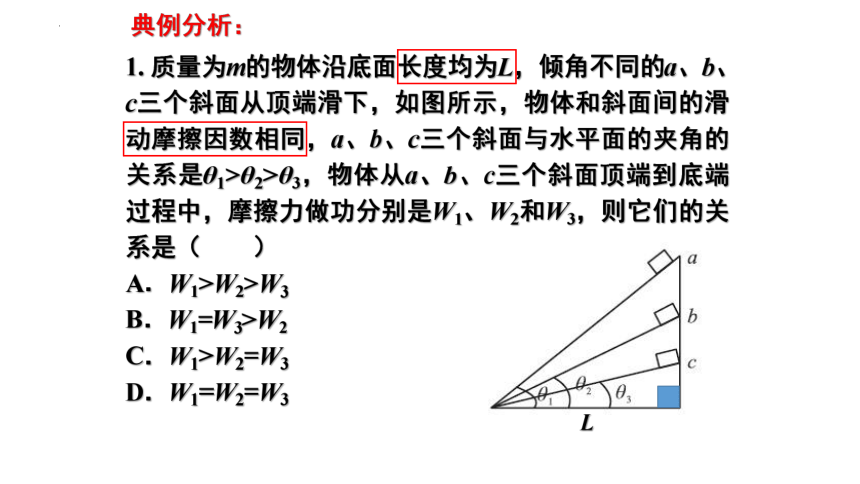
1. 质量为m的物体沿底面长度均为L,倾角不同的a、b、c三个斜面从顶端滑下,如图所示,物体和斜面间的滑动摩擦因数相同,a、b、c三个斜面与水平面的夹角的关系是θ1>θ2>θ3,物体从a、b、c三个斜面顶端到底端过程中,摩擦力做功分别是W1、W2和W3,则它们的关系是( )
A.W1>W2>W3
B.W1=W3>W2
C.W1>W2=W3
D.W1=W2=W3
L
变式训练: 质量为m的物体沿高度均为H,倾角不同的a、b、c三个斜面从顶端滑下,如图所示,物体和斜面间的滑动摩擦因数相同,a、b、c三个斜面与水平面的夹角的关系是θ1>θ2>θ3,物体从a、b、c三个斜面顶端到底端过程中,摩擦力做功分别是W1、W2和W3,则它们的关系是( )
A.W1>W2>W3
B.W1C.W1>W2=W3
D.W1=W2=W3
θ1
θ2
θ3
H
a
b
c
中物理
第八章 机械能守恒定律
专题1: 变力做功
功的计算公式W=Flcos α只适用于恒力做功的情况,对于变力做功的计算是学习的难点,也是重点。我们有哪些方法可以解决变力做功的问题呢?或者说我们能不能把变力转化成恒力来处理呢?
课堂引入
现结合例题将变力做功的四种解法(除动能定理外)总结如下:
方法一:平均值法
2.平均值法:如果物体受到的力是随着位移均匀变化的,则可以利用用公式 求变力做功,物体受到的平均力的大小 ,其中F1为物体初状态时受到的力,F2为物体末状态时受到的力.
1.分段法:力在全程是变力,但在每一个阶段是恒力,这样就可以先计算每个阶段做的功,再利用求和的方法计算整个过程中变力做的功。
方法一:平均值法
【典例2】如图所示,放在水平地面上的木块与一劲度系数k=200 N/m的轻质弹簧相连,现用手水平拉弹簧,拉力的作用点移动x1=0.2 m,木块开始运动,继续拉弹簧,木块缓慢移动了x2=0.4 m,求上述过程中拉力所做的功.
方法二:平均值法
方法二:平均值法
方法二:图像法
在F x图象中,图线与x轴所围的“面积”的代数和表示F做的功.“面积”有正负,在x轴上方的“面积”为正,在x轴下方的“面积”为负.如图甲、乙所示,这与运动学中由v t图象求位移的原理相同.
方法二:图像法
【例题3】一个物体所受的力F随位移l变化的图像如图所示,在这一过程中,力F对物体做的功为( )
A.3 J B.6 J C.7 J D.8 J
【解析】力F对物体做的功等于l轴上方梯形“面积”所表示的正功与l轴下方三角形“面积”所表示的负功的代数和。W1= ×(3+4)×2 J=7 J,
W2=- ×(5-4)×2 J=-1 J,所以力F对物体做的功为W=7 J-1 J=6 J,选项B正确。
【正确答案】B
【变式3】用质量为5 kg的均匀铁索,从10 m深的井中吊起一质量为20 kg的物体,此过程中人的拉力随物体上升的高度变化如图所示,在这个过程中人至少要做多少功?(g取10 m/s2)
方法二:图像法
方法三:微元法
当力的大小不变,力的方向时刻与速度同向(或反向)时,把物体的运动过程分为很多小段,这样每一小段可以看成直线,先求力在每一小段上做的功,再求和即可。
例如,滑动摩擦力、空气阻力总与物体相对运动的方向相反,可把运动过程细分,其中每一小段都是恒力做功,整个运动过程中所做的总功是各个阶段所做功的和,即力与路程的乘积。
方法三:微元法
【典例4】如图所示,质量为m的质点在力F的作用下,沿水平面上半径为R的光滑圆槽运动一周.若F的大小不变,方向始终与圆槽相切(与速度的方向相同),求力F对质点做的功.
【解析】质点在运动的过程中,F的方向始终与速度的方向相同,若将圆周分成许多极短的小圆弧Δl1、Δl2、Δl3、…、Δln,则每段小圆弧都可以看成一段极短的直线,所以质点运动一周,力F对质点做的功等于它在每一小段上做功的代数和,即W=W1+W2+…+Wn=F(Δl1+Δl2+…+Δln)=2πRF.
【答案】 2πRF
方法三:微元法
【变式4】在水平面上,有一弯曲的槽道AB,槽道由半径分别为 和R的两个半圆构成。如图所示,现用大小恒为F的拉力将一光滑小球从A点沿槽道拉至B点,若拉力F的方向时刻均与小球运动方向一致,则此过程中拉力所做的功为( )
A.0 B.FR C. D.2πFR
【典例1】如图,用恒力F通过跨过光滑定滑轮的轻绳,将静止于水平面上的物体从位置A拉到位置B,物体和滑轮的大小均忽略,定滑轮距水平面高为h,物体在位置A、B时,细绳与水平面的夹角分别为α和β,求绳的拉力F对物体做的功.
h
【分析】功是能量转化的量度,轻绳不存储能量,恒力F做功通过绳子将能量转移到物体上,故此恒力F做功应该等于绳子对物体做的功。
方法四:等效转化法
A
B
【变式1】人在A点拉着绳通过一个光滑定滑轮以加速度a匀加速吊起质量为m的物体,如图所示,保持人手与滑轮间的距离不变,大小为h,开始时绳与水平方向成 600 角,当人拉着绳由A点沿水平方向运动到B点时,绳与水平方向成300 角,求人对绳的拉力做了多少功?(不计摩擦)
方法一:等效转化法
h
课堂小结
THANKS
“
”
典例分析:
2.(练习册68页-2) 在水平桌面上用一个水平恒力F牵引木块运动,当速度达到vm后,立刻撤去力F,木块滑行一段距离直至停止,木块的v-t图像如图所示,则木块受到的牵引力F和所受的摩擦力f之比为 。全过程中F做的功W1和摩擦力做功的绝对值|W2|之比为 。
vm
O
1
2
3
4
t
v
拓展一:作用力和反作用力的功
S
N
S
N
1. 如图所示,光滑的水平面上有甲、乙两车,车上各固定了一个磁铁,甲车的总质量为2kg,乙车的总质量为4kg,同时释放两车,两车在磁力的作用下吸引到了一起。问:
(1)两车的加速度是否相等?
(2)两车运动的位移是否相等?
(3)磁力对两车做的功是否相等?
甲
乙
拓展一:作用力和反作用力的功
S
N
S
N
1. 如图所示,光滑的水平面上有甲、乙两车,车上各固定了一个磁铁,甲车的总质量为2kg,乙车的总质量为4kg,同时释放两车,两车在磁力的作用下吸引到了一起。问:
(1)两车的加速度是否相等?
(2)两车运动的位移是否相等?
(3)磁力对两车做的功是否相等?
甲
乙
一对作用力和反作用力可以都做正功,
其大小不一定相等。
m甲g
FN甲
F
m乙g
FN乙
F
F相等
a甲>a乙
x甲>x乙
拓展一:作用力和反作用力的功
2. 如图所示,质量为m的物块在动摩擦因数为μ的桌面上向右滑动了L。求:滑动摩擦力对物块和桌面各做了多少功?
v0
L
f
f
做负功
不做功
-μmgL
3. 如图所示,质量为M的小车放在光滑水平面上,质量为m的物块以一定的初速度v0滑上小车左端,两者间的动摩擦因数为μ。求:滑动摩擦力对物块和小车各做了多少功?
LM
Lm
M
v0
m
M
m
f
f
做负功
-μmgLm
做正功
μmgLM
滑动摩擦力可以做负功、可以做正功、可以不做功
一对滑动摩擦力做功之和不一定于0
拓展一:作用力和反作用力的功
4. 如图所示,质量为m的物块A叠放在质量为M的木板B上,给m施加一个力F,使A、B一起向右匀速运动。求:静动摩擦力对A和B各做了多少功?
F
A
B
L
L
F
A
B
f静
f静
做负功
做正功
静动摩擦力可以做负功、可以做正功、可以不做功
-FL
FL
一对静摩擦力做功之和一定于0
典例分析:
1. 质量为m的物体沿底面长度均为L,倾角不同的a、b、c三个斜面从顶端滑下,如图所示,物体和斜面间的滑动摩擦因数相同,a、b、c三个斜面与水平面的夹角的关系是θ1>θ2>θ3,物体从a、b、c三个斜面顶端到底端过程中,摩擦力做功分别是W1、W2和W3,则它们的关系是( )
A.W1>W2>W3
B.W1=W3>W2
C.W1>W2=W3
D.W1=W2=W3
L
变式训练: 质量为m的物体沿高度均为H,倾角不同的a、b、c三个斜面从顶端滑下,如图所示,物体和斜面间的滑动摩擦因数相同,a、b、c三个斜面与水平面的夹角的关系是θ1>θ2>θ3,物体从a、b、c三个斜面顶端到底端过程中,摩擦力做功分别是W1、W2和W3,则它们的关系是( )
A.W1>W2>W3
B.W1
D.W1=W2=W3
θ1
θ2
θ3
H
a
b
c
中物理
第八章 机械能守恒定律
专题1: 变力做功
功的计算公式W=Flcos α只适用于恒力做功的情况,对于变力做功的计算是学习的难点,也是重点。我们有哪些方法可以解决变力做功的问题呢?或者说我们能不能把变力转化成恒力来处理呢?
课堂引入
现结合例题将变力做功的四种解法(除动能定理外)总结如下:
方法一:平均值法
2.平均值法:如果物体受到的力是随着位移均匀变化的,则可以利用用公式 求变力做功,物体受到的平均力的大小 ,其中F1为物体初状态时受到的力,F2为物体末状态时受到的力.
1.分段法:力在全程是变力,但在每一个阶段是恒力,这样就可以先计算每个阶段做的功,再利用求和的方法计算整个过程中变力做的功。
方法一:平均值法
【典例2】如图所示,放在水平地面上的木块与一劲度系数k=200 N/m的轻质弹簧相连,现用手水平拉弹簧,拉力的作用点移动x1=0.2 m,木块开始运动,继续拉弹簧,木块缓慢移动了x2=0.4 m,求上述过程中拉力所做的功.
方法二:平均值法
方法二:平均值法
方法二:图像法
在F x图象中,图线与x轴所围的“面积”的代数和表示F做的功.“面积”有正负,在x轴上方的“面积”为正,在x轴下方的“面积”为负.如图甲、乙所示,这与运动学中由v t图象求位移的原理相同.
方法二:图像法
【例题3】一个物体所受的力F随位移l变化的图像如图所示,在这一过程中,力F对物体做的功为( )
A.3 J B.6 J C.7 J D.8 J
【解析】力F对物体做的功等于l轴上方梯形“面积”所表示的正功与l轴下方三角形“面积”所表示的负功的代数和。W1= ×(3+4)×2 J=7 J,
W2=- ×(5-4)×2 J=-1 J,所以力F对物体做的功为W=7 J-1 J=6 J,选项B正确。
【正确答案】B
【变式3】用质量为5 kg的均匀铁索,从10 m深的井中吊起一质量为20 kg的物体,此过程中人的拉力随物体上升的高度变化如图所示,在这个过程中人至少要做多少功?(g取10 m/s2)
方法二:图像法
方法三:微元法
当力的大小不变,力的方向时刻与速度同向(或反向)时,把物体的运动过程分为很多小段,这样每一小段可以看成直线,先求力在每一小段上做的功,再求和即可。
例如,滑动摩擦力、空气阻力总与物体相对运动的方向相反,可把运动过程细分,其中每一小段都是恒力做功,整个运动过程中所做的总功是各个阶段所做功的和,即力与路程的乘积。
方法三:微元法
【典例4】如图所示,质量为m的质点在力F的作用下,沿水平面上半径为R的光滑圆槽运动一周.若F的大小不变,方向始终与圆槽相切(与速度的方向相同),求力F对质点做的功.
【解析】质点在运动的过程中,F的方向始终与速度的方向相同,若将圆周分成许多极短的小圆弧Δl1、Δl2、Δl3、…、Δln,则每段小圆弧都可以看成一段极短的直线,所以质点运动一周,力F对质点做的功等于它在每一小段上做功的代数和,即W=W1+W2+…+Wn=F(Δl1+Δl2+…+Δln)=2πRF.
【答案】 2πRF
方法三:微元法
【变式4】在水平面上,有一弯曲的槽道AB,槽道由半径分别为 和R的两个半圆构成。如图所示,现用大小恒为F的拉力将一光滑小球从A点沿槽道拉至B点,若拉力F的方向时刻均与小球运动方向一致,则此过程中拉力所做的功为( )
A.0 B.FR C. D.2πFR
【典例1】如图,用恒力F通过跨过光滑定滑轮的轻绳,将静止于水平面上的物体从位置A拉到位置B,物体和滑轮的大小均忽略,定滑轮距水平面高为h,物体在位置A、B时,细绳与水平面的夹角分别为α和β,求绳的拉力F对物体做的功.
h
【分析】功是能量转化的量度,轻绳不存储能量,恒力F做功通过绳子将能量转移到物体上,故此恒力F做功应该等于绳子对物体做的功。
方法四:等效转化法
A
B
【变式1】人在A点拉着绳通过一个光滑定滑轮以加速度a匀加速吊起质量为m的物体,如图所示,保持人手与滑轮间的距离不变,大小为h,开始时绳与水平方向成 600 角,当人拉着绳由A点沿水平方向运动到B点时,绳与水平方向成300 角,求人对绳的拉力做了多少功?(不计摩擦)
方法一:等效转化法
h
课堂小结
THANKS
“
”
