高中数学人教新课标B版必修3--《2.1.3 分层抽样》课件3(共18张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修3--《2.1.3 分层抽样》课件3(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 597.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-26 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
2.1.3分层抽样
提问回顾
总体的个数较少时采用简单随机抽样
总体的个数较多时采用系统抽样
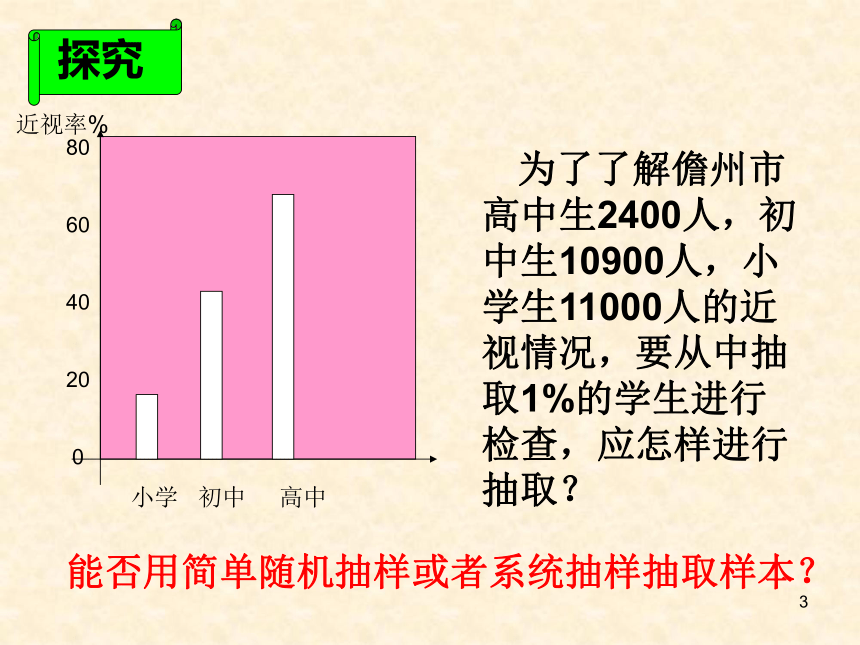
为了了解儋州市高中生2400人,初中生10900人,小学生11000人的近视情况,要从中抽取1%的学生进行检查,应怎样进行抽取?
80
60
40
20
0
近视率%
小学 初中 高中
能否用简单随机抽样或者系统抽样抽取样本?
*
探究
探究: 为了了解儋州市高中生2400人,初中生10900人,小学生11000人.此地区教育部门为了了解本地区中小学生的近视情况及其形成原因,要从本地区的中小学生中抽取1%的学生进行调查,你认为应当怎样抽取样本
(1)哪些因素可能会影响学生视力?
探究新知
视力可能受年龄阶段的影响
有差异,抽样时应该要考虑年龄阶段的不同
(3)总体有什么特点?用系统抽样会出现什么样的情况?
总体由差异明显的几部分组成,用系统抽样数据代表性不好。
分析:
探究: 为了了解儋州市高中生2400人,初中生10900人,小学生11000人.此地区教育部门为了了解本地区中小学生的近视情况及其形成原因,要从本地区的中小学生中抽取1%的学生进行调查,你认为应当怎样抽取样本
分析:
探究新知
(5)如何确定各学段所要抽取的人数?样本容量怎么形成?
(4)应如何提高样本的代表性?能否在 三个学段中平均抽取?
应考虑他们在样本中所占的比例。
按比例分配人数到各个阶段,得到各个学段所要抽取的个体数,再把各阶段抽取个数合在一起。
因为总体由差异明显的三个部分组成,所以按比例分配人数到各个部分。
高中生人数:2400×1%=24( 人)
初中生人数:10900×1%=109(人)
小学生人数: 11000×1%=110(人)
解:
探究1:为了了解儋州市高中生2400人,初中生10900人,小学生11000人.此地区教育部门为了了解本地区中小学生的近视情况及其形成原因,要从本地区的中小学生中抽取1%的学生进行调查,你认为应当怎样抽取样本
分层抽样
一般地,在抽样时,将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,将各层取出的个体合在一起作为样本,这种抽样方法是分层抽样。
探究新知
(2)比例:分层抽样为保证每个个体等可能入样,这样可以保证样本结构与总体结构的一致性,从而提高了样本的代表性;
(3)各层独立地抽取:在分层抽样中,每一层内部都要独立地进行抽样,并且为了确保抽样的随机性,各层应分别按简单随机抽样或系统抽样的方法抽取,因此,分层抽样也是一种等概率抽样.
例 1 某单位有500名职工,其中不到35岁的有125人,35~49岁的有280人,50岁以上的有95人.为了了解该单位职工年龄与身体状况的有关指标,从中抽取100名职工作为样本,应该怎样抽取?你能说出抽样过程吗?
*
新知初用
例 1 某单位有500名职工,其中不到35岁的有125人,35~49岁的有280人,50岁以上的有95人.为了了解该单位职工年龄与身体状况的有关指标,从中抽取100名职工作为样本,应该怎样抽取?
*
(2)确定样本容量与总体的个体数之比100:500=1:5;
(3)利用抽样比确定各年龄段应抽取的个体数:
不到35岁的职工:125× =25(人)
35~49岁的职工:280× =56(人)
50岁以上的职工:95× =19(人)
(4)利用简单随机抽样或系统抽样的方法,从各年龄段分别抽取25,56,19人;
(5)然后将抽取的25,56,19人合在一起,就是所抽取的样本.
分层
定比
定量
抽样
组样
某单位有501名职工,其中不到35岁的有126人,35~49岁的有280人,50岁以上的有95人.为了了解该单位职工年龄与身体状况的有关指标,从中抽取总体的五分之一职工作为样本,应该怎样抽取?
*
例1变形
问题1: 如何确定每层的样本数?
问题2 :实际抽样过程中遇到什么问题?
分层抽样时,若某层中按抽样比算不是整数时,则需先剔除几个个体,在剔除时要随机剔除以保证每个个体被抽取的机会相等.
变形 某单位有501名职工,其中不到35岁的有126人,35~49岁的有280人,50岁以上的有95人.为了了解该单位职工年龄与身体状况的有关指标,从中抽取总体的五分之一名职工作为样本,应该怎样抽取?
*
(2)抽样比为五分之一
(3)在不到35岁的有126人用简单随机抽样随机剔除1人后确定
不到35岁的职工:125× =25(人)
35~49岁的职工:280× =56(人)
50岁以上的职工:95× =19(人)
(4)利用简单随机抽样或系统抽样的方法,从各年龄段分别抽取25,56,19人;
(5)然后将抽取的25,56,19人合在一起,就是所抽取的样本.
分层
定比
定量
抽样
组样
2 分层抽样的步骤:
(1) 将总体按一定的标准分层;
(2)确定抽样比;
(3) 确定各层抽取的样本数;
(5)综合每层抽样,组成样本。
(4)在每一层进行抽样(可用简单
随机抽样或系统抽样);
开始
分层
定比
定量
抽样
组样
结束
巩固深化
注意:分层抽样时,若某层中按抽样比算不是整数时,则需先剔除几个个体.
现场做一个调查,利用分层抽样抽取五分之一名同学的身高作为样本来调查班级52同学(其中男生32名,女生20名)的平均身高.
小试身手
简单随机抽样、系统抽样、分层抽样的特点
简单随机抽样:
①总体容量较小;
②逐个抽取
不放回抽取;
系统抽样:
①总体容量较大;
②分段,按规定的间隔在各部分抽取;
③每个个体被抽到的机会相等.
知识整合
③每个个体被抽到的机会相等
1、下列问题中,采用怎样的抽样方法比较合理:
①从10台冰箱中抽取3台进行质量检查;
②某电影院有32排座位,每排有40个座位,座位号为1~40。 有一次报告会坐满了听众,会议结束后为听取意见,留下座位号为18的32名听众进行座谈;
③某学校有160名教职工,其中教师120名,行政人员16名,后勤人员24名。为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本。
③分层抽样
②系统抽样
①简单随机抽样
巩固练习
2、某单位有老年人21人,中年人30人,青年人50人,为了调查他们的身体情况,需从他们中抽取十分之一作为样本,则适合的抽取方法是 ( )
A.简单随机抽样 B.系统抽样 C.分层抽样
D.先从老人中剔除1人,然后再分层抽样
*
巩固练习
巩固练习
D
小结
(1)知识内容
●分层抽样的定义
●分层抽样的步骤
分层、定比、定量、抽样、组样
●恰当的选择三种抽样方法解决生活中的抽样问题
(1)必做题:教材 习题2.1 A组 第5题
(2)探究题:分别用简单随机抽样、系统抽样和分层抽样的方法,从全班52名同学中抽取10名同学,统计他们的平均身高.全面调查全班同学的平均身高,并与抽样统计的结果进行比较,你能发现什么问题?
布置作业
2.1.3分层抽样
提问回顾
总体的个数较少时采用简单随机抽样
总体的个数较多时采用系统抽样
为了了解儋州市高中生2400人,初中生10900人,小学生11000人的近视情况,要从中抽取1%的学生进行检查,应怎样进行抽取?
80
60
40
20
0
近视率%
小学 初中 高中
能否用简单随机抽样或者系统抽样抽取样本?
*
探究
探究: 为了了解儋州市高中生2400人,初中生10900人,小学生11000人.此地区教育部门为了了解本地区中小学生的近视情况及其形成原因,要从本地区的中小学生中抽取1%的学生进行调查,你认为应当怎样抽取样本
(1)哪些因素可能会影响学生视力?
探究新知
视力可能受年龄阶段的影响
有差异,抽样时应该要考虑年龄阶段的不同
(3)总体有什么特点?用系统抽样会出现什么样的情况?
总体由差异明显的几部分组成,用系统抽样数据代表性不好。
分析:
探究: 为了了解儋州市高中生2400人,初中生10900人,小学生11000人.此地区教育部门为了了解本地区中小学生的近视情况及其形成原因,要从本地区的中小学生中抽取1%的学生进行调查,你认为应当怎样抽取样本
分析:
探究新知
(5)如何确定各学段所要抽取的人数?样本容量怎么形成?
(4)应如何提高样本的代表性?能否在 三个学段中平均抽取?
应考虑他们在样本中所占的比例。
按比例分配人数到各个阶段,得到各个学段所要抽取的个体数,再把各阶段抽取个数合在一起。
因为总体由差异明显的三个部分组成,所以按比例分配人数到各个部分。
高中生人数:2400×1%=24( 人)
初中生人数:10900×1%=109(人)
小学生人数: 11000×1%=110(人)
解:
探究1:为了了解儋州市高中生2400人,初中生10900人,小学生11000人.此地区教育部门为了了解本地区中小学生的近视情况及其形成原因,要从本地区的中小学生中抽取1%的学生进行调查,你认为应当怎样抽取样本
分层抽样
一般地,在抽样时,将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,将各层取出的个体合在一起作为样本,这种抽样方法是分层抽样。
探究新知
(2)比例:分层抽样为保证每个个体等可能入样,这样可以保证样本结构与总体结构的一致性,从而提高了样本的代表性;
(3)各层独立地抽取:在分层抽样中,每一层内部都要独立地进行抽样,并且为了确保抽样的随机性,各层应分别按简单随机抽样或系统抽样的方法抽取,因此,分层抽样也是一种等概率抽样.
例 1 某单位有500名职工,其中不到35岁的有125人,35~49岁的有280人,50岁以上的有95人.为了了解该单位职工年龄与身体状况的有关指标,从中抽取100名职工作为样本,应该怎样抽取?你能说出抽样过程吗?
*
新知初用
例 1 某单位有500名职工,其中不到35岁的有125人,35~49岁的有280人,50岁以上的有95人.为了了解该单位职工年龄与身体状况的有关指标,从中抽取100名职工作为样本,应该怎样抽取?
*
(2)确定样本容量与总体的个体数之比100:500=1:5;
(3)利用抽样比确定各年龄段应抽取的个体数:
不到35岁的职工:125× =25(人)
35~49岁的职工:280× =56(人)
50岁以上的职工:95× =19(人)
(4)利用简单随机抽样或系统抽样的方法,从各年龄段分别抽取25,56,19人;
(5)然后将抽取的25,56,19人合在一起,就是所抽取的样本.
分层
定比
定量
抽样
组样
某单位有501名职工,其中不到35岁的有126人,35~49岁的有280人,50岁以上的有95人.为了了解该单位职工年龄与身体状况的有关指标,从中抽取总体的五分之一职工作为样本,应该怎样抽取?
*
例1变形
问题1: 如何确定每层的样本数?
问题2 :实际抽样过程中遇到什么问题?
分层抽样时,若某层中按抽样比算不是整数时,则需先剔除几个个体,在剔除时要随机剔除以保证每个个体被抽取的机会相等.
变形 某单位有501名职工,其中不到35岁的有126人,35~49岁的有280人,50岁以上的有95人.为了了解该单位职工年龄与身体状况的有关指标,从中抽取总体的五分之一名职工作为样本,应该怎样抽取?
*
(2)抽样比为五分之一
(3)在不到35岁的有126人用简单随机抽样随机剔除1人后确定
不到35岁的职工:125× =25(人)
35~49岁的职工:280× =56(人)
50岁以上的职工:95× =19(人)
(4)利用简单随机抽样或系统抽样的方法,从各年龄段分别抽取25,56,19人;
(5)然后将抽取的25,56,19人合在一起,就是所抽取的样本.
分层
定比
定量
抽样
组样
2 分层抽样的步骤:
(1) 将总体按一定的标准分层;
(2)确定抽样比;
(3) 确定各层抽取的样本数;
(5)综合每层抽样,组成样本。
(4)在每一层进行抽样(可用简单
随机抽样或系统抽样);
开始
分层
定比
定量
抽样
组样
结束
巩固深化
注意:分层抽样时,若某层中按抽样比算不是整数时,则需先剔除几个个体.
现场做一个调查,利用分层抽样抽取五分之一名同学的身高作为样本来调查班级52同学(其中男生32名,女生20名)的平均身高.
小试身手
简单随机抽样、系统抽样、分层抽样的特点
简单随机抽样:
①总体容量较小;
②逐个抽取
不放回抽取;
系统抽样:
①总体容量较大;
②分段,按规定的间隔在各部分抽取;
③每个个体被抽到的机会相等.
知识整合
③每个个体被抽到的机会相等
1、下列问题中,采用怎样的抽样方法比较合理:
①从10台冰箱中抽取3台进行质量检查;
②某电影院有32排座位,每排有40个座位,座位号为1~40。 有一次报告会坐满了听众,会议结束后为听取意见,留下座位号为18的32名听众进行座谈;
③某学校有160名教职工,其中教师120名,行政人员16名,后勤人员24名。为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本。
③分层抽样
②系统抽样
①简单随机抽样
巩固练习
2、某单位有老年人21人,中年人30人,青年人50人,为了调查他们的身体情况,需从他们中抽取十分之一作为样本,则适合的抽取方法是 ( )
A.简单随机抽样 B.系统抽样 C.分层抽样
D.先从老人中剔除1人,然后再分层抽样
*
巩固练习
巩固练习
D
小结
(1)知识内容
●分层抽样的定义
●分层抽样的步骤
分层、定比、定量、抽样、组样
●恰当的选择三种抽样方法解决生活中的抽样问题
(1)必做题:教材 习题2.1 A组 第5题
(2)探究题:分别用简单随机抽样、系统抽样和分层抽样的方法,从全班52名同学中抽取10名同学,统计他们的平均身高.全面调查全班同学的平均身高,并与抽样统计的结果进行比较,你能发现什么问题?
布置作业
