高中数学人教新课标B版必修3--《2.2.2 用样本的数字特征估计总体的数字特征》课件3(共26张PPT)
文档属性
| 名称 | 高中数学人教新课标B版必修3--《2.2.2 用样本的数字特征估计总体的数字特征》课件3(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 849.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-26 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
2.2.2 用样本的数字特征估计总体的数字特征(1)
思考:在初中我们学过众数、中位数 和平均数的概念,这些数据都是反映样本 信息的数字特征,对一组样本数据如何求
众数、中位数和平均数?
1.众 数
2.中位数
3.平均数
在一组数据中,出现次数最多的
数据叫做这一组数据的众数。
将一组数据按大小依次排列,把处在最中间位置的一个数据(或两个数据的平均数)叫做这组数据的中位数。
一组数据的总和除以数据的个数
所得的值。
一、知识链接
众数、中位数、平均数的计算
【常考题型】
探究
“用数据说话”,这是我们经常可以听 到的一句话,但是数据有时候也会被利用,从 而产生误导,你认为“我们单位的收入水平比
别的单位高”这句话应当怎么解释?
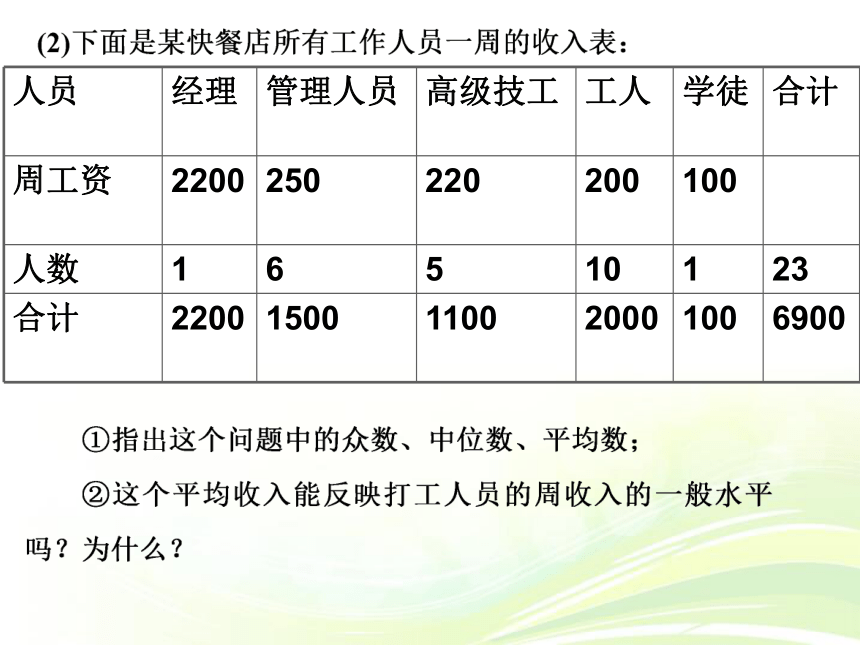
人员 经理 管理人员 高级技工 工人 学徒 合计
周工资 2200 250 220 200 100
人数 1 6 5 10 1 23
合计 2200 1500 1100 2000 100 6900
分析:众数为200,中位数为220,平均数为300。
因平均数为300,由表格中所列出的数据可见,只有经理在平均数以上,其余的人都在平均数以下,故用平均数不能客观真实地反映该工厂的工资水平。
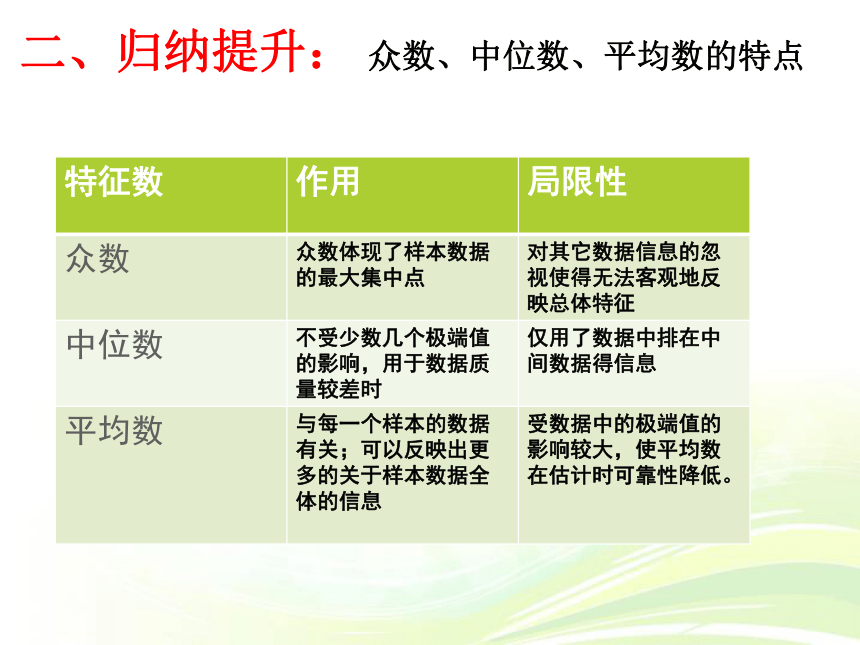
二、归纳提升: 众数、中位数、平均数的特点
特征数 作用 局限性
众数 众数体现了样本数据的最大集中点 对其它数据信息的忽视使得无法客观地反映总体特征
中位数 不受少数几个极端值的影响,用于数据质量较差时 仅用了数据中排在中间数据得信息
平均数 与每一个样本的数据有关;可以反映出更多的关于样本数据全体的信息
受数据中的极端值的影响较大,使平均数在估计时可靠性降低。
组距
组数
分组
频率分布表
作频率分布直方图的步骤
(4)列 .
(3)将数据 .
(1)求 .
(2)决定 与 .
极差
频率分布直方图
(5)画 .
知识链接
*
背景:为了提高全体学生体质健康水平,让更多的同学走进操场,走向阳光,积极参加体育锻炼,教育部决定从2007年开始,在全国范围内开展“全国亿万青少年学生阳光体育运动”,使大部分学生能做到每天锻炼一小时,于是一场学生体育锻炼的热潮被掀起了.请结合100名同学体育锻炼的现状探究:
(3)这组同学每周锻炼时间的平均水平如何?
(1)大部分人的每周锻炼时间集中在那个时段
(2)位于中间水平的每周锻炼时间又是多少?
三、新知探究: 众数、中位数、平均数与频率分布直方图的关系
*
*
*
问题1: 如何从频率分布直方图中估计众数?为什么?
取最高矩形下端中点的横坐标3.25作为众数.
1 众数:
在频率分布直方图中,就是最高矩形的中点的横坐标
*
*
1 众数:
在频率分布直方图中,就是最高矩形的中点的横坐标
在区间[3,3.5)的小长方形的面积最大,即这组的频率是最大的,也就是说锻炼时间在区间[3,3.5)内的同学最多,即众数就是在区间[3,3.5)内。
*
*
*
问题2: 如何从频率分布直方图中估计中位数,为什么?
前三个矩形的面积和=0.41
分析:在样本数据中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数,因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等。
总结:在频率分布直方图中,把频率分布直方图划分左右两个面积相等的分界线与x轴交点的横坐标称为中位数。
上图中,设中位数为x,则
后四个小矩形的面积和=0.48
4.91
2 中位数:左边和右边的直方图面积相等
0.25
0.15
0.09
0.11
0.13
0.22
0.06
0.10
*
问题3: 如何从频率分布直方图中估计平均数,为什么?
3 平均数
平均数的估计值等于每个小矩形的面积
乘以小矩形底边中点的横坐标之和
3.25×0.25+3.75×0.10+4.25×0.06+4.75×
0.11+5.25×0.13+5.75×0.15+6.25×0.09+
6.75×0.11=4.76(h).
3.25,3.75,4.25,4.75,5.25,
5.75,6.25,6.75,
*
*
0.25
0.15
0.09
0.11
0.13
0.22
0.06
0.10
从锻炼时间样本数据可知,该样本的众数是3.5,
中位数是4.75,平均数是4.825。这与我们从样本频率分布直方图得出的结论有偏差,你能解释一下原因吗?
因频率分布直方图本身得不出原始的数据内容,所以由频率分布直方图得到的众数、中位数平均值的估计往往与样本的实际中位数值不一致.
数字特征的综合应用
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
2.25
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
前四个小矩形的面积和=0.49
后四个小矩形的面积和=0.26
2.02
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
2.02
.
.
.
.
.
.
.
.
.
0.75
1.75
2.25
2.75
3.25
3.75
4.25
1.25
0.5
1.本节课你在数学知识和方法上有哪些收获?
2.你能从频率直方图中估计众数、中位数、平均数吗?
3.众数、中位数、平均数有哪些作用和局限性?
四、小结:
【练习反馈】
2.2.2 用样本的数字特征估计总体的数字特征(1)
思考:在初中我们学过众数、中位数 和平均数的概念,这些数据都是反映样本 信息的数字特征,对一组样本数据如何求
众数、中位数和平均数?
1.众 数
2.中位数
3.平均数
在一组数据中,出现次数最多的
数据叫做这一组数据的众数。
将一组数据按大小依次排列,把处在最中间位置的一个数据(或两个数据的平均数)叫做这组数据的中位数。
一组数据的总和除以数据的个数
所得的值。
一、知识链接
众数、中位数、平均数的计算
【常考题型】
探究
“用数据说话”,这是我们经常可以听 到的一句话,但是数据有时候也会被利用,从 而产生误导,你认为“我们单位的收入水平比
别的单位高”这句话应当怎么解释?
人员 经理 管理人员 高级技工 工人 学徒 合计
周工资 2200 250 220 200 100
人数 1 6 5 10 1 23
合计 2200 1500 1100 2000 100 6900
分析:众数为200,中位数为220,平均数为300。
因平均数为300,由表格中所列出的数据可见,只有经理在平均数以上,其余的人都在平均数以下,故用平均数不能客观真实地反映该工厂的工资水平。
二、归纳提升: 众数、中位数、平均数的特点
特征数 作用 局限性
众数 众数体现了样本数据的最大集中点 对其它数据信息的忽视使得无法客观地反映总体特征
中位数 不受少数几个极端值的影响,用于数据质量较差时 仅用了数据中排在中间数据得信息
平均数 与每一个样本的数据有关;可以反映出更多的关于样本数据全体的信息
受数据中的极端值的影响较大,使平均数在估计时可靠性降低。
组距
组数
分组
频率分布表
作频率分布直方图的步骤
(4)列 .
(3)将数据 .
(1)求 .
(2)决定 与 .
极差
频率分布直方图
(5)画 .
知识链接
*
背景:为了提高全体学生体质健康水平,让更多的同学走进操场,走向阳光,积极参加体育锻炼,教育部决定从2007年开始,在全国范围内开展“全国亿万青少年学生阳光体育运动”,使大部分学生能做到每天锻炼一小时,于是一场学生体育锻炼的热潮被掀起了.请结合100名同学体育锻炼的现状探究:
(3)这组同学每周锻炼时间的平均水平如何?
(1)大部分人的每周锻炼时间集中在那个时段
(2)位于中间水平的每周锻炼时间又是多少?
三、新知探究: 众数、中位数、平均数与频率分布直方图的关系
*
*
*
问题1: 如何从频率分布直方图中估计众数?为什么?
取最高矩形下端中点的横坐标3.25作为众数.
1 众数:
在频率分布直方图中,就是最高矩形的中点的横坐标
*
*
1 众数:
在频率分布直方图中,就是最高矩形的中点的横坐标
在区间[3,3.5)的小长方形的面积最大,即这组的频率是最大的,也就是说锻炼时间在区间[3,3.5)内的同学最多,即众数就是在区间[3,3.5)内。
*
*
*
问题2: 如何从频率分布直方图中估计中位数,为什么?
前三个矩形的面积和=0.41
分析:在样本数据中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数,因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等。
总结:在频率分布直方图中,把频率分布直方图划分左右两个面积相等的分界线与x轴交点的横坐标称为中位数。
上图中,设中位数为x,则
后四个小矩形的面积和=0.48
4.91
2 中位数:左边和右边的直方图面积相等
0.25
0.15
0.09
0.11
0.13
0.22
0.06
0.10
*
问题3: 如何从频率分布直方图中估计平均数,为什么?
3 平均数
平均数的估计值等于每个小矩形的面积
乘以小矩形底边中点的横坐标之和
3.25×0.25+3.75×0.10+4.25×0.06+4.75×
0.11+5.25×0.13+5.75×0.15+6.25×0.09+
6.75×0.11=4.76(h).
3.25,3.75,4.25,4.75,5.25,
5.75,6.25,6.75,
*
*
0.25
0.15
0.09
0.11
0.13
0.22
0.06
0.10
从锻炼时间样本数据可知,该样本的众数是3.5,
中位数是4.75,平均数是4.825。这与我们从样本频率分布直方图得出的结论有偏差,你能解释一下原因吗?
因频率分布直方图本身得不出原始的数据内容,所以由频率分布直方图得到的众数、中位数平均值的估计往往与样本的实际中位数值不一致.
数字特征的综合应用
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
2.25
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
前四个小矩形的面积和=0.49
后四个小矩形的面积和=0.26
2.02
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
2.02
.
.
.
.
.
.
.
.
.
0.75
1.75
2.25
2.75
3.25
3.75
4.25
1.25
0.5
1.本节课你在数学知识和方法上有哪些收获?
2.你能从频率直方图中估计众数、中位数、平均数吗?
3.众数、中位数、平均数有哪些作用和局限性?
四、小结:
【练习反馈】
